冀教版数学七年级下册 10.5 一元一次不等式组课件(共14张PPT)
文档属性
| 名称 | 冀教版数学七年级下册 10.5 一元一次不等式组课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-04 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
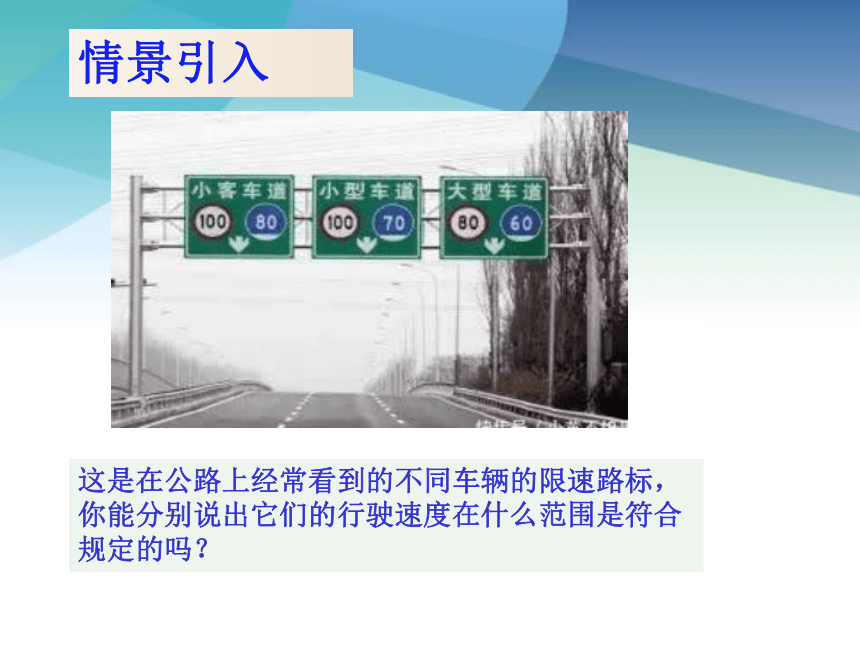
情景引入
这是在公路上经常看到的不同车辆的限速路标,你能分别说出它们的行驶速度在什么范围是符合规定的吗?
设小客车的速度为 X,有图可知
X≥80
X≤100
{
像上面这样,把两个或是两个以上不等式组成的一组不等式叫做不等式组
一起探究
同样的设小型车的速度为Y,可表示为
Y≥70
Y≤100
{
{
大型车的速度为Z,可以表示为
Z≥60
Z≤80
含有同一个未知数的一元一次不等式的不等式组叫一元一次不等式组.
类比方程组的概念,请同学们说一下一元一次不等式组的概念:
注意:一元一次不等式组需满足的3个条件:
(1)不等式必须是只含有同一个未知数
(2)每个不等式必须是一元一次不等式
(3)不等式的个数是两个或两个以上
概念学习:
X≥80
X≤100 这个不等式组中,只有一个未知数X,X表示的是小客车的速度,X的次数是1,这样的就是一元一次不等式组。
{
判断下列各式中哪些是一元一次不等式组?并说明理由
√
×
√
×
×
×
(7)-2-x<2X-7<2+3x
√
观察与思考
可知,小客车的速度x的范围是80≤x≤100.
不等式组 中, 和 的解集分别在数轴上表示,
X≥80
X≤100
{
80≤x≤100称为不等式组 的解集
X≥80
X≤100
{
60
120
80
100
一元一次不等式组中所有不等式的解集的公共部分,叫做这个一元一次不等式组的解集.
请同学们类比方程组的解,叙述一元一次不等式组的解集
概念学习
Y≥70
Y≤100
{
如:
不等式组
中,不等式 和 的解集分别表示在数轴上,如图,
70
80
90
100
110
60
公共部分为70≤Y≤100,所以不等式组的解集是:70≤Y≤100
–2 –1 0 1 2
–2 80 0 1 2
利用数轴确定不等式组的解集,你能发现有什么规律?
无解
–2 –1 0 1 2
-3
-2
-1
0
4
2
1
3
5
所以不等式组的解集是______。
(4)
(2)
(3)
(1)
所以不等式组的解集是_________。
所以不等式组的解集是______。
不等式组的解集是______。
分组探究:
-1<X<2
X<-1
a
b
a
b
设a < b
在数轴上表示解
不等式组的解集(规律口诀)
X>a
X>b
X<a
X<b
X>a
X<b
X<a
X>b
a
b
a
b
X>b
X<a
无解
a<X<b
大小小大中间找
大大小小找不到
同小取小
同大取大
一元一次不等式组的解集的规律
发现与归纳
解不等式组:
在数轴上表示不等式①,②的解集
所以这个不等式组的解集是x>3.
解不等式②,得
解:解不等式①,得
2x-1>x+1
X+8<4x-1
x>2.
x>3.
2
3
0
②
①
解一元一次不等式组步骤:
分别求出不等式组中每个不等式的解集
在数轴上表示出每个不等式的解集
找公共部分
写出不等式组的解集(注:找不到公共部分则不等式组无解)
运用巩固
解:解不等式①,得x≥ 8.
解不等式②,得 x< —
4
5
在数轴上表示不等式①,②的解集为
0
8
4
5
—
所以原不等式组无解.
①
②
解下列不等式组
练习提高:
(1)
(2)
①
②
解:解不等式①,得x<4
解不等式②,得x<2
在数轴上表示不等式
①,②的解集为
所以该不等式组的解集是x<2.
0 2 4
注意:在数轴上表示解集是空心点与实心点的区别
当堂检测
解下列不等式组
⑴
(2)
课堂小结:本节课中,我们……
学习了 概念
掌握了解 方法
体现了 数学思想
你还有哪些疑惑
请同学们写下来与小组的同学交流
一元一次不等式组
概念
一元一次不等式组的解
解一元一次不等式组
步骤方法
求出每个不等式的解集
在数轴上表示出每个解集
一元一次不等式组
确定各不等式解集的公共部分
写出一元一次不等式组的解集
数学思想
类比思想
数形结合思想
情景引入
这是在公路上经常看到的不同车辆的限速路标,你能分别说出它们的行驶速度在什么范围是符合规定的吗?
设小客车的速度为 X,有图可知
X≥80
X≤100
{
像上面这样,把两个或是两个以上不等式组成的一组不等式叫做不等式组
一起探究
同样的设小型车的速度为Y,可表示为
Y≥70
Y≤100
{
{
大型车的速度为Z,可以表示为
Z≥60
Z≤80
含有同一个未知数的一元一次不等式的不等式组叫一元一次不等式组.
类比方程组的概念,请同学们说一下一元一次不等式组的概念:
注意:一元一次不等式组需满足的3个条件:
(1)不等式必须是只含有同一个未知数
(2)每个不等式必须是一元一次不等式
(3)不等式的个数是两个或两个以上
概念学习:
X≥80
X≤100 这个不等式组中,只有一个未知数X,X表示的是小客车的速度,X的次数是1,这样的就是一元一次不等式组。
{
判断下列各式中哪些是一元一次不等式组?并说明理由
√
×
√
×
×
×
(7)-2-x<2X-7<2+3x
√
观察与思考
可知,小客车的速度x的范围是80≤x≤100.
不等式组 中, 和 的解集分别在数轴上表示,
X≥80
X≤100
{
80≤x≤100称为不等式组 的解集
X≥80
X≤100
{
60
120
80
100
一元一次不等式组中所有不等式的解集的公共部分,叫做这个一元一次不等式组的解集.
请同学们类比方程组的解,叙述一元一次不等式组的解集
概念学习
Y≥70
Y≤100
{
如:
不等式组
中,不等式 和 的解集分别表示在数轴上,如图,
70
80
90
100
110
60
公共部分为70≤Y≤100,所以不等式组的解集是:70≤Y≤100
–2 –1 0 1 2
–2 80 0 1 2
利用数轴确定不等式组的解集,你能发现有什么规律?
无解
–2 –1 0 1 2
-3
-2
-1
0
4
2
1
3
5
所以不等式组的解集是______。
(4)
(2)
(3)
(1)
所以不等式组的解集是_________。
所以不等式组的解集是______。
不等式组的解集是______。
分组探究:
-1<X<2
X<-1
a
b
a
b
设a < b
在数轴上表示解
不等式组的解集(规律口诀)
X>a
X>b
X<a
X<b
X>a
X<b
X<a
X>b
a
b
a
b
X>b
X<a
无解
a<X<b
大小小大中间找
大大小小找不到
同小取小
同大取大
一元一次不等式组的解集的规律
发现与归纳
解不等式组:
在数轴上表示不等式①,②的解集
所以这个不等式组的解集是x>3.
解不等式②,得
解:解不等式①,得
2x-1>x+1
X+8<4x-1
x>2.
x>3.
2
3
0
②
①
解一元一次不等式组步骤:
分别求出不等式组中每个不等式的解集
在数轴上表示出每个不等式的解集
找公共部分
写出不等式组的解集(注:找不到公共部分则不等式组无解)
运用巩固
解:解不等式①,得x≥ 8.
解不等式②,得 x< —
4
5
在数轴上表示不等式①,②的解集为
0
8
4
5
—
所以原不等式组无解.
①
②
解下列不等式组
练习提高:
(1)
(2)
①
②
解:解不等式①,得x<4
解不等式②,得x<2
在数轴上表示不等式
①,②的解集为
所以该不等式组的解集是x<2.
0 2 4
注意:在数轴上表示解集是空心点与实心点的区别
当堂检测
解下列不等式组
⑴
(2)
课堂小结:本节课中,我们……
学习了 概念
掌握了解 方法
体现了 数学思想
你还有哪些疑惑
请同学们写下来与小组的同学交流
一元一次不等式组
概念
一元一次不等式组的解
解一元一次不等式组
步骤方法
求出每个不等式的解集
在数轴上表示出每个解集
一元一次不等式组
确定各不等式解集的公共部分
写出一元一次不等式组的解集
数学思想
类比思想
数形结合思想
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
