第七章 平面直角坐标系 章末复习 课件(共34张PPT)
文档属性
| 名称 | 第七章 平面直角坐标系 章末复习 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1016.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 11:38:28 | ||
图片预览










文档简介
(共34张PPT)
第七章 平面直角坐标系
章末复习课件
人教版 七年级下册
知识梳理
知识梳理
Part 1
知识梳理
知识点1 有序数对
有序数对的概念
注意:当a≠b时,(a,b)与( b,a)是两个不同的数据.
用含有两个数的表达方式来表示一个确定的位置, 其中两个数各自表示不同的含义. 我们把这种有顺序的两个数 a 与 b 组成的数对, 叫做有序数对, 记作(a, b ).
知识梳理
①“行列”定位法;
利用有序数对确定物体位置的方法:
② 经纬定位法;
③ 方格纸定位法.
对点训练
1.用7和8组成一个有序数对,可以写成( )
A.(7,8) B.(8,7)
C.7,8或8,7 D.(7,8)或(8,7)
D
2.若(1,2)表示教室里第1列第2排的位置,则教室里第2列第3排的位置表示为( )
A.(2,1) B.(3,3)
C.(2,3) D.(3,2)
C
对点训练
3.小李、小王、小张、小谢原有位置如图(横为排、竖为列),小李在第2排第4列,小王在第3排第3列,小张在第4排第2列,小谢在第5排第4列.撤走第一排,仍按照原有确定位置的方法确定新的位置,下列说法正确的是( )
A.小李现在位置为第1排第2列
B.小张现在位置为第3排第2列
C.小王现在位置为第2排第2列
D.小谢现在位置为第4排第2列
B
知识梳理
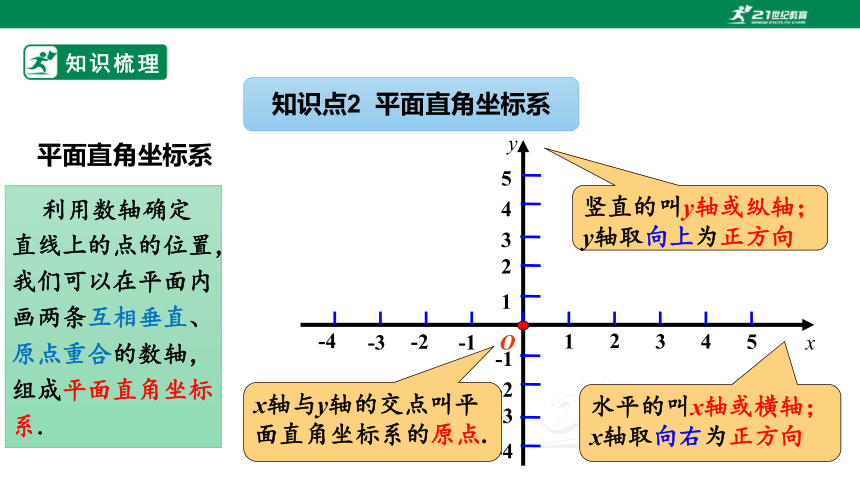
知识点2 平面直角坐标系
3
1
4
2
5
-2
-4
-1
-3
O
y
1
2
3
4
5
-4
-3
-2
-1
x
竖直的叫y轴或纵轴;
y轴取向上为正方向
水平的叫x轴或横轴;
x轴取向右为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
平面直角坐标系
利用数轴确定直线上的点的位置,我们可以在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.
知识梳理
在平面直角坐标系中:
①原点 O 的坐标为( , );
0
0
②x 轴上的点的 坐标为 ;
③y 轴上的点的 坐标为 .
0
纵
横
0
知识梳理
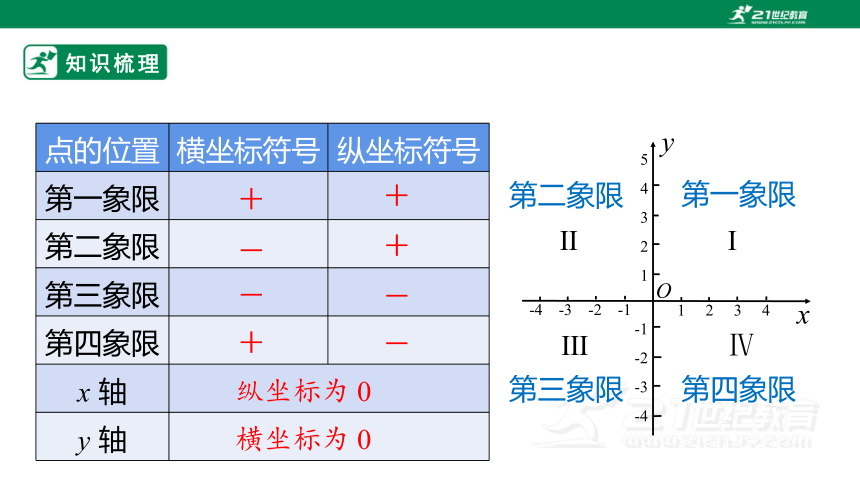
点的位置 横坐标符号 纵坐标符号
第一象限
第二象限
第三象限
第四象限
x 轴 y 轴 +
+
-
+
-
-
+
-
纵坐标为 0
横坐标为 0
Ⅳ
Ⅰ
Ⅱ
Ⅲ
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
第一象限
第二象限
第四象限
第三象限
对点训练
1.在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(a,b)所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
2.已知A(-5,0),B(3,0),点C在y轴上,△ABC的面积为12,则点C的坐标为_____________________.
(0,3)或(0,-3)
对点训练
3.已知点M到x轴的距离为3,到y轴的距离为4.
(1)若点M位于第一象限,则其坐标为________;
(2)若点M位于x轴的上方,则其坐标为_________________;
(3)若点M位于y轴的右侧,则其坐标为_________________.
(4,3)
(4,3)或(-4,3)
(4,3)或(4,-3)
知识梳理
知识点3 平面直角坐标系的应用
1.利用平面直角坐标系表示地理位置的步骤:
(1)建立平面直角坐标系,选择一个适当的参照点为原点,确定 x 轴、y 轴及其正方向;
(2)根据具体问题确定单位长度;
(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.
知识梳理
利用“方位角+距离”描述地理位置时应注意:
(1)用方位角和距离表示平面内点的位置时,必须要有两个数据:
(2)方位角的表示方法具有规定性,以正北或正南方向为基准,以向东或向西偏离的角度表示方位角,共有四种形式:
①该点相对于参照点的方位;
北偏东 x°
北偏西 x°
南偏东 x°
南偏西 x°
②该点与参照点之间的实际距离;
知识梳理
2.用坐标表示平移:
向上平移b个单位对应点P3(x,y+b)
向左平移a个单位对应点P2(x-a,y)
图形上的点P(x,y)
向下平移b个单位对应点P4(x,y-b)
向右平移a个单位对应点 P1(x+a,y)
点的平移规律
知识梳理
图形在坐标平面中的平移:
指在坐标系中,在保持坐标轴不动的情况下,图形的整体移动.
在平面直角坐标系中,对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;
反过来,从图形上的点的坐标变化,也可以得出这个图形进行了怎样的平移.
知识梳理
(1)原图形向左(右)平移a个单位长度:(a>0)
向右平移a个单位
(2)原图形向上(下)平移b个单位长度:(b>0)
原图形上的点P(x,y)
向左平移a个单位
原图形上的点P (x,y)
P1(x+a,y)
P2(x-a,y)
向上平移b个单位
原图形上的点P(x,y)
向下平移b个单位
原图形上的点P(x,y)
P3(x,y+b)
P4(x,y-b)
对点训练
1.如图是某市几个旅游景点的大致位置示意图,如果用(0,0)表示新宁莨山的位置,用(1,5)表示隆回花瑶的位置,那么城市南山的位置可以表示为( )
A.(2,1) B.(0,1)
C.(-2,-1) D.(-2,1)
C
对点训练
2.在平面直角坐标系xOy中,线段AB的两个端点坐标分别为A(-1,-1),B(1,2),平移线段AB,得到线段A′B′,已知点A′的坐标为(3,-1),则点B′的坐标为( )
A.(4,2) B.(5,2)
C.(6,2) D.(5,3)
B
对点训练
3. 将三角形ABC的三个顶点的横坐标都减1,纵坐标不变,则所得图形与原图形的位置关系是( )
A. 将原图形向x轴的正方向平移了1个单位长度
B. 将原图形向x轴的负方向平移了1个单位长度
C. 将原图形向y轴的正方向平移了1个单位长度
D. 将原图形向y轴的负方向平移了1个单位长度
B
对点训练
4.如图,请写出平行四边形ABCD各顶点的坐标,将此图形先向上平移2个单位长度,再向左平移1个单位长度得到对应图形EFGH,写出EFGH各顶点的坐标,这个四边形是平行四边形吗?
解:A(-2,1), B(1,1), C(3,-1),
D(0,-1);E(-3,3), F(0,3),
G(2,1), H(-1,1),
这个四边形是平行四边形.
对点训练
(1)图中距小明家距离相同的是哪些地方?
(2)商场B、学校A、公园C、停车场P分别在小明家的什么方向?
解:(1)图中距小明家距离相同的是学校与公园;
5.如图是小明家O和学校A所在地的简单地图.已知OA=2 cm,OB=2.5 cm,OP=4 cm,C为OP的中点.
(2)商场B在小明家的北偏西30°方向;
学校A在小明家的东北方向;
公园C、停车场P在小明家的南偏东60°方向;
对点训练
(3)如果学校距离小明家400 m,那么商场和停车场分别距离小明家多少米?
解:学校距离小明家400 m,而OA=2 cm,
故比例尺为1∶20 000.
故商场距离小明家2.5×20 000÷100=500(m);
停车场距离小明家4×20 000÷100=800(m).
提升训练
提升训练
Part 2
提升训练
1.点M在x轴的上方、y轴的左侧,且点M到x轴、y轴的距离分别为3和5,则点M的坐标为( )
A. (-5,3) B. (5,-3)
C. (-3,5) D. (3,-5)
2.在平面直角坐标系中,点P(a,a-3)的位置一定不在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
A
B
提升训练
3.若点P(x,y)在第二象限,且|x|=2,|y|=3,则x+y=( )
A. -1 B. 1 C. 5 D. -5
4. 下列说法正确的是( )
A. 若ab=0,则点P(a,b)表示原点
B. 点(-1,-a)在第三象限
C. 已知点A(3,-3)与点B(3,3),则直线AB∥x轴
D. 若ab>0,则点P(a,b)在第一、三象限
B
D
提升训练
5.以水平数轴的原点O为圆心,过正半轴Ox上的每一刻度点画同心圆,将Ox逆时针依次旋转30°,60°,90°,…,330°得到11条射线,构成如图所示的“圆”坐标系,点A,B的坐标分别表示为(5,0°),(4,300°),则点C的坐标表示为___________.
(3,240°)
提升训练
6.如图,在平面直角坐标系中,A(-1,1),B(-1,-2),C(3,-2),D(3,1),一只瓢虫从点A出发以2个单位长度/秒的速度沿A→B→C→D→A循环爬行,则第2 021秒瓢虫在( )处.
A.(3,1) B.(-1,-2)
C.(1,-2) D.(3,-2)
A
提升训练
7.已知点P(a,b)在第二象限,且|a|=3,|b|=8,求点P的坐标.
解:由第二象限内的点的横坐标小于零,得a=-3.
由第二象限内的点的纵坐标大于零,得b=8.
故点P的坐标是(-3,8).
提升训练
8. 已知点P(a-2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点Q的坐标为(1,5),直线PQ∥y轴.
解:(1)∵点P(a-2,2a+8)在x轴上,
∴2a+8=0,解得a=-4.
∴a-2=-4-2=-6.
∴点P的坐标是(-6,0).
提升训练
(2)∵点P(a-2,2a+8)在y轴上,
∴a-2=0,解得a=2.
∴2a+8=2×2+8=12.
∴点P的坐标是(0,12).
(3)∵点Q的坐标为(1,5),直线PQ∥y轴,
∴a-2=1,解得a=3.
∴2a+8=14.
∴点P的坐标是(1,14).
提升训练
9.在如图所示的平面直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(-4,10),B(-12,8),C(-14,0).求四边形OABC的面积.
提升训练
解:如图,过点A作AD⊥x轴,垂足为点D,过点B作BE⊥AD,垂足为点E.
观察上图可知D(-4,0),E(-4,8),所以BE=-4-(-12)=8,AE=10-8=2,CD=-4-(-14)=10.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第七章 平面直角坐标系
章末复习课件
人教版 七年级下册
知识梳理
知识梳理
Part 1
知识梳理
知识点1 有序数对
有序数对的概念
注意:当a≠b时,(a,b)与( b,a)是两个不同的数据.
用含有两个数的表达方式来表示一个确定的位置, 其中两个数各自表示不同的含义. 我们把这种有顺序的两个数 a 与 b 组成的数对, 叫做有序数对, 记作(a, b ).
知识梳理
①“行列”定位法;
利用有序数对确定物体位置的方法:
② 经纬定位法;
③ 方格纸定位法.
对点训练
1.用7和8组成一个有序数对,可以写成( )
A.(7,8) B.(8,7)
C.7,8或8,7 D.(7,8)或(8,7)
D
2.若(1,2)表示教室里第1列第2排的位置,则教室里第2列第3排的位置表示为( )
A.(2,1) B.(3,3)
C.(2,3) D.(3,2)
C
对点训练
3.小李、小王、小张、小谢原有位置如图(横为排、竖为列),小李在第2排第4列,小王在第3排第3列,小张在第4排第2列,小谢在第5排第4列.撤走第一排,仍按照原有确定位置的方法确定新的位置,下列说法正确的是( )
A.小李现在位置为第1排第2列
B.小张现在位置为第3排第2列
C.小王现在位置为第2排第2列
D.小谢现在位置为第4排第2列
B
知识梳理
知识点2 平面直角坐标系
3
1
4
2
5
-2
-4
-1
-3
O
y
1
2
3
4
5
-4
-3
-2
-1
x
竖直的叫y轴或纵轴;
y轴取向上为正方向
水平的叫x轴或横轴;
x轴取向右为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
平面直角坐标系
利用数轴确定直线上的点的位置,我们可以在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.
知识梳理
在平面直角坐标系中:
①原点 O 的坐标为( , );
0
0
②x 轴上的点的 坐标为 ;
③y 轴上的点的 坐标为 .
0
纵
横
0
知识梳理
点的位置 横坐标符号 纵坐标符号
第一象限
第二象限
第三象限
第四象限
x 轴 y 轴 +
+
-
+
-
-
+
-
纵坐标为 0
横坐标为 0
Ⅳ
Ⅰ
Ⅱ
Ⅲ
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
第一象限
第二象限
第四象限
第三象限
对点训练
1.在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(a,b)所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
2.已知A(-5,0),B(3,0),点C在y轴上,△ABC的面积为12,则点C的坐标为_____________________.
(0,3)或(0,-3)
对点训练
3.已知点M到x轴的距离为3,到y轴的距离为4.
(1)若点M位于第一象限,则其坐标为________;
(2)若点M位于x轴的上方,则其坐标为_________________;
(3)若点M位于y轴的右侧,则其坐标为_________________.
(4,3)
(4,3)或(-4,3)
(4,3)或(4,-3)
知识梳理
知识点3 平面直角坐标系的应用
1.利用平面直角坐标系表示地理位置的步骤:
(1)建立平面直角坐标系,选择一个适当的参照点为原点,确定 x 轴、y 轴及其正方向;
(2)根据具体问题确定单位长度;
(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.
知识梳理
利用“方位角+距离”描述地理位置时应注意:
(1)用方位角和距离表示平面内点的位置时,必须要有两个数据:
(2)方位角的表示方法具有规定性,以正北或正南方向为基准,以向东或向西偏离的角度表示方位角,共有四种形式:
①该点相对于参照点的方位;
北偏东 x°
北偏西 x°
南偏东 x°
南偏西 x°
②该点与参照点之间的实际距离;
知识梳理
2.用坐标表示平移:
向上平移b个单位对应点P3(x,y+b)
向左平移a个单位对应点P2(x-a,y)
图形上的点P(x,y)
向下平移b个单位对应点P4(x,y-b)
向右平移a个单位对应点 P1(x+a,y)
点的平移规律
知识梳理
图形在坐标平面中的平移:
指在坐标系中,在保持坐标轴不动的情况下,图形的整体移动.
在平面直角坐标系中,对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;
反过来,从图形上的点的坐标变化,也可以得出这个图形进行了怎样的平移.
知识梳理
(1)原图形向左(右)平移a个单位长度:(a>0)
向右平移a个单位
(2)原图形向上(下)平移b个单位长度:(b>0)
原图形上的点P(x,y)
向左平移a个单位
原图形上的点P (x,y)
P1(x+a,y)
P2(x-a,y)
向上平移b个单位
原图形上的点P(x,y)
向下平移b个单位
原图形上的点P(x,y)
P3(x,y+b)
P4(x,y-b)
对点训练
1.如图是某市几个旅游景点的大致位置示意图,如果用(0,0)表示新宁莨山的位置,用(1,5)表示隆回花瑶的位置,那么城市南山的位置可以表示为( )
A.(2,1) B.(0,1)
C.(-2,-1) D.(-2,1)
C
对点训练
2.在平面直角坐标系xOy中,线段AB的两个端点坐标分别为A(-1,-1),B(1,2),平移线段AB,得到线段A′B′,已知点A′的坐标为(3,-1),则点B′的坐标为( )
A.(4,2) B.(5,2)
C.(6,2) D.(5,3)
B
对点训练
3. 将三角形ABC的三个顶点的横坐标都减1,纵坐标不变,则所得图形与原图形的位置关系是( )
A. 将原图形向x轴的正方向平移了1个单位长度
B. 将原图形向x轴的负方向平移了1个单位长度
C. 将原图形向y轴的正方向平移了1个单位长度
D. 将原图形向y轴的负方向平移了1个单位长度
B
对点训练
4.如图,请写出平行四边形ABCD各顶点的坐标,将此图形先向上平移2个单位长度,再向左平移1个单位长度得到对应图形EFGH,写出EFGH各顶点的坐标,这个四边形是平行四边形吗?
解:A(-2,1), B(1,1), C(3,-1),
D(0,-1);E(-3,3), F(0,3),
G(2,1), H(-1,1),
这个四边形是平行四边形.
对点训练
(1)图中距小明家距离相同的是哪些地方?
(2)商场B、学校A、公园C、停车场P分别在小明家的什么方向?
解:(1)图中距小明家距离相同的是学校与公园;
5.如图是小明家O和学校A所在地的简单地图.已知OA=2 cm,OB=2.5 cm,OP=4 cm,C为OP的中点.
(2)商场B在小明家的北偏西30°方向;
学校A在小明家的东北方向;
公园C、停车场P在小明家的南偏东60°方向;
对点训练
(3)如果学校距离小明家400 m,那么商场和停车场分别距离小明家多少米?
解:学校距离小明家400 m,而OA=2 cm,
故比例尺为1∶20 000.
故商场距离小明家2.5×20 000÷100=500(m);
停车场距离小明家4×20 000÷100=800(m).
提升训练
提升训练
Part 2
提升训练
1.点M在x轴的上方、y轴的左侧,且点M到x轴、y轴的距离分别为3和5,则点M的坐标为( )
A. (-5,3) B. (5,-3)
C. (-3,5) D. (3,-5)
2.在平面直角坐标系中,点P(a,a-3)的位置一定不在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
A
B
提升训练
3.若点P(x,y)在第二象限,且|x|=2,|y|=3,则x+y=( )
A. -1 B. 1 C. 5 D. -5
4. 下列说法正确的是( )
A. 若ab=0,则点P(a,b)表示原点
B. 点(-1,-a)在第三象限
C. 已知点A(3,-3)与点B(3,3),则直线AB∥x轴
D. 若ab>0,则点P(a,b)在第一、三象限
B
D
提升训练
5.以水平数轴的原点O为圆心,过正半轴Ox上的每一刻度点画同心圆,将Ox逆时针依次旋转30°,60°,90°,…,330°得到11条射线,构成如图所示的“圆”坐标系,点A,B的坐标分别表示为(5,0°),(4,300°),则点C的坐标表示为___________.
(3,240°)
提升训练
6.如图,在平面直角坐标系中,A(-1,1),B(-1,-2),C(3,-2),D(3,1),一只瓢虫从点A出发以2个单位长度/秒的速度沿A→B→C→D→A循环爬行,则第2 021秒瓢虫在( )处.
A.(3,1) B.(-1,-2)
C.(1,-2) D.(3,-2)
A
提升训练
7.已知点P(a,b)在第二象限,且|a|=3,|b|=8,求点P的坐标.
解:由第二象限内的点的横坐标小于零,得a=-3.
由第二象限内的点的纵坐标大于零,得b=8.
故点P的坐标是(-3,8).
提升训练
8. 已知点P(a-2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点Q的坐标为(1,5),直线PQ∥y轴.
解:(1)∵点P(a-2,2a+8)在x轴上,
∴2a+8=0,解得a=-4.
∴a-2=-4-2=-6.
∴点P的坐标是(-6,0).
提升训练
(2)∵点P(a-2,2a+8)在y轴上,
∴a-2=0,解得a=2.
∴2a+8=2×2+8=12.
∴点P的坐标是(0,12).
(3)∵点Q的坐标为(1,5),直线PQ∥y轴,
∴a-2=1,解得a=3.
∴2a+8=14.
∴点P的坐标是(1,14).
提升训练
9.在如图所示的平面直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(-4,10),B(-12,8),C(-14,0).求四边形OABC的面积.
提升训练
解:如图,过点A作AD⊥x轴,垂足为点D,过点B作BE⊥AD,垂足为点E.
观察上图可知D(-4,0),E(-4,8),所以BE=-4-(-12)=8,AE=10-8=2,CD=-4-(-14)=10.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
