人教版数学八年级下册 第18章 平行四边形的折叠问题专题复习 课件(共16张PPT)
文档属性
| 名称 | 人教版数学八年级下册 第18章 平行四边形的折叠问题专题复习 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 371.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-04 20:36:08 | ||
图片预览


文档简介
(共16张PPT)
平行四边形的折叠问题
解决平行四边形的折叠问题,既要用到轴对称的性质,有时还需要借助勾股定理进行相关运算。接下来,我们通过几个例题来探究平行四边形中的折叠问题。
【导入新课】
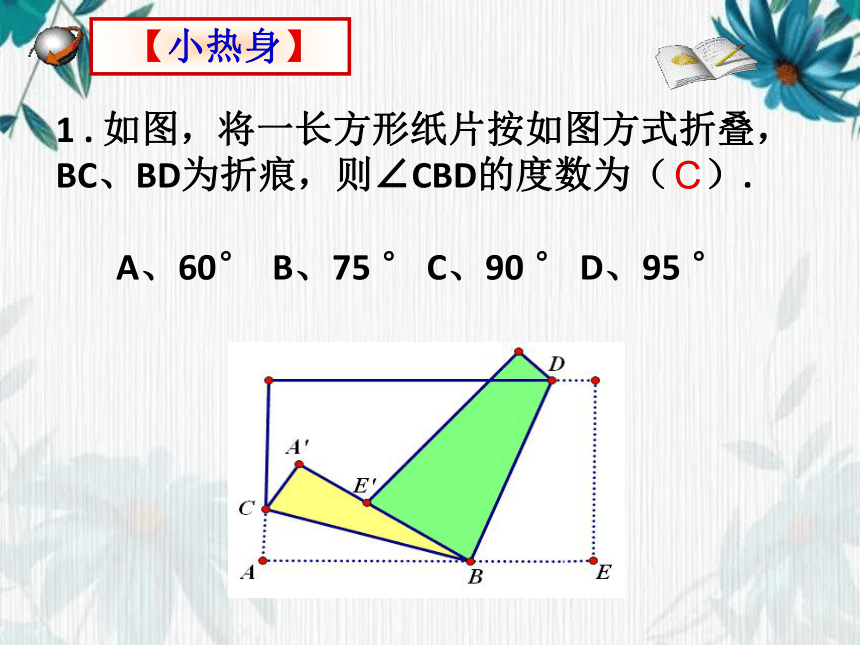
1 . 如图,将一长方形纸片按如图方式折叠, BC、BD为折痕,则∠CBD的度数为( ).
A、60° B、75 ° C、90 ° D、95 °
【小热身】
C
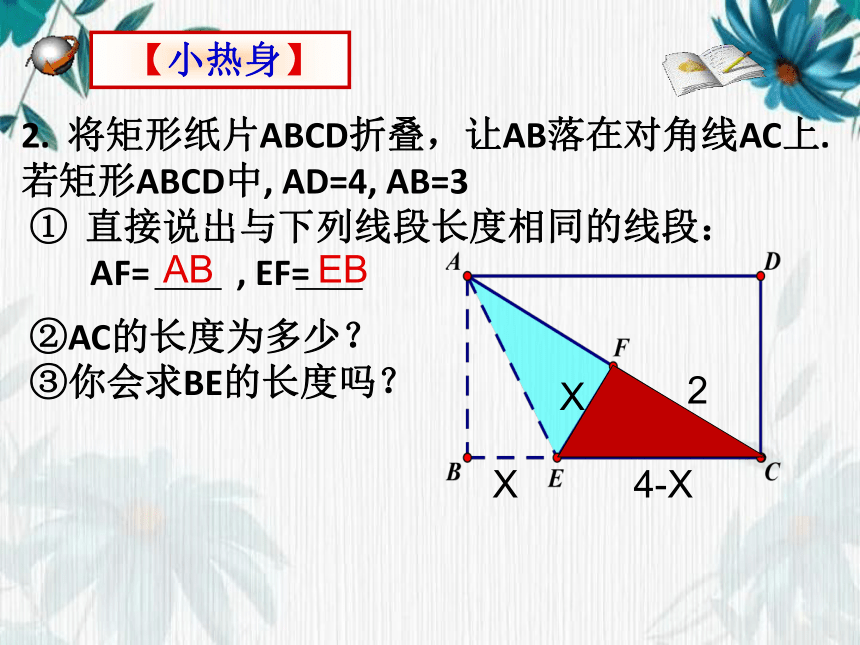
2. 将矩形纸片ABCD折叠,让AB落在对角线AC上.
若矩形ABCD中, AD=4, AB=3
① 直接说出与下列线段长度相同的线段:
AF= , EF=
【小热身】
②AC的长度为多少?
③你会求BE的长度吗?
AB
EB
2
X
X
4-X
【合作探究一】
A
B
C
D
E
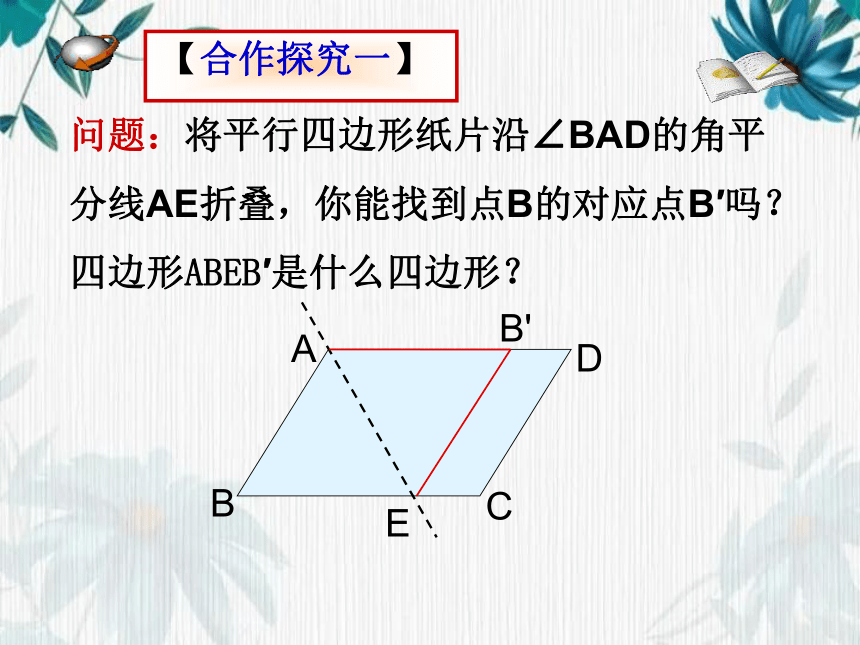
问题:将平行四边形纸片沿∠BAD的角平
分线AE折叠,你能找到点B的对应点B′吗?
四边形ABEB′是什么四边形?
B'
【合作探究一】
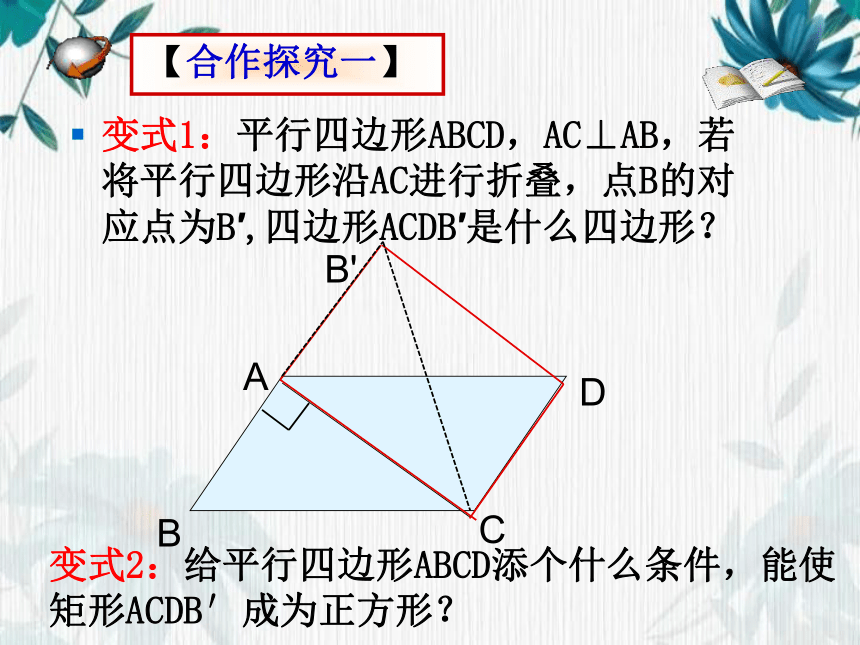
变式1:平行四边形ABCD,AC⊥AB,若将平行四边形沿AC进行折叠,点B的对应点为B′,四边形ACDB′是什么四边形?
B
A
C
D
变式2:给平行四边形ABCD添个什么条件,能使矩形ACDB′成为正方形?
B'
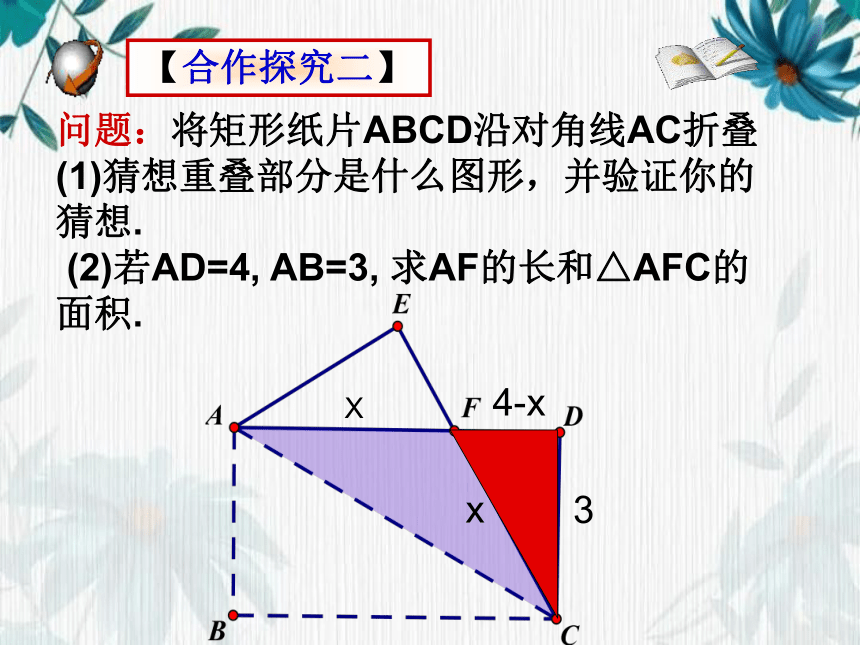
问题:将矩形纸片ABCD沿对角线AC折叠
(1)猜想重叠部分是什么图形,并验证你的猜想.
(2)若AD=4, AB=3, 求AF的长和△AFC的面积.
【合作探究二】
x
3
4-x
X
【实践运用】
问题:将一张平行四边形纸片折一次,使折痕平分这个平行四边形的面积,这样的折叠方法有几种?
这些折痕有什么共性?
O
A
B
C
D
E
F
如图,折叠长方形的一边AD,点D落在BC边的点F处,已知AB=8cm,AD=10cm,求EC的长.
8
10
6
4
【巩固练习一】
A
B
C
D
F
E
x
8-x
【巩固练习二】
将矩形ABCD折叠使A、C重合,折痕交BC于E,交AD于F,交AC于O.
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,
求菱形AECF的边长;
求折痕EF的长.
A
B
C
D
F
E
O
4
x
8-x
x
G
提出问题
问题1:解决折叠问题主要运用了哪些知识点
问题2:在用勾股定理解决折叠中的运算问题时,怎样寻求解题思路?
1、如图,在直角坐标系中放入一边长OC为6的
矩形纸片ABCO,将纸翻折后,使点B恰好落在x轴上,记为B′,折痕为CE,已知OC:OB′=3:4
(1)求出B′点的坐标;
(2)求折痕CE所在直线
的解析式。
【拓展练习一】
【拓展练习二】
A
B
D
C
2.在三角形ABC中,∠BAC=45°,AD⊥BC,BD=2,CD=1,求AD的长.
小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题。请按照小萍的思路,探究并解答这个问题。
F
G
E
小萍的思路:分别以AB、AC为折痕,画出 ABD 和 ACD折叠后的图形,点D的对应点分别落在点F,点E处,延长FB、EC相交于点G.证明四边形AFGE是正方形。
1.已知,如图长方形ABCD中,AB=3cm,AD=9cm,
将此长方形折叠,使点B与点D重合,折痕为EF,
(1)BE与BF相等吗?
(2)求BE的长.
(3)求 BEF的面积.
A
E
D
B (D')
C'
C
F
家庭作业
折叠问题
1、本质:轴对称(全等性,对称性)
2、关键:
翻折
全等
相等的边
相等的角
【课堂小结】
3、方法:构建直角三角形,利用 勾股定理建立方程
再见!
平行四边形的折叠问题
解决平行四边形的折叠问题,既要用到轴对称的性质,有时还需要借助勾股定理进行相关运算。接下来,我们通过几个例题来探究平行四边形中的折叠问题。
【导入新课】
1 . 如图,将一长方形纸片按如图方式折叠, BC、BD为折痕,则∠CBD的度数为( ).
A、60° B、75 ° C、90 ° D、95 °
【小热身】
C
2. 将矩形纸片ABCD折叠,让AB落在对角线AC上.
若矩形ABCD中, AD=4, AB=3
① 直接说出与下列线段长度相同的线段:
AF= , EF=
【小热身】
②AC的长度为多少?
③你会求BE的长度吗?
AB
EB
2
X
X
4-X
【合作探究一】
A
B
C
D
E
问题:将平行四边形纸片沿∠BAD的角平
分线AE折叠,你能找到点B的对应点B′吗?
四边形ABEB′是什么四边形?
B'
【合作探究一】
变式1:平行四边形ABCD,AC⊥AB,若将平行四边形沿AC进行折叠,点B的对应点为B′,四边形ACDB′是什么四边形?
B
A
C
D
变式2:给平行四边形ABCD添个什么条件,能使矩形ACDB′成为正方形?
B'
问题:将矩形纸片ABCD沿对角线AC折叠
(1)猜想重叠部分是什么图形,并验证你的猜想.
(2)若AD=4, AB=3, 求AF的长和△AFC的面积.
【合作探究二】
x
3
4-x
X
【实践运用】
问题:将一张平行四边形纸片折一次,使折痕平分这个平行四边形的面积,这样的折叠方法有几种?
这些折痕有什么共性?
O
A
B
C
D
E
F
如图,折叠长方形的一边AD,点D落在BC边的点F处,已知AB=8cm,AD=10cm,求EC的长.
8
10
6
4
【巩固练习一】
A
B
C
D
F
E
x
8-x
【巩固练习二】
将矩形ABCD折叠使A、C重合,折痕交BC于E,交AD于F,交AC于O.
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,
求菱形AECF的边长;
求折痕EF的长.
A
B
C
D
F
E
O
4
x
8-x
x
G
提出问题
问题1:解决折叠问题主要运用了哪些知识点
问题2:在用勾股定理解决折叠中的运算问题时,怎样寻求解题思路?
1、如图,在直角坐标系中放入一边长OC为6的
矩形纸片ABCO,将纸翻折后,使点B恰好落在x轴上,记为B′,折痕为CE,已知OC:OB′=3:4
(1)求出B′点的坐标;
(2)求折痕CE所在直线
的解析式。
【拓展练习一】
【拓展练习二】
A
B
D
C
2.在三角形ABC中,∠BAC=45°,AD⊥BC,BD=2,CD=1,求AD的长.
小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题。请按照小萍的思路,探究并解答这个问题。
F
G
E
小萍的思路:分别以AB、AC为折痕,画出 ABD 和 ACD折叠后的图形,点D的对应点分别落在点F,点E处,延长FB、EC相交于点G.证明四边形AFGE是正方形。
1.已知,如图长方形ABCD中,AB=3cm,AD=9cm,
将此长方形折叠,使点B与点D重合,折痕为EF,
(1)BE与BF相等吗?
(2)求BE的长.
(3)求 BEF的面积.
A
E
D
B (D')
C'
C
F
家庭作业
折叠问题
1、本质:轴对称(全等性,对称性)
2、关键:
翻折
全等
相等的边
相等的角
【课堂小结】
3、方法:构建直角三角形,利用 勾股定理建立方程
再见!
