苏科版 八年级下册 第11章 反比例函数复习课 优质课件(共18张PPT)
文档属性
| 名称 | 苏科版 八年级下册 第11章 反比例函数复习课 优质课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1003.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 08:53:37 | ||
图片预览





文档简介
(共18张PPT)
《反比例函数》
1.什么叫反比例函数?
形如 的函数称为反比例函数。
(k为常数,k≠0)
2.反比例函数等价形式
y=kx-1
xy=k
一、概念:
(k为常数,k≠0)
1.若 为反比例函数,则m=______ .
2.若 为反比例函数,则
m=______ .
2
-1
做一做:
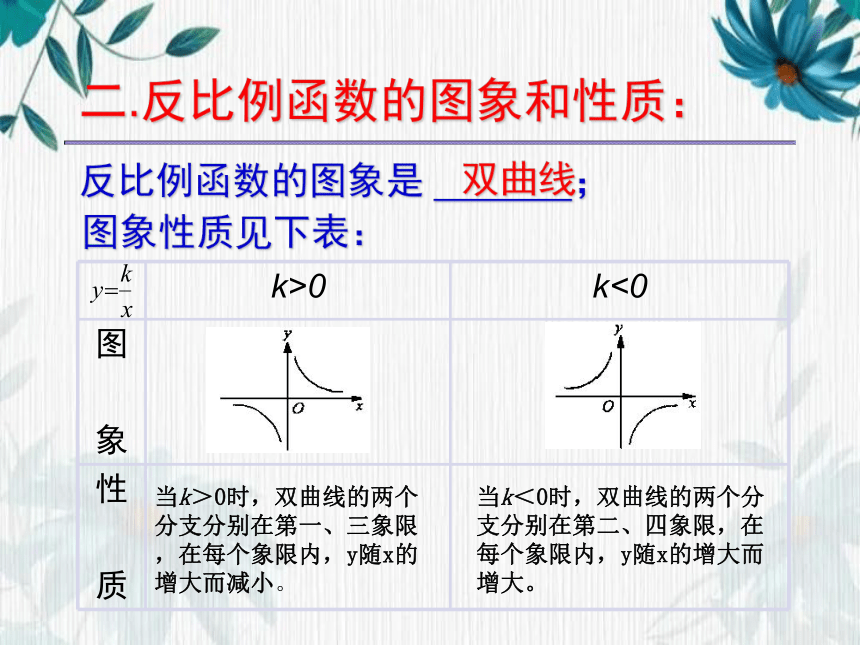
二.反比例函数的图象和性质:
反比例函数的图象是 ;
双曲线
图象性质见下表:
k>0 k<0
图
象
性
质
当k>0时,双曲线的两个分支分别在第一、三象限,在每个象限内,y随x的增大而减小。
当k<0时,双曲线的两个分支分别在第二、四象限,在每个象限内,y随x的增大而增大。
做一做:
1.函数 的图象在第______象限,当x<0时,
y随x的增大而______ .
2.双曲线 经过点 (-3 ,______ ).
3.函数 的图象在二、四象限内,m的取值
范围是______ .
4.若双曲线经过点(-3 ,2),则其解析式是______.
一、三
减小
1
9
m<2
6
x
y
=
5、在反比例函数 的图象上有两点
(x1,y1)、(x2,y2), 若x1>x2 >0,则y1与y2
的大小关系是 。
变:
1)若x1 >0 >x2,则y1与y2 的大小关系是 。
2)若x1>x2,则y1与y2 的大小关系是 。
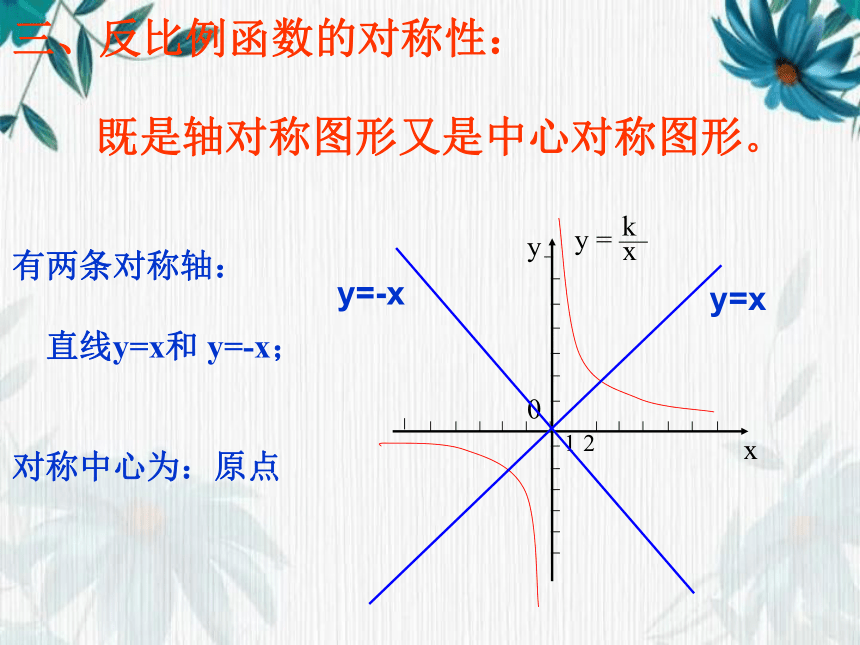
三、反比例函数的对称性:
既是轴对称图形又是中心对称图形。
x
y
0
1
2
y = —
k
x
y=x
y=-x
有两条对称轴:
直线y=x和 y=-x;
对称中心为:原点
1、如图,过原点的一条直线与反比例函数
(k≠0)的图象分别交于A、B两点,若点A的坐标(a,b),
则点B的坐标为( )
A. (b,a) B. (-a,b)
C. (-b,-a) D. (-a,-b)
y
0
x
B
A
P(x,y)
A
o
y
x
B
四、k的几何意义:
B
1、已知点A是反比例函数 上的点,
过点A作 AP⊥ x轴于点p,则△AOP的面积为
( )
A. 12 B. 6
C. 4 D. 3
x
y
0
P
A
2、如图:A、C是函数 的图象上任意两点,
A.S1>S2
B.S1C.S1 = S2
D.S1和S2的大小关系不能确定.
C
A
B
o
y
x
C
D
D
S1
S2
A
C
o
y
x
P
____
,
3
,
,
,
,
3、
函数的解析式是
则这个反比例
阴影部分面积为
轴引垂线
轴
向
分别
由
图像上的一点
是反比例函数
如图
y
x
P
x
k
y
P
=
.
3
x
y
-
=
4、若点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,垂足分别为点M、N,若四边形PMON面积为3,则这个反比例函数的关系式是
________________________.
提示:S矩形=|xy|= |k| 则 k=s或-s
或
5、如下图是三个反比例函数
,
在x轴上方的图象,由此观察得到的k1,k2,k3大小关系为( )
B
例题1:右图描述的是一辆小轿车在一条高速公路上匀速前进的图象,根据图象提供的信息回答下列问题:
(1)这条高速公路全长是多少千米?
(2)写出时间t与速度v之间的函数关系式;
(3)如果2至3h到达,轿车速度在什么范围?
v(km/h)
150
2
O
100
200
t(h)
300千米
100至150(千米/小时)
3
由图象得
当2 ≤ t ≤3时, 100≤v≤150
(1)
(2)
(3)
解:
五、实际问题与反比例函数
例题2:如图,某学校对教室采用药熏消毒法进行消毒。
已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例.
现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg。请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,求y与x的关系式;
(2)药物燃烧完后,求y与x的关系式;
(3)研究表明,当空气中每立方米的含药量低于1.6 mg时学生方可进入教室,那么从消毒开始,至少经过多少min后,学生才能回到教室;
1.函数 与 在同一条直
角坐标系中的图象可能是_______:
六、一次函数与反比例函数:
x
y
o
x
y
o
x
y
o
x
y
o
A. B. C. D.
2、如图,一次函数y1 =kx+b的图象与反比例函数
的图象交于 A(-2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)若y1﹥y时,求x 的取值范围;
(3)求⊿AOB的面积.
O
y
x
B
A
C
D
《反比例函数》
1.什么叫反比例函数?
形如 的函数称为反比例函数。
(k为常数,k≠0)
2.反比例函数等价形式
y=kx-1
xy=k
一、概念:
(k为常数,k≠0)
1.若 为反比例函数,则m=______ .
2.若 为反比例函数,则
m=______ .
2
-1
做一做:
二.反比例函数的图象和性质:
反比例函数的图象是 ;
双曲线
图象性质见下表:
k>0 k<0
图
象
性
质
当k>0时,双曲线的两个分支分别在第一、三象限,在每个象限内,y随x的增大而减小。
当k<0时,双曲线的两个分支分别在第二、四象限,在每个象限内,y随x的增大而增大。
做一做:
1.函数 的图象在第______象限,当x<0时,
y随x的增大而______ .
2.双曲线 经过点 (-3 ,______ ).
3.函数 的图象在二、四象限内,m的取值
范围是______ .
4.若双曲线经过点(-3 ,2),则其解析式是______.
一、三
减小
1
9
m<2
6
x
y
=
5、在反比例函数 的图象上有两点
(x1,y1)、(x2,y2), 若x1>x2 >0,则y1与y2
的大小关系是 。
变:
1)若x1 >0 >x2,则y1与y2 的大小关系是 。
2)若x1>x2,则y1与y2 的大小关系是 。
三、反比例函数的对称性:
既是轴对称图形又是中心对称图形。
x
y
0
1
2
y = —
k
x
y=x
y=-x
有两条对称轴:
直线y=x和 y=-x;
对称中心为:原点
1、如图,过原点的一条直线与反比例函数
(k≠0)的图象分别交于A、B两点,若点A的坐标(a,b),
则点B的坐标为( )
A. (b,a) B. (-a,b)
C. (-b,-a) D. (-a,-b)
y
0
x
B
A
P(x,y)
A
o
y
x
B
四、k的几何意义:
B
1、已知点A是反比例函数 上的点,
过点A作 AP⊥ x轴于点p,则△AOP的面积为
( )
A. 12 B. 6
C. 4 D. 3
x
y
0
P
A
2、如图:A、C是函数 的图象上任意两点,
A.S1>S2
B.S1
D.S1和S2的大小关系不能确定.
C
A
B
o
y
x
C
D
D
S1
S2
A
C
o
y
x
P
____
,
3
,
,
,
,
3、
函数的解析式是
则这个反比例
阴影部分面积为
轴引垂线
轴
向
分别
由
图像上的一点
是反比例函数
如图
y
x
P
x
k
y
P
=
.
3
x
y
-
=
4、若点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,垂足分别为点M、N,若四边形PMON面积为3,则这个反比例函数的关系式是
________________________.
提示:S矩形=|xy|= |k| 则 k=s或-s
或
5、如下图是三个反比例函数
,
在x轴上方的图象,由此观察得到的k1,k2,k3大小关系为( )
B
例题1:右图描述的是一辆小轿车在一条高速公路上匀速前进的图象,根据图象提供的信息回答下列问题:
(1)这条高速公路全长是多少千米?
(2)写出时间t与速度v之间的函数关系式;
(3)如果2至3h到达,轿车速度在什么范围?
v(km/h)
150
2
O
100
200
t(h)
300千米
100至150(千米/小时)
3
由图象得
当2 ≤ t ≤3时, 100≤v≤150
(1)
(2)
(3)
解:
五、实际问题与反比例函数
例题2:如图,某学校对教室采用药熏消毒法进行消毒。
已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例.
现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg。请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,求y与x的关系式;
(2)药物燃烧完后,求y与x的关系式;
(3)研究表明,当空气中每立方米的含药量低于1.6 mg时学生方可进入教室,那么从消毒开始,至少经过多少min后,学生才能回到教室;
1.函数 与 在同一条直
角坐标系中的图象可能是_______:
六、一次函数与反比例函数:
x
y
o
x
y
o
x
y
o
x
y
o
A. B. C. D.
2、如图,一次函数y1 =kx+b的图象与反比例函数
的图象交于 A(-2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)若y1﹥y时,求x 的取值范围;
(3)求⊿AOB的面积.
O
y
x
B
A
C
D
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
