苏科版 七年级下册 7.2 平行线中的折线成角问题 优质课件(共15张PPT)
文档属性
| 名称 | 苏科版 七年级下册 7.2 平行线中的折线成角问题 优质课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 833.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 07:02:54 | ||
图片预览




文档简介
(共15张PPT)
平行线中的折线成角
学习目标
1. 运用“平行线被折线所截”的基本图形和结论解决平行线中的折线成角问题.
2.通过观察、探究折角与边角之间的数量关系,体会图形之间的变化和联系.
重难点:基本图形和对应结论的灵活应用.
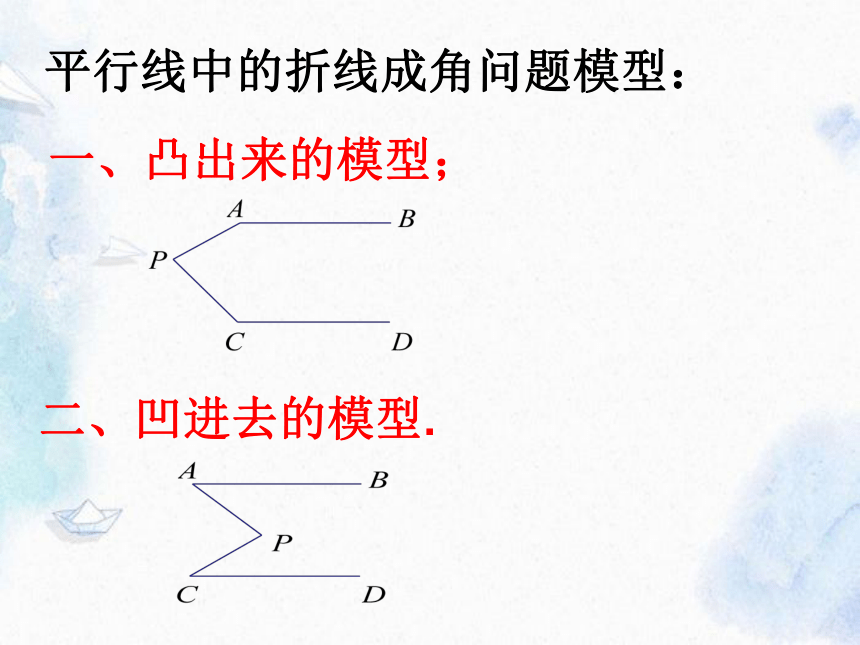
平行线中的折线成角问题模型:
一、凸出来的模型;
二、凹进去的模型.
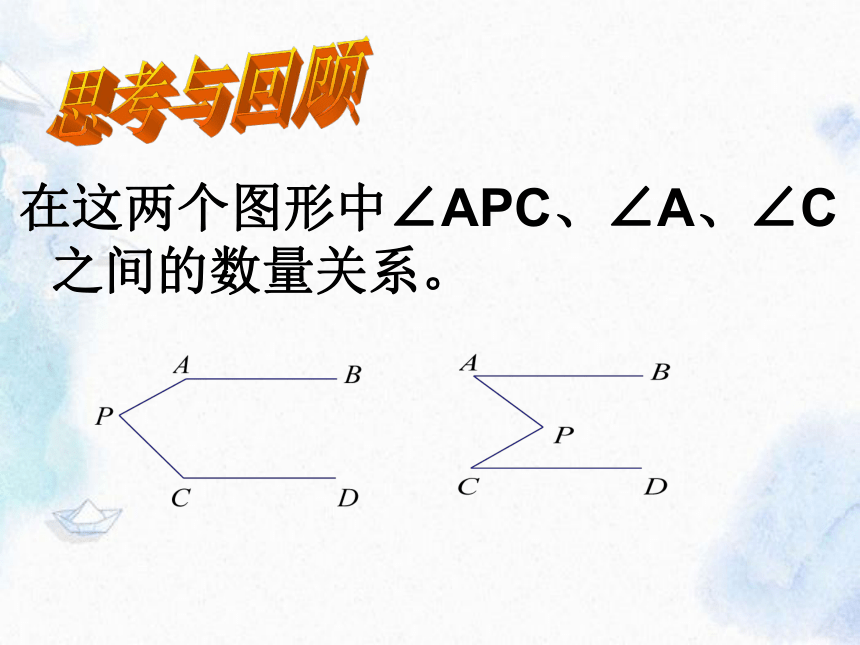
在这两个图形中∠APC、∠A、∠C之间的数量关系。
思考与回顾
基本图形一
1
2
E
两直线平行同旁内角互补
基本图形二
∠A+∠C=∠APC
两直线平行内错角相等
1
2
E
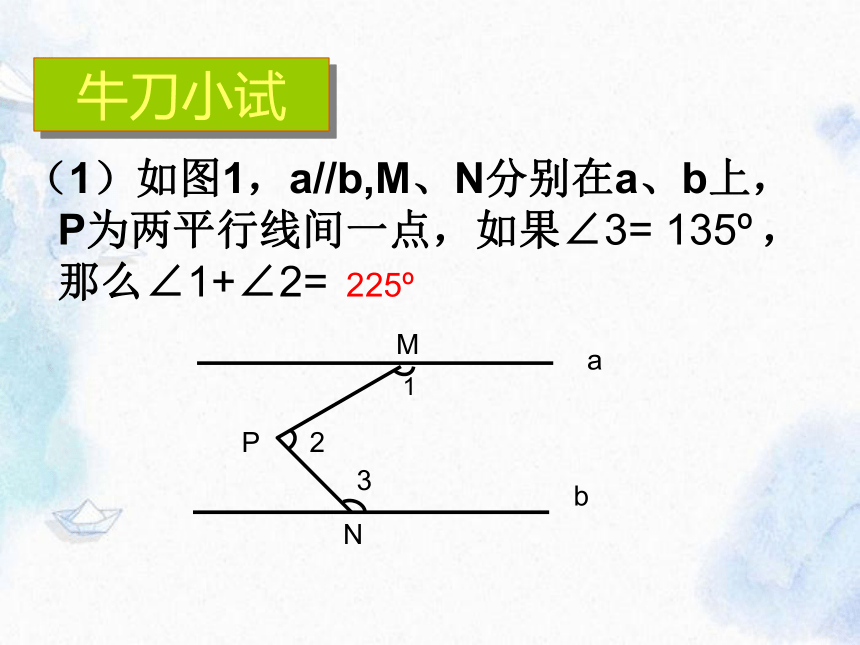
牛刀小试
(1)如图1,a//b,M、N分别在a、b上,P为两平行线间一点,如果∠3= 135 ,那么∠1+∠2=
a
b
M
P
N
2
3
225
1
(2)如图2,AB∥CD,∠A=65°- α ∠P=80°+α,∠C=60°-α,则α=
牛刀小试
A
B
P
C
D
15
当点P在平行线AB、CD的内部的时候,我们可以得到子弹图和猪手图,如果点P运动到平行线AB、CD的外部,可以得到哪些不同的图形呢?在这些图形中∠APC、与∠A、∠C之间有什么数量关系?
思考 探 究
“猪手图”变式
火眼金睛发现
当折点在平行线的外部时,折角等于两个边角之差.
(即:折角=大边角-小边角)
例1:已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E = 140 ,则∠F=
精典例题
110°
学法指导:
(1) 由基本图形二,你能得到∠F与∠1+∠3的关系吗?
(2)由基本图形一,你能得到∠ABE+∠CDE的值吗?
(3)由BF和DF分别平分∠ABE和∠CDE,你能得到∠1+∠3 与∠ABE+∠CDE的关系吗?
将上题中的∠ABE的平分线改为它的补∠ABG的角平分线,其它条件不变,则∠F=
学法指导:
(1)由基本图形四,你能得到∠F与
∠1、∠3的关系吗?
(2)由基本图形一,你能得到你能得
到∠ABE+∠CDE的值吗?
(3)由第(2)问的结论,将∠ABE转
化成∠1,将∠CDE转化成∠3,看看
你能得到什么结论?
变式题
20度
变式题:将上题中的∠ABE的平分线改为它的补角∠ABG的角平分线,其它条件不变,则∠F=
学法指导:
1)由基本图形四,你能得到∠F与∠1和∠3的
关系吗?
2)由基本图形一,你能得到你能得到
∠ABE+∠CDE的值吗?
3)由第(2)问的结论,将∠ABE转化成∠1,
将∠CDE转化成∠3,看看你能得到什么结论?
变式题
由∠F+∠1=∠3 可得 ∠F=∠3-∠1
由∠ABE+∠CDE+∠E=360 可得∠ABE+∠CDE=220
因为∠ABE=180 -2∠1 ,∠CDE=2∠3 ,所以180 -2∠1 +2∠3 =220 ,所以2∠3 -2∠1 =40 所以∠3 -∠1 =20 即 ∠F=20
20
畅所欲言
这节课你有哪些收获和感悟?
平行线中的折线成角
学习目标
1. 运用“平行线被折线所截”的基本图形和结论解决平行线中的折线成角问题.
2.通过观察、探究折角与边角之间的数量关系,体会图形之间的变化和联系.
重难点:基本图形和对应结论的灵活应用.
平行线中的折线成角问题模型:
一、凸出来的模型;
二、凹进去的模型.
在这两个图形中∠APC、∠A、∠C之间的数量关系。
思考与回顾
基本图形一
1
2
E
两直线平行同旁内角互补
基本图形二
∠A+∠C=∠APC
两直线平行内错角相等
1
2
E
牛刀小试
(1)如图1,a//b,M、N分别在a、b上,P为两平行线间一点,如果∠3= 135 ,那么∠1+∠2=
a
b
M
P
N
2
3
225
1
(2)如图2,AB∥CD,∠A=65°- α ∠P=80°+α,∠C=60°-α,则α=
牛刀小试
A
B
P
C
D
15
当点P在平行线AB、CD的内部的时候,我们可以得到子弹图和猪手图,如果点P运动到平行线AB、CD的外部,可以得到哪些不同的图形呢?在这些图形中∠APC、与∠A、∠C之间有什么数量关系?
思考 探 究
“猪手图”变式
火眼金睛发现
当折点在平行线的外部时,折角等于两个边角之差.
(即:折角=大边角-小边角)
例1:已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E = 140 ,则∠F=
精典例题
110°
学法指导:
(1) 由基本图形二,你能得到∠F与∠1+∠3的关系吗?
(2)由基本图形一,你能得到∠ABE+∠CDE的值吗?
(3)由BF和DF分别平分∠ABE和∠CDE,你能得到∠1+∠3 与∠ABE+∠CDE的关系吗?
将上题中的∠ABE的平分线改为它的补∠ABG的角平分线,其它条件不变,则∠F=
学法指导:
(1)由基本图形四,你能得到∠F与
∠1、∠3的关系吗?
(2)由基本图形一,你能得到你能得
到∠ABE+∠CDE的值吗?
(3)由第(2)问的结论,将∠ABE转
化成∠1,将∠CDE转化成∠3,看看
你能得到什么结论?
变式题
20度
变式题:将上题中的∠ABE的平分线改为它的补角∠ABG的角平分线,其它条件不变,则∠F=
学法指导:
1)由基本图形四,你能得到∠F与∠1和∠3的
关系吗?
2)由基本图形一,你能得到你能得到
∠ABE+∠CDE的值吗?
3)由第(2)问的结论,将∠ABE转化成∠1,
将∠CDE转化成∠3,看看你能得到什么结论?
变式题
由∠F+∠1=∠3 可得 ∠F=∠3-∠1
由∠ABE+∠CDE+∠E=360 可得∠ABE+∠CDE=220
因为∠ABE=180 -2∠1 ,∠CDE=2∠3 ,所以180 -2∠1 +2∠3 =220 ,所以2∠3 -2∠1 =40 所以∠3 -∠1 =20 即 ∠F=20
20
畅所欲言
这节课你有哪些收获和感悟?
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
