人教版 七年级下册 8.3 二元一次方程组与实际问题(共19张PPT)
文档属性
| 名称 | 人教版 七年级下册 8.3 二元一次方程组与实际问题(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 09:18:43 | ||
图片预览




文档简介
(共19张PPT)
新人教版初中数学七年级下册第八章
学习目标
会用列表法分析应用题中的数量关系,列出相应的二元一次方程组解决复杂的实际问题,并进一步提高解方程组的技能。
学习重点:用列表的方式分析题中的各个量的关系,列出二元一次方程组。
学习难点:从列表中获取信息,借助列表分析问题中所蕴含的数量关系。
一、问题导入
经调查,某小组6个人5天共吃了90个馒头,
问:平均每人每天吃多少个馒头?
2.把2吨货物从A地运到100千米外的B地,共支付
运费300元。问:运1吨的货物行驶1千米,需要
支付多少钱?
1人1天吃3个馒头 3个/(人·天)
运1吨行驶1千米需1.5元 1.5元/(吨·千米)
一、问题导入
2元/(吨·千米)表示什么?
若按此计算,运5 吨货物走4 千米需要支付多少运费?
a
b
运费和哪些量有关?如何表示?
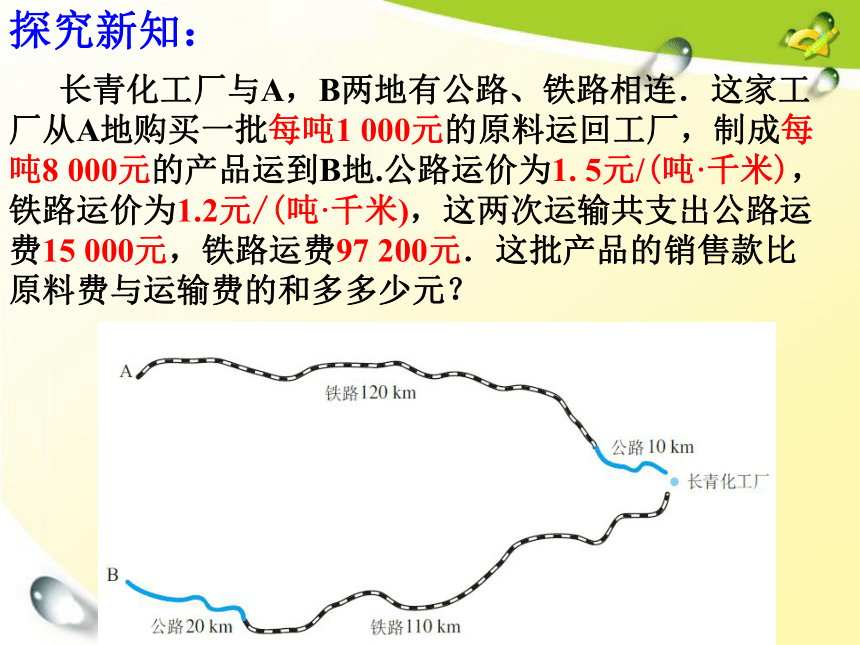
长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.公路运价为1. 5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
探究新知:
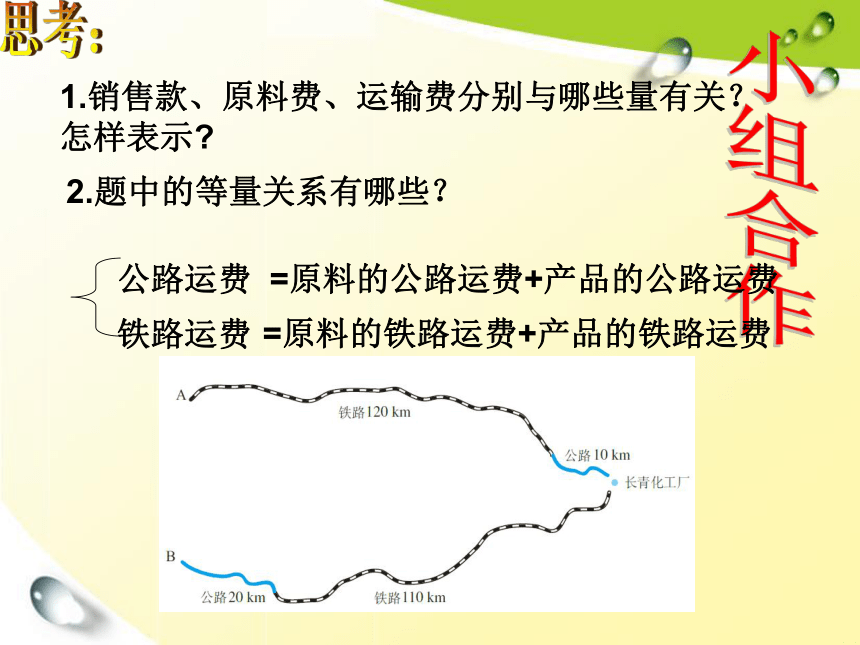
1.销售款、原料费、运输费分别与哪些量有关?
怎样表示
=原料的公路运费+产品的公路运费
=原料的铁路运费+产品的铁路运费
公路运费
铁路运费
2.题中的等量关系有哪些?
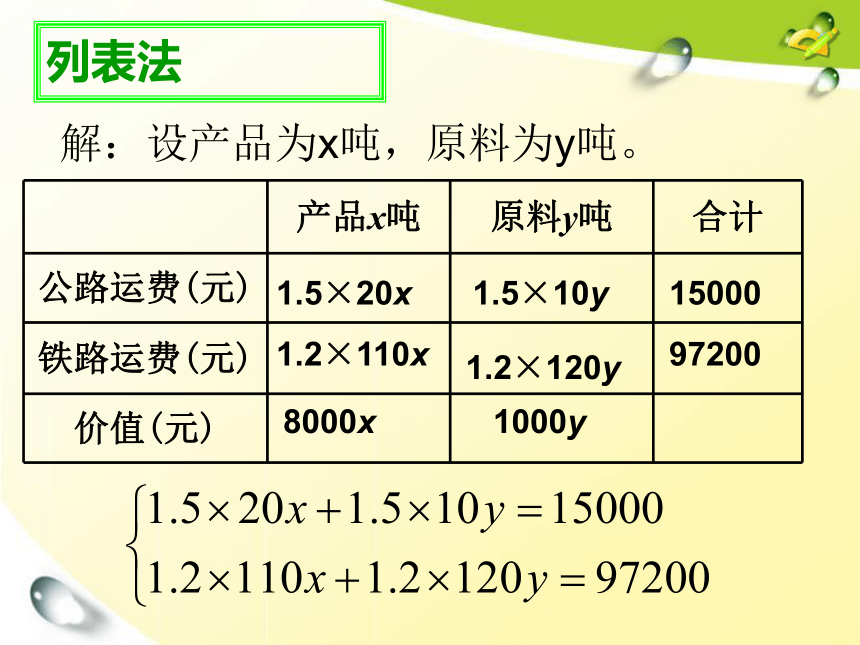
列表法
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
解:设产品为x吨,原料为y吨。
1.5×20x
1.2×110x
1.5×10y
1.2×120y
15000
97200
8000x
1000y
A
B
长青化工厂
1.2y ·120
1.5y·10
1.2x ·110
1.5x ·20
图例法
解:设产品为x吨,原料为y吨。
解得 :
销售款为:
原料费为:
运输费为:
8000X300=2400000(元)
1000X400=400000(元)
15000+97200=112200(元)
所以销售款比原料费与运输费的和多:
2400000-(400000+112200)=1887800(元)
答:销售款比原料费与运输费的和多1887800元。
解:设产品为x吨,原料为y吨。
实际问题
设未知数、列方程(组)
数学问题
二元一次方程组
解方程(组)
数学问题的解
二元一次方程组的解
检验
实际问题
的答案
(3)解决实际问题的基本过程
练一练
1.某城市规定:出租车起步价所包含的路程为0~3km,超过3km的部分按每千米另收费.
小明说:“我乘这种出租车走了11km,付了17元.”
小李说:“我乘这种出租车走了23km,付了35元.”
请你算一算:出租车的起步价是多少元?超过3km后,每千米的车费是多少元?
解 设出租车的起步价是x元,超过3km后每千米收费y元.
根据等量关系,得
解这个方程组,得
答:这种出租车的起步价是5元,
超过3km后每千米收费1.5元.
起步价 超过3km后的费用 合计费用
小明
小李
x
x
(11-3)y
(23-3)y
17
35
2.某公园的门票价格如下表所示:
某校八年级甲、乙两个班共100多人去该公园举行游园联欢活动,其中甲班有50多人,乙班不足50人。如果以班为单位分别买票,两个班一共应付920元;如果两个班联合起来作为一个团体购票,一共只要付515元。问:甲、乙两个班分别有多少人?
能力提升
请同学们结合生活中的实例,自编一道有关二元一次方程组的应用题,看谁做得又快又正确!
本节课:
你学到了什么?
谈谈你的收获…
教师寄语
同学们,今天我们学习的实际问题,都是来源于我们的生活,只要我们善于去发现,善于去思考,相信你一定有很多的收获!
新人教版初中数学七年级下册第八章
学习目标
会用列表法分析应用题中的数量关系,列出相应的二元一次方程组解决复杂的实际问题,并进一步提高解方程组的技能。
学习重点:用列表的方式分析题中的各个量的关系,列出二元一次方程组。
学习难点:从列表中获取信息,借助列表分析问题中所蕴含的数量关系。
一、问题导入
经调查,某小组6个人5天共吃了90个馒头,
问:平均每人每天吃多少个馒头?
2.把2吨货物从A地运到100千米外的B地,共支付
运费300元。问:运1吨的货物行驶1千米,需要
支付多少钱?
1人1天吃3个馒头 3个/(人·天)
运1吨行驶1千米需1.5元 1.5元/(吨·千米)
一、问题导入
2元/(吨·千米)表示什么?
若按此计算,运5 吨货物走4 千米需要支付多少运费?
a
b
运费和哪些量有关?如何表示?
长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.公路运价为1. 5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
探究新知:
1.销售款、原料费、运输费分别与哪些量有关?
怎样表示
=原料的公路运费+产品的公路运费
=原料的铁路运费+产品的铁路运费
公路运费
铁路运费
2.题中的等量关系有哪些?
列表法
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
解:设产品为x吨,原料为y吨。
1.5×20x
1.2×110x
1.5×10y
1.2×120y
15000
97200
8000x
1000y
A
B
长青化工厂
1.2y ·120
1.5y·10
1.2x ·110
1.5x ·20
图例法
解:设产品为x吨,原料为y吨。
解得 :
销售款为:
原料费为:
运输费为:
8000X300=2400000(元)
1000X400=400000(元)
15000+97200=112200(元)
所以销售款比原料费与运输费的和多:
2400000-(400000+112200)=1887800(元)
答:销售款比原料费与运输费的和多1887800元。
解:设产品为x吨,原料为y吨。
实际问题
设未知数、列方程(组)
数学问题
二元一次方程组
解方程(组)
数学问题的解
二元一次方程组的解
检验
实际问题
的答案
(3)解决实际问题的基本过程
练一练
1.某城市规定:出租车起步价所包含的路程为0~3km,超过3km的部分按每千米另收费.
小明说:“我乘这种出租车走了11km,付了17元.”
小李说:“我乘这种出租车走了23km,付了35元.”
请你算一算:出租车的起步价是多少元?超过3km后,每千米的车费是多少元?
解 设出租车的起步价是x元,超过3km后每千米收费y元.
根据等量关系,得
解这个方程组,得
答:这种出租车的起步价是5元,
超过3km后每千米收费1.5元.
起步价 超过3km后的费用 合计费用
小明
小李
x
x
(11-3)y
(23-3)y
17
35
2.某公园的门票价格如下表所示:
某校八年级甲、乙两个班共100多人去该公园举行游园联欢活动,其中甲班有50多人,乙班不足50人。如果以班为单位分别买票,两个班一共应付920元;如果两个班联合起来作为一个团体购票,一共只要付515元。问:甲、乙两个班分别有多少人?
能力提升
请同学们结合生活中的实例,自编一道有关二元一次方程组的应用题,看谁做得又快又正确!
本节课:
你学到了什么?
谈谈你的收获…
教师寄语
同学们,今天我们学习的实际问题,都是来源于我们的生活,只要我们善于去发现,善于去思考,相信你一定有很多的收获!
