人教版 八年级下册 第十七章勾股定理复习 课件(共20张PPT)
文档属性
| 名称 | 人教版 八年级下册 第十七章勾股定理复习 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 274.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 09:20:38 | ||
图片预览





文档简介
(共20张PPT)
第17章 勾股定理的复习
如果直角三角形两直角边分别为a,b,斜边为c,
那么
1、勾股定理
a2 + b2 = c2
如果三角形三边分别为a,b,c,满足
2、勾股定理逆定理
a2 + b2 = c2
那么这个三角形是直角三角形
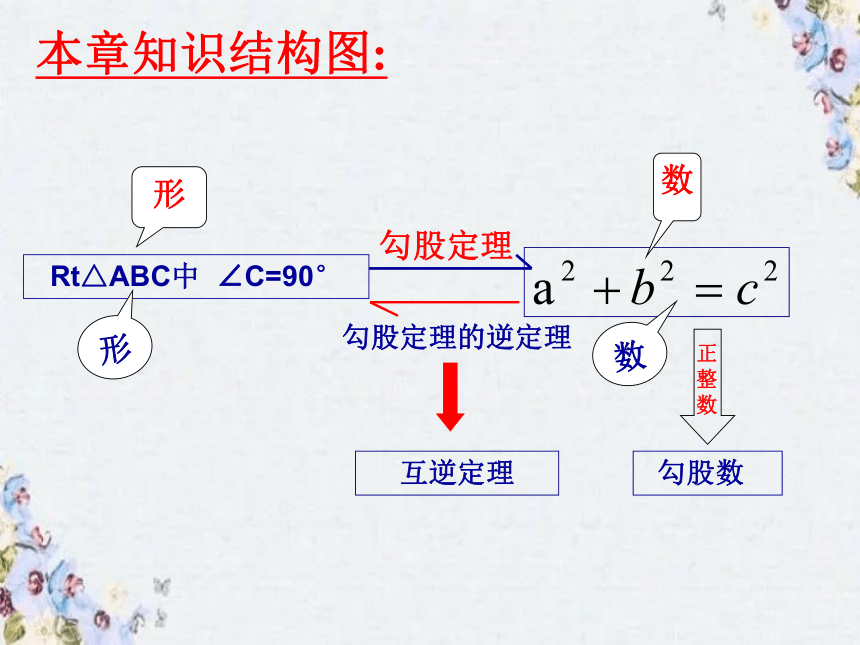
本章知识回顾
Rt△ABC中 ∠C=90°
勾股定理
形
数
勾股定理的逆定理
数
形
互逆定理
本章知识结构图:
勾股数
正整数
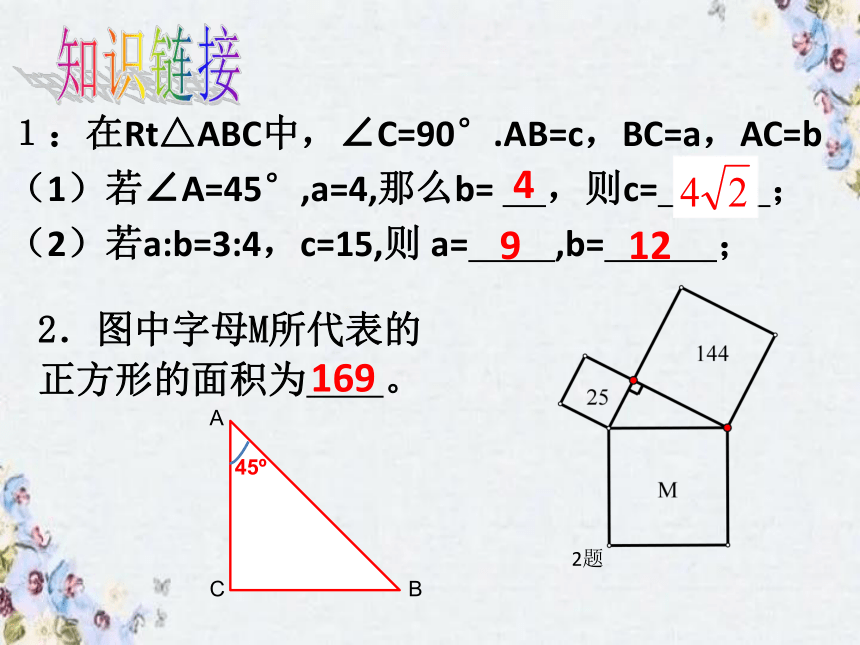
1:在Rt△ABC中,∠C=90°.AB=c,BC=a,AC=b
(1)若∠A=45°,a=4,那么b= ,则c= ;
(2)若a:b=3:4,c=15,则 a= ,b= ;
知识链接
4
9
12
2.图中字母M所代表的
正方形的面积为 。
2题
169
A
B
C
45
3.将直角三角形的三边长同时扩大2倍,得到的三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
4.“如果两个实数是正数,那么它们的积是正数。”的逆命题是_____________________________________, 这个逆命题_______(填成立或不成立)
如果两个实数的积是正数,那么它们是正数
不成立
B
重点探究内容
1.分类思想,解决直角三角形中的计算问题.
(导学案:5题和10题)
2.运用方程思想解实际问题和折叠类问题.
(导学案:6题和7题)
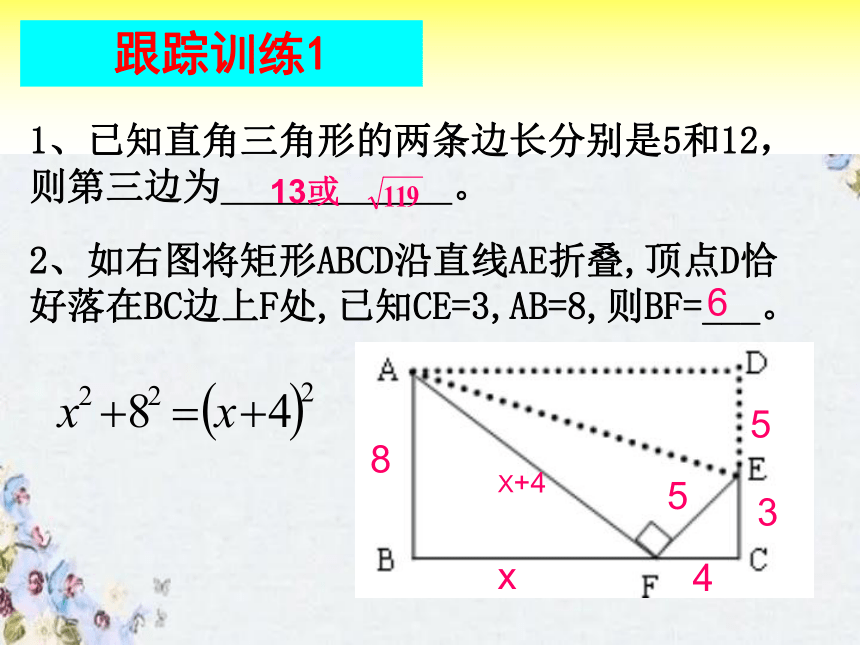
8
3
5
5
X+4
跟踪训练1
1、已知直角三角形的两条边长分别是5和12,
则第三边为 。
2、如右图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF=___。
6
13或
4
x
3、如图所示是一块地,已知∠B=900,AB=3,BC=4,CD=12,AD=13,求这块地的面积
跟踪训练2:添加辅助线
3
4
12
13
5
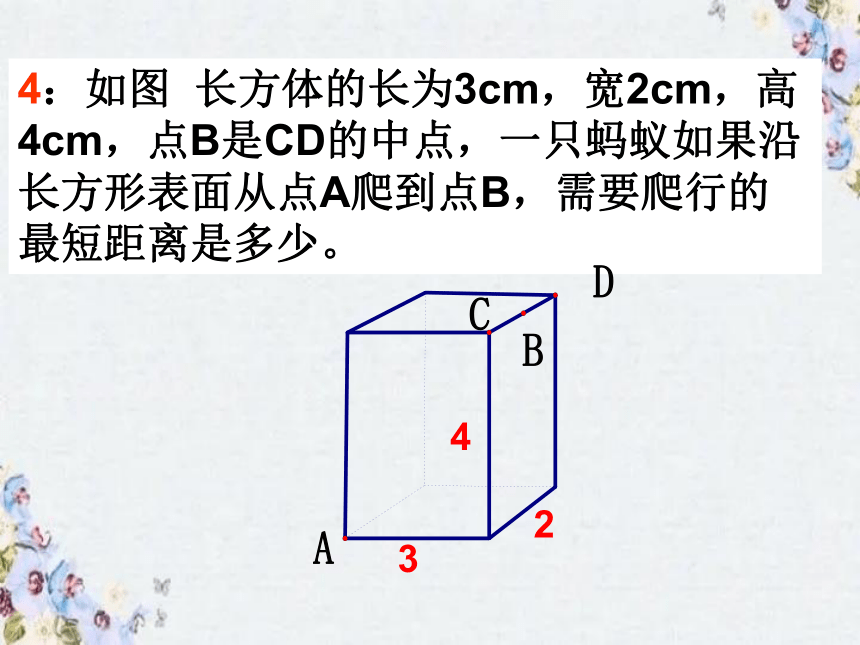
4:如图 长方体的长为3cm,宽2cm,高4cm,点B是CD的中点,一只蚂蚁如果沿长方形表面从点A爬到点B,需要爬行的最短距离是多少。
4
3
2
①沿上面和前面爬行
②沿前面和右面爬行
③沿左面和上面爬行
3
4
1
3
4
1
3
4
1
3
4
1
1
课堂练习
1.下列每一组数据中的三个数据分别为三角形的三边长,不能构成直角三角形的是( )
A.3,4,5 B.5,12,13 C. ,2,1 D.13,14,15
2.在平面直角坐标系中,已知点P的坐标是(3,4),则OP的长为 ( )
A.3 B.4 C.5 D.
3.已知直角三角形的两边长分别为6和8,则它的第三边长为 .
D
C
A
D B C
4、△ABC中,AB=10,AC=17,BC边上的高
AD=8,则BC= .
A
B D C
21
或9
分类讨论
5、如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1.0,1.21,1.44,正放置的四个正方形的面积分别为S1 、S2 、S3 、S4 ,则S1 +S2+S3 +S4 = .
A
C
B
D
E
S1+S2=AB2+DE2
=AB2+BC2
2.44
转 化
=AC2
=1
6、如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A.3 B.4
C.5 D.6
8
3
3
5
4
方 程
x
x
D
7、已知:如图,△ABC中,∠C=90°,D为AB的中点,E、F分别在AC、BC上,且DE⊥DF.
求证:AE2+BF2=EF2.
G
BG=AE
转 化
BG2+BF2
=GF2
8、在平行四边形ABCD中,BC边上的高为4,AB=5,
AC=2 ,则平行四边形ABCD的周长等于 .
A
B
H
C
D
A
B
H
C
D
20或12
9、如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,CB= ,CD= ,D为AB边上一点.求AD的长.
A
D
E
C B
10、如图,在矩形ABCD中,AB=3,BC=4,若将矩形折叠,使点C与点A重合,求折叠后的痕迹EF的长.
A E D
B F C
O
11、已知:如图,△ABC的三边长分别为AB=13,AC=15,BC=14,求△ABC的面积.
A
B C
一般三角形
直角三角形
H
转化
方程
通过本节课的学习,对今后探究线段问题有何帮助?又感悟到哪些数学思想方法?
活动四 反思学习
第17章 勾股定理的复习
如果直角三角形两直角边分别为a,b,斜边为c,
那么
1、勾股定理
a2 + b2 = c2
如果三角形三边分别为a,b,c,满足
2、勾股定理逆定理
a2 + b2 = c2
那么这个三角形是直角三角形
本章知识回顾
Rt△ABC中 ∠C=90°
勾股定理
形
数
勾股定理的逆定理
数
形
互逆定理
本章知识结构图:
勾股数
正整数
1:在Rt△ABC中,∠C=90°.AB=c,BC=a,AC=b
(1)若∠A=45°,a=4,那么b= ,则c= ;
(2)若a:b=3:4,c=15,则 a= ,b= ;
知识链接
4
9
12
2.图中字母M所代表的
正方形的面积为 。
2题
169
A
B
C
45
3.将直角三角形的三边长同时扩大2倍,得到的三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
4.“如果两个实数是正数,那么它们的积是正数。”的逆命题是_____________________________________, 这个逆命题_______(填成立或不成立)
如果两个实数的积是正数,那么它们是正数
不成立
B
重点探究内容
1.分类思想,解决直角三角形中的计算问题.
(导学案:5题和10题)
2.运用方程思想解实际问题和折叠类问题.
(导学案:6题和7题)
8
3
5
5
X+4
跟踪训练1
1、已知直角三角形的两条边长分别是5和12,
则第三边为 。
2、如右图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF=___。
6
13或
4
x
3、如图所示是一块地,已知∠B=900,AB=3,BC=4,CD=12,AD=13,求这块地的面积
跟踪训练2:添加辅助线
3
4
12
13
5
4:如图 长方体的长为3cm,宽2cm,高4cm,点B是CD的中点,一只蚂蚁如果沿长方形表面从点A爬到点B,需要爬行的最短距离是多少。
4
3
2
①沿上面和前面爬行
②沿前面和右面爬行
③沿左面和上面爬行
3
4
1
3
4
1
3
4
1
3
4
1
1
课堂练习
1.下列每一组数据中的三个数据分别为三角形的三边长,不能构成直角三角形的是( )
A.3,4,5 B.5,12,13 C. ,2,1 D.13,14,15
2.在平面直角坐标系中,已知点P的坐标是(3,4),则OP的长为 ( )
A.3 B.4 C.5 D.
3.已知直角三角形的两边长分别为6和8,则它的第三边长为 .
D
C
A
D B C
4、△ABC中,AB=10,AC=17,BC边上的高
AD=8,则BC= .
A
B D C
21
或9
分类讨论
5、如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1.0,1.21,1.44,正放置的四个正方形的面积分别为S1 、S2 、S3 、S4 ,则S1 +S2+S3 +S4 = .
A
C
B
D
E
S1+S2=AB2+DE2
=AB2+BC2
2.44
转 化
=AC2
=1
6、如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A.3 B.4
C.5 D.6
8
3
3
5
4
方 程
x
x
D
7、已知:如图,△ABC中,∠C=90°,D为AB的中点,E、F分别在AC、BC上,且DE⊥DF.
求证:AE2+BF2=EF2.
G
BG=AE
转 化
BG2+BF2
=GF2
8、在平行四边形ABCD中,BC边上的高为4,AB=5,
AC=2 ,则平行四边形ABCD的周长等于 .
A
B
H
C
D
A
B
H
C
D
20或12
9、如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,CB= ,CD= ,D为AB边上一点.求AD的长.
A
D
E
C B
10、如图,在矩形ABCD中,AB=3,BC=4,若将矩形折叠,使点C与点A重合,求折叠后的痕迹EF的长.
A E D
B F C
O
11、已知:如图,△ABC的三边长分别为AB=13,AC=15,BC=14,求△ABC的面积.
A
B C
一般三角形
直角三角形
H
转化
方程
通过本节课的学习,对今后探究线段问题有何帮助?又感悟到哪些数学思想方法?
活动四 反思学习
