人教版七年级下册第五章 平行线的判定与性质(综合复习)练习课件(共24张PPT)
文档属性
| 名称 | 人教版七年级下册第五章 平行线的判定与性质(综合复习)练习课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 847.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 09:23:01 | ||
图片预览




文档简介
(共24张PPT)
平行线的判定和性质
(复习)
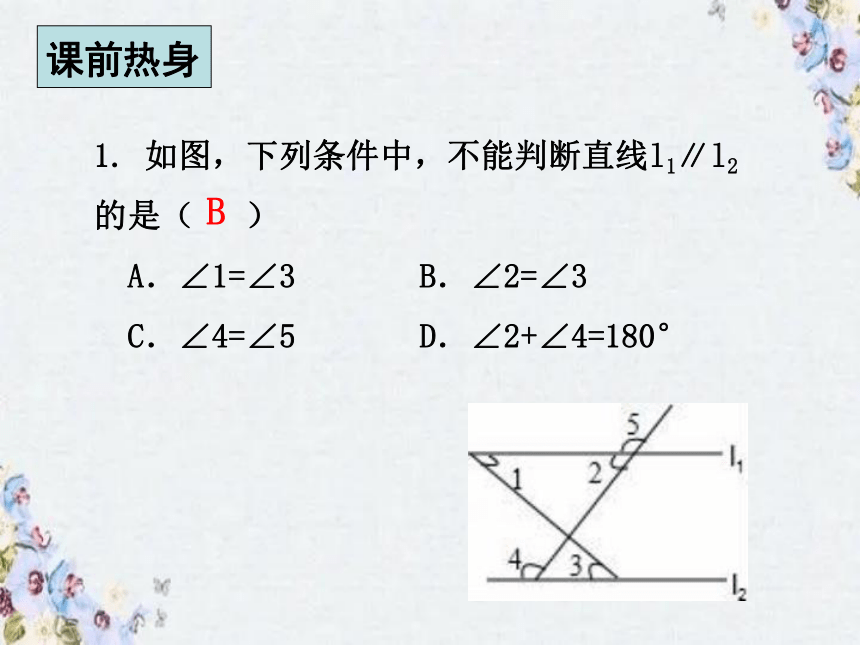
1. 如图,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠2=∠3
C.∠4=∠5 D.∠2+∠4=180°
B
课前热身
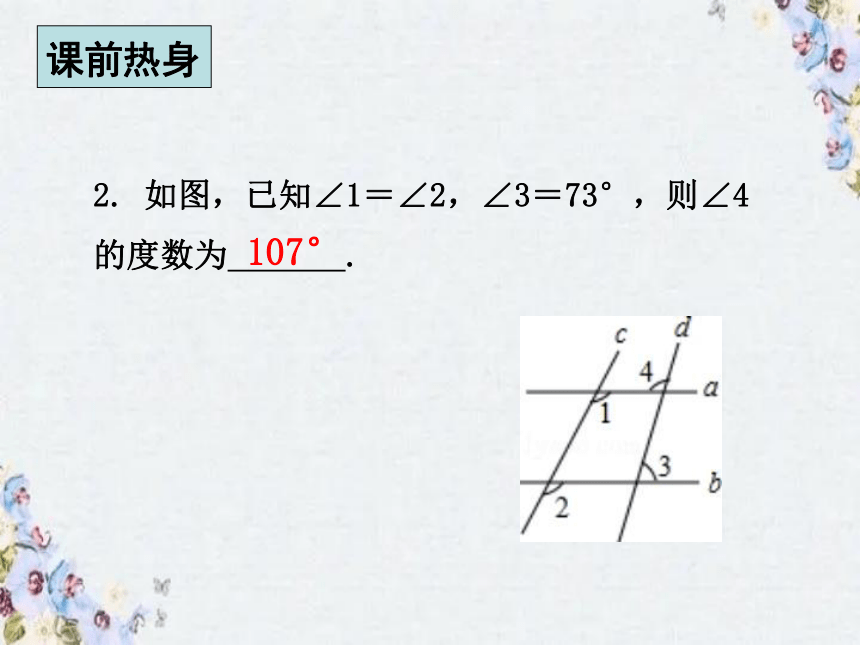
2. 如图,已知∠1=∠2,∠3=73°,则∠4的度数为 .
107°
课前热身
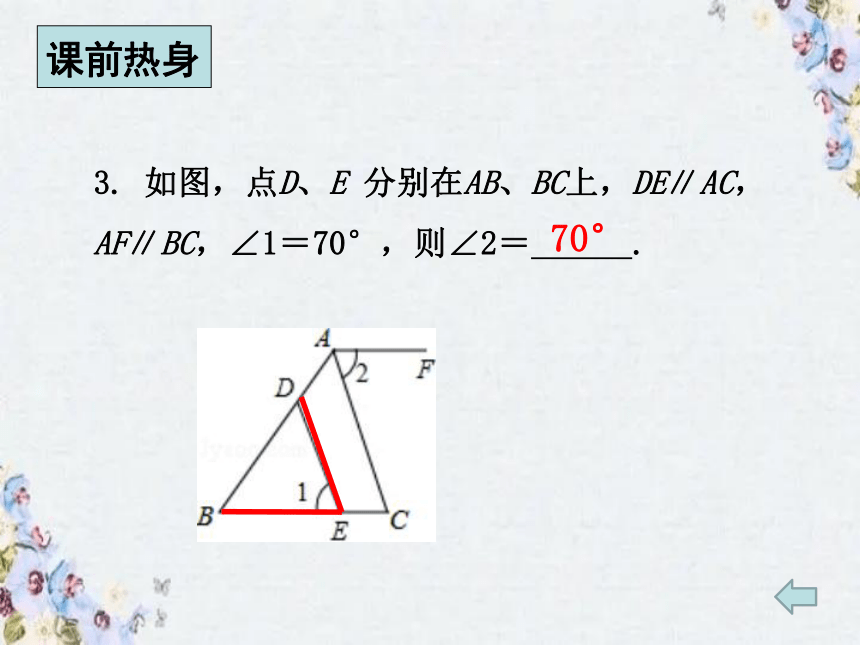
3. 如图,点D、E 分别在AB、BC上,DE∥AC,AF∥BC,∠1=70°,则∠2= .
70°
课前热身
学习目标:
1、复习平行线的判定和性质,体会几何证明的过程。
2、灵活运用平行线的判定和性质,提高分析和解决问题的能力。
3、激发学习数学的兴趣,体会合作学习的快乐与成功。
学习重点:
掌握平行线的判定和性质之间的区别与联系,灵活运用平行线的判定和性质。
学习难点:
平行线的判定和性质的灵活运用。
平行线的 . 平行线的
,两直线平行。
,两直线平行。
,两直线平行。 两直线平行, 。两直线平行, 。两直线平行, 。
特殊的
判定 于同一条直线的两条直线互相 。
于同一条直线的两条直线互相 。
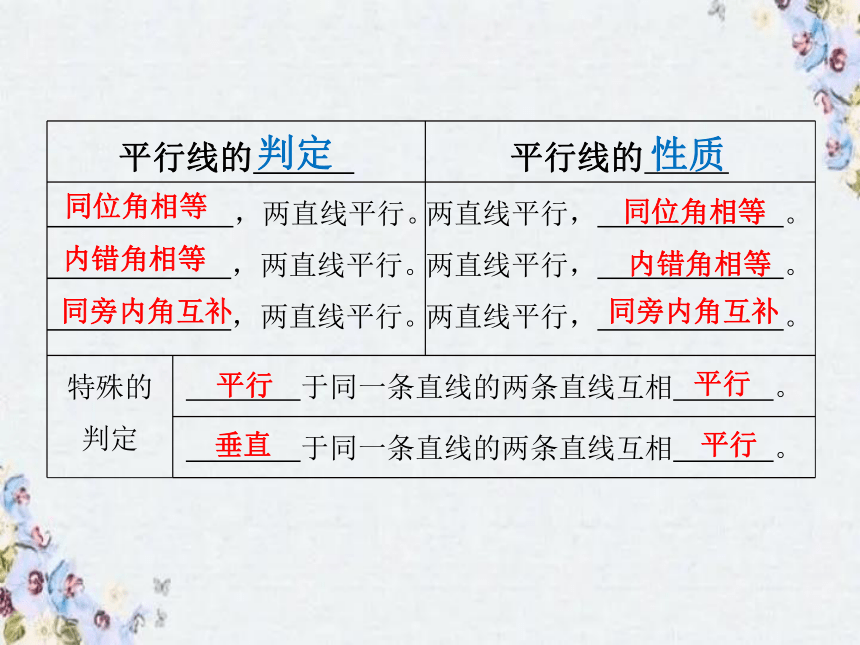
同位角相等
同位角相等
内错角相等
内错角相等
同旁内角互补
同旁内角互补
性质
判定
平行
平行
平行
垂直
例1 如图:填空,并注明理由。
AB
ED
内错角相等,两直线平行
AF
BE
同位角相等,两直线平行
AF
BE
同旁内角互补,两直线平行
AB
ED
平行于同一条直线的两条直线互相平行
A
B
C
D
E
F
1
2
3
4
5
平行线判定的应用
∵ ∠3= ∠4 (已知)
∴ ——∥——( )
∵ ∠5+ ∠AFE=180° (已知)
∴ ——∥——( )
∵ AB ∥FC, ED ∥FC (已知)
∴ ——∥——( )
∵ ∠1= ∠2 (已知)
∴ ——∥——( )
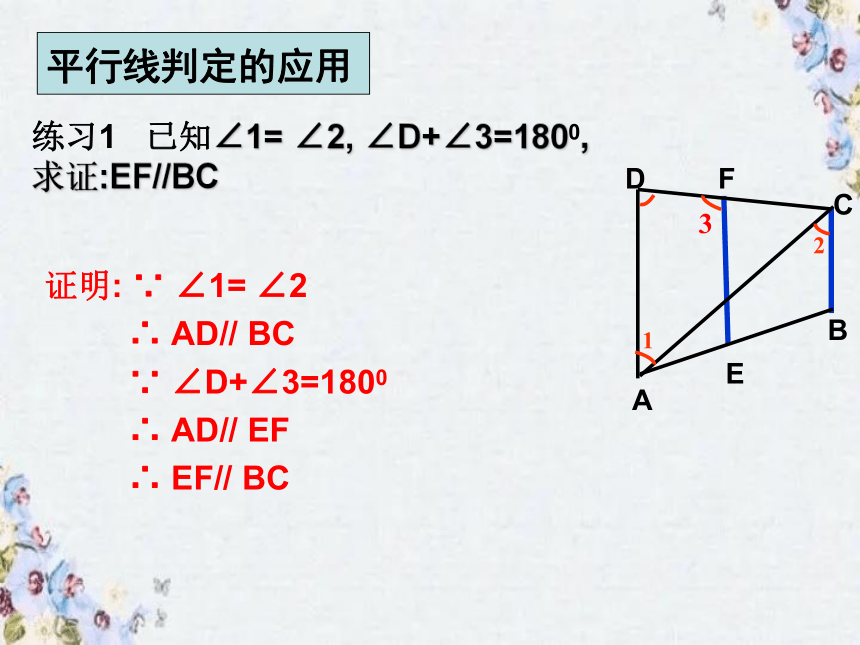
练习1 已知∠1= ∠2, ∠D+∠3=1800,
求证:EF//BC
证明: ∵ ∠1= ∠2
∴ AD// BC
∵ ∠D+∠3=1800
∴ AD// EF
∴ EF// BC
A
B
C
D
E
F
平行线判定的应用
1
2
3
例2 如图,AB∥DE∥CF,∠B=70°,∠D=130°,
求∠BCD的度数.
解:∵AB∥CF,∠B=70°
∴∠BCF=∠B=70°
∵DE∥CF,∠D=130°
∴∠DCF=180°-∠D=180°-130°=50°
∴∠BCD=∠BCF-∠DCF=70°-50°=20°
平行线性质的应用
练习2 如图,AD∥BC,EF平分∠DEG,∠EFG=55°,求∠1,∠2的度数.
解:∵AD∥BC,∠EFG=55°,
∴∠3=∠EFG=55°
∠1+∠2=180°
∵EF平分∠DEG,
∴∠4=∠3=55°.
∴∠1=180°-(∠3+∠4)
=180°-(55°+55°)=70°
∠2=180°-∠1=180°-70°=110°
平行线性质的应用
3
4
A
B
E
C
F
D
2
1
例3 如图,已知∠1=∠2,CE//BF,试说明AB//CD.
证明: ∵ CE//BF
∴ ∠C=∠2
∵ ∠1=∠2
∴ ∠1=∠C
∴ AB∥CD
平行线判定与性质的综合应用
证明: ∵ CE//BF
∴ ∠1=∠B
∵ ∠1=∠2
∴ ∠2=∠B
∴ AB∥CD
证明:∵ EF⊥AB,CD⊥AB
∴ CD∥EF
∴ ∠1=∠3
∵ ∠1=∠2
∴ ∠2=∠3
∴ DG∥BC
∴ ∠AGD=∠ACB
练习3 已知EF⊥AB,CD⊥AB,∠1=∠2,求证:
∠AGD=∠ACB.
1
2
3
平行线判定与性质的综合应用
例4 如图,AB∥CD,探索∠APC与∠A,∠C之间的关系
解:如图,过点P作PE∥AB.
∵AB∥CD,
∴PE∥CD
∴∠A+∠1=180°
∠2+∠C=180°
∴∠A+∠1+∠2+∠C=360°
∴∠A+∠APC+∠C=360°
“拐点”问题
解:如图,过点P作PE∥AB.
∵AB∥CD,
∴PE∥CD,
∴∠A=∠1,∠2=∠C.
∵∠APC=∠1+∠2,
∴∠APC=∠A+∠C.
练习4 如图,AB∥CD,探索∠APC与∠A,∠C之间的关系.
“拐点”问题
2
1
练习5 如图,将一副三角板和一张对边平行的纸条按图中方式摆放,两个三角板的一条直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
A.30° B.20° C.15° D.14°
C
“拐点”问题
①如图1,若有1个拐点,则∠B+∠P+∠D=____;
图1
图2
②如图2,若有2个拐点,则∠B+∠P+∠Q+∠D=____;
E
练习6 已知AB∥CD:
③如图3,若有3个拐点,则∠B+∠P+∠Q+∠R+∠D=____;
④如图3,若有n个拐点,则∠B+∠P+…+∠D= .
图3
图4
E
F
E
F
G
360°
540°
720°
(n+1) ·180°
“拐点”问题
课堂小结
∠1=∠4
∠2+∠4=180°
∠3=∠4
判定
性质
课堂小结
特殊的判定
,
,
作业布置
1、课本第36页复习题5 第6、13题
2、练习册《课堂感悟》 第24-26页
3、完成本学案未完成的练习
补充练习
1.如图,若直线a,b分别与直线c,d相交,且∠1+∠3=90°,∠2﹣∠3=90°,∠4=115°,那么∠3= .
65°
2. 如图,AB∥CD,且∠A=60°-α,∠APC=45°+α,∠C=30°-α,则α =( )
A、10° B、15°
C、20° D、30°
B
补充练习
3.如图,已知AB∥CD,∠1=100°,∠2=120°,则∠α= 度.
40
补充练习
4.如图,已知∠B=25°,∠BCD=45°,∠CDE=30°,∠E=10°,求证:AB∥EF.
补充练习
5.如图,AB∥ED,α=∠A+∠E,β=∠B+∠C+∠D.
证明:β=2α.
补充练习
平行线的判定和性质
(复习)
1. 如图,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠2=∠3
C.∠4=∠5 D.∠2+∠4=180°
B
课前热身
2. 如图,已知∠1=∠2,∠3=73°,则∠4的度数为 .
107°
课前热身
3. 如图,点D、E 分别在AB、BC上,DE∥AC,AF∥BC,∠1=70°,则∠2= .
70°
课前热身
学习目标:
1、复习平行线的判定和性质,体会几何证明的过程。
2、灵活运用平行线的判定和性质,提高分析和解决问题的能力。
3、激发学习数学的兴趣,体会合作学习的快乐与成功。
学习重点:
掌握平行线的判定和性质之间的区别与联系,灵活运用平行线的判定和性质。
学习难点:
平行线的判定和性质的灵活运用。
平行线的 . 平行线的
,两直线平行。
,两直线平行。
,两直线平行。 两直线平行, 。两直线平行, 。两直线平行, 。
特殊的
判定 于同一条直线的两条直线互相 。
于同一条直线的两条直线互相 。
同位角相等
同位角相等
内错角相等
内错角相等
同旁内角互补
同旁内角互补
性质
判定
平行
平行
平行
垂直
例1 如图:填空,并注明理由。
AB
ED
内错角相等,两直线平行
AF
BE
同位角相等,两直线平行
AF
BE
同旁内角互补,两直线平行
AB
ED
平行于同一条直线的两条直线互相平行
A
B
C
D
E
F
1
2
3
4
5
平行线判定的应用
∵ ∠3= ∠4 (已知)
∴ ——∥——( )
∵ ∠5+ ∠AFE=180° (已知)
∴ ——∥——( )
∵ AB ∥FC, ED ∥FC (已知)
∴ ——∥——( )
∵ ∠1= ∠2 (已知)
∴ ——∥——( )
练习1 已知∠1= ∠2, ∠D+∠3=1800,
求证:EF//BC
证明: ∵ ∠1= ∠2
∴ AD// BC
∵ ∠D+∠3=1800
∴ AD// EF
∴ EF// BC
A
B
C
D
E
F
平行线判定的应用
1
2
3
例2 如图,AB∥DE∥CF,∠B=70°,∠D=130°,
求∠BCD的度数.
解:∵AB∥CF,∠B=70°
∴∠BCF=∠B=70°
∵DE∥CF,∠D=130°
∴∠DCF=180°-∠D=180°-130°=50°
∴∠BCD=∠BCF-∠DCF=70°-50°=20°
平行线性质的应用
练习2 如图,AD∥BC,EF平分∠DEG,∠EFG=55°,求∠1,∠2的度数.
解:∵AD∥BC,∠EFG=55°,
∴∠3=∠EFG=55°
∠1+∠2=180°
∵EF平分∠DEG,
∴∠4=∠3=55°.
∴∠1=180°-(∠3+∠4)
=180°-(55°+55°)=70°
∠2=180°-∠1=180°-70°=110°
平行线性质的应用
3
4
A
B
E
C
F
D
2
1
例3 如图,已知∠1=∠2,CE//BF,试说明AB//CD.
证明: ∵ CE//BF
∴ ∠C=∠2
∵ ∠1=∠2
∴ ∠1=∠C
∴ AB∥CD
平行线判定与性质的综合应用
证明: ∵ CE//BF
∴ ∠1=∠B
∵ ∠1=∠2
∴ ∠2=∠B
∴ AB∥CD
证明:∵ EF⊥AB,CD⊥AB
∴ CD∥EF
∴ ∠1=∠3
∵ ∠1=∠2
∴ ∠2=∠3
∴ DG∥BC
∴ ∠AGD=∠ACB
练习3 已知EF⊥AB,CD⊥AB,∠1=∠2,求证:
∠AGD=∠ACB.
1
2
3
平行线判定与性质的综合应用
例4 如图,AB∥CD,探索∠APC与∠A,∠C之间的关系
解:如图,过点P作PE∥AB.
∵AB∥CD,
∴PE∥CD
∴∠A+∠1=180°
∠2+∠C=180°
∴∠A+∠1+∠2+∠C=360°
∴∠A+∠APC+∠C=360°
“拐点”问题
解:如图,过点P作PE∥AB.
∵AB∥CD,
∴PE∥CD,
∴∠A=∠1,∠2=∠C.
∵∠APC=∠1+∠2,
∴∠APC=∠A+∠C.
练习4 如图,AB∥CD,探索∠APC与∠A,∠C之间的关系.
“拐点”问题
2
1
练习5 如图,将一副三角板和一张对边平行的纸条按图中方式摆放,两个三角板的一条直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
A.30° B.20° C.15° D.14°
C
“拐点”问题
①如图1,若有1个拐点,则∠B+∠P+∠D=____;
图1
图2
②如图2,若有2个拐点,则∠B+∠P+∠Q+∠D=____;
E
练习6 已知AB∥CD:
③如图3,若有3个拐点,则∠B+∠P+∠Q+∠R+∠D=____;
④如图3,若有n个拐点,则∠B+∠P+…+∠D= .
图3
图4
E
F
E
F
G
360°
540°
720°
(n+1) ·180°
“拐点”问题
课堂小结
∠1=∠4
∠2+∠4=180°
∠3=∠4
判定
性质
课堂小结
特殊的判定
,
,
作业布置
1、课本第36页复习题5 第6、13题
2、练习册《课堂感悟》 第24-26页
3、完成本学案未完成的练习
补充练习
1.如图,若直线a,b分别与直线c,d相交,且∠1+∠3=90°,∠2﹣∠3=90°,∠4=115°,那么∠3= .
65°
2. 如图,AB∥CD,且∠A=60°-α,∠APC=45°+α,∠C=30°-α,则α =( )
A、10° B、15°
C、20° D、30°
B
补充练习
3.如图,已知AB∥CD,∠1=100°,∠2=120°,则∠α= 度.
40
补充练习
4.如图,已知∠B=25°,∠BCD=45°,∠CDE=30°,∠E=10°,求证:AB∥EF.
补充练习
5.如图,AB∥ED,α=∠A+∠E,β=∠B+∠C+∠D.
证明:β=2α.
补充练习
