人教版 七年级下册 第六章 实数 复习课件(共19张PPT)
文档属性
| 名称 | 人教版 七年级下册 第六章 实数 复习课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 560.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 09:32:36 | ||
图片预览





文档简介
(共19张PPT)
七年级下册期末复习
第六章 实数
一、确定目标,自主探究
请你带着下面的问题,复习全章的内容:
1. 平方根的概念是什么?算术平方根的概念是什么?这两个概念的区别与联系是什么?
2. 立方根的概念是什么?什么是开平方、开立方运算?乘方运算与开方运算有什么关系?
3. 无理数和有理数的区别是什么?
4. 实数由哪些数组成?实数与数轴上的点有什么关系?
5. 随着数的不断扩充,数的运算有什么发展?加法与乘法的运算律始终保持不变吗?
特殊:0的算术平方根是0。
一般地,如果一个正数x的平方等于
a,即 =a,那么这个正数x叫做a的
算术平方根。a的算术平方根记为 ,
读作“根号a”,a叫做被开方数。
a
1.算术平方根的定义:
二、合作探究,交流互动
一般地,如果一个数的平方等于a ,那么这个数就叫做a 的平方根(或二次方根).
这就是说,如果x 2 = a ,那么 x 就叫做 a 的平方根.a的平方根记为±
a
2. 平方根的定义:
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。
3.平方根的性质:
一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根,也叫做a的三次方根.记作 .
其中a是被开方数,3是根指数,符号“ ”读做“三次根号”.
3
5.立方根的性质:
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
4.立方根的定义:
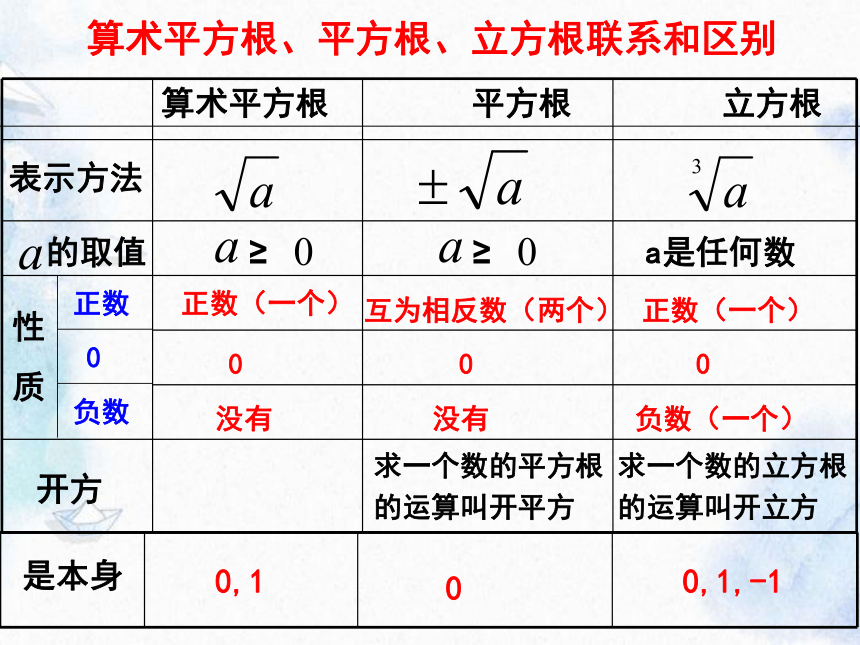
算术平方根、平方根、立方根联系和区别
算术平方根 平方根 立方根
表示方法
的取值
性
质
≥
开方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
是本身
0,1
0
0,1,-1
a是任何数
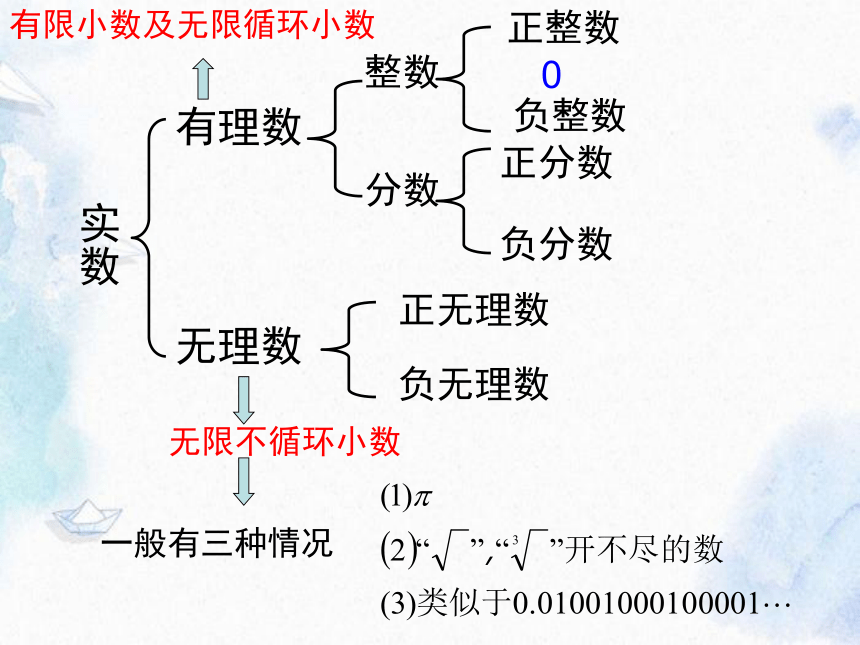
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
1. 16的平方根是_____,符号表示为_____;
16的算术平方根是____,符号表示为_____.
2. 27的立方根是____,符号表示为_____.
3
4
3.x取何值时,下列各式有意义 :
(1) (2) (3)
(x≥-4)
(X为任意实数)
(X为任意实数)
三、反馈检测,查漏补缺
4. - 5的相反数是___;- 5的绝对值是___.
5.
5
5
实数范围内相反数和绝对值
的意义与有理数范围内相同!
(1)实数不是有理数就是无理数。 ( )
(2)无限小数都是无理数。 ( )
(3)无理数都是无限小数。 ( )
(4)带根号的数都是无理数。( )
(5)两个无理数之积一定是无理数。( )
(6)所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
6.判断:下列说法是否正确:
7. 把下列各数分别填入相应的集合内:
有理数集合
无理数集合
8. 解方程
9. 计算
(1)已知: 求 的算术平方根
(2)已知x,y满足
求 的平方根
10. 解答题
=
相关知识的综合运用
三个非负性的数:
1.如果一个数的平方根为a+1和2a-7,求这个数
2.已知y= 求2(x+y)的平方根
3.已知5+ 的小数部分为m,7- 的小数部分为n,求m+n的值
4.已知满足 求a的值
综合题
1.要注意算术平方根与平方根的表示的区别
2.进行开方运算时要注意审题,即是开平方还是开立方.
3.注意
4.在解有关x的方程时,要看x是否具有实际意义,若x有意义,则一般取正数,若没有实际意义,则按平方根或立方根的定义求值.
四、课堂小结,整合知识
已知实数a、b、c,在数轴上的位置如下图所示,
试化简:
(1) -|a-b|+|c-a|+
(2)|a+b-c|+|b-2c|+
-2
五、发散思维,拓展延伸
七年级下册期末复习
第六章 实数
一、确定目标,自主探究
请你带着下面的问题,复习全章的内容:
1. 平方根的概念是什么?算术平方根的概念是什么?这两个概念的区别与联系是什么?
2. 立方根的概念是什么?什么是开平方、开立方运算?乘方运算与开方运算有什么关系?
3. 无理数和有理数的区别是什么?
4. 实数由哪些数组成?实数与数轴上的点有什么关系?
5. 随着数的不断扩充,数的运算有什么发展?加法与乘法的运算律始终保持不变吗?
特殊:0的算术平方根是0。
一般地,如果一个正数x的平方等于
a,即 =a,那么这个正数x叫做a的
算术平方根。a的算术平方根记为 ,
读作“根号a”,a叫做被开方数。
a
1.算术平方根的定义:
二、合作探究,交流互动
一般地,如果一个数的平方等于a ,那么这个数就叫做a 的平方根(或二次方根).
这就是说,如果x 2 = a ,那么 x 就叫做 a 的平方根.a的平方根记为±
a
2. 平方根的定义:
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。
3.平方根的性质:
一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根,也叫做a的三次方根.记作 .
其中a是被开方数,3是根指数,符号“ ”读做“三次根号”.
3
5.立方根的性质:
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
4.立方根的定义:
算术平方根、平方根、立方根联系和区别
算术平方根 平方根 立方根
表示方法
的取值
性
质
≥
开方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
是本身
0,1
0
0,1,-1
a是任何数
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
1. 16的平方根是_____,符号表示为_____;
16的算术平方根是____,符号表示为_____.
2. 27的立方根是____,符号表示为_____.
3
4
3.x取何值时,下列各式有意义 :
(1) (2) (3)
(x≥-4)
(X为任意实数)
(X为任意实数)
三、反馈检测,查漏补缺
4. - 5的相反数是___;- 5的绝对值是___.
5.
5
5
实数范围内相反数和绝对值
的意义与有理数范围内相同!
(1)实数不是有理数就是无理数。 ( )
(2)无限小数都是无理数。 ( )
(3)无理数都是无限小数。 ( )
(4)带根号的数都是无理数。( )
(5)两个无理数之积一定是无理数。( )
(6)所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
6.判断:下列说法是否正确:
7. 把下列各数分别填入相应的集合内:
有理数集合
无理数集合
8. 解方程
9. 计算
(1)已知: 求 的算术平方根
(2)已知x,y满足
求 的平方根
10. 解答题
=
相关知识的综合运用
三个非负性的数:
1.如果一个数的平方根为a+1和2a-7,求这个数
2.已知y= 求2(x+y)的平方根
3.已知5+ 的小数部分为m,7- 的小数部分为n,求m+n的值
4.已知满足 求a的值
综合题
1.要注意算术平方根与平方根的表示的区别
2.进行开方运算时要注意审题,即是开平方还是开立方.
3.注意
4.在解有关x的方程时,要看x是否具有实际意义,若x有意义,则一般取正数,若没有实际意义,则按平方根或立方根的定义求值.
四、课堂小结,整合知识
已知实数a、b、c,在数轴上的位置如下图所示,
试化简:
(1) -|a-b|+|c-a|+
(2)|a+b-c|+|b-2c|+
-2
五、发散思维,拓展延伸
