人教版 七年级下册 二元一次方程与实际问题 精品课件(共20张PPT)
文档属性
| 名称 | 人教版 七年级下册 二元一次方程与实际问题 精品课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 727.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 09:42:30 | ||
图片预览





文档简介
(共20张PPT)
第八章二元一次方程组的实际问题
综合应用
一、行程问题
二、工程问题
三、商品经济问题
四、配套问题
五、比例问题
一、行程问题
基本数量关系
路程=时间×速度
时间=路程/速度
速度=路程/时间
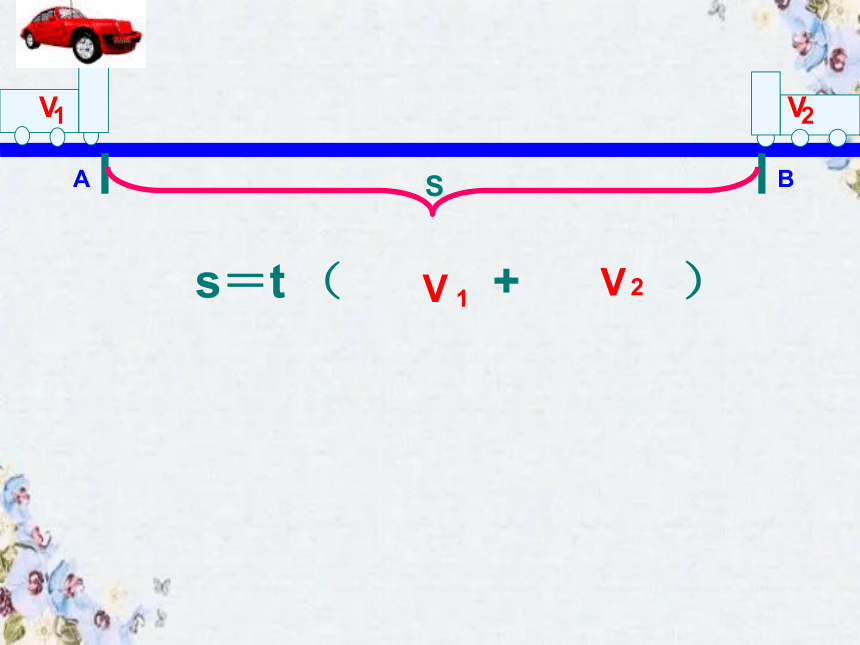
同时相向而行
路程=时间×速度之和
同时同向而行
路程=时间×速度之差
船在顺水中的速度=船在静水中的速度+水流的速度
船在逆水中的速度=船在静水中的速度-水流的速度
A
B
S
V
1
V
2
s=t ( + )
V
1
V
2
A
B
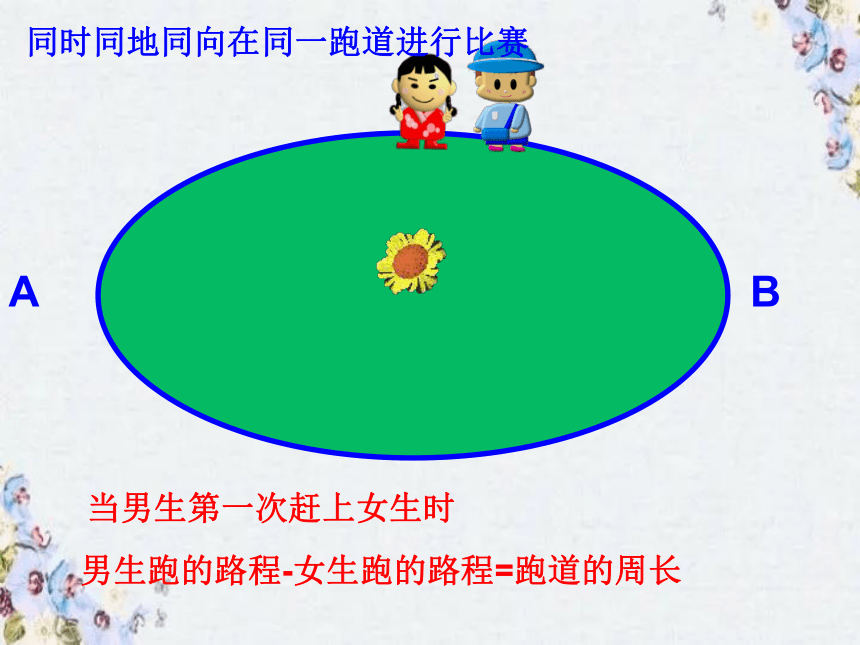
同时同地同向在同一跑道进行比赛
当男生第一次赶上女生时
男生跑的路程-女生跑的路程=跑道的周长
乙
甲
S
t
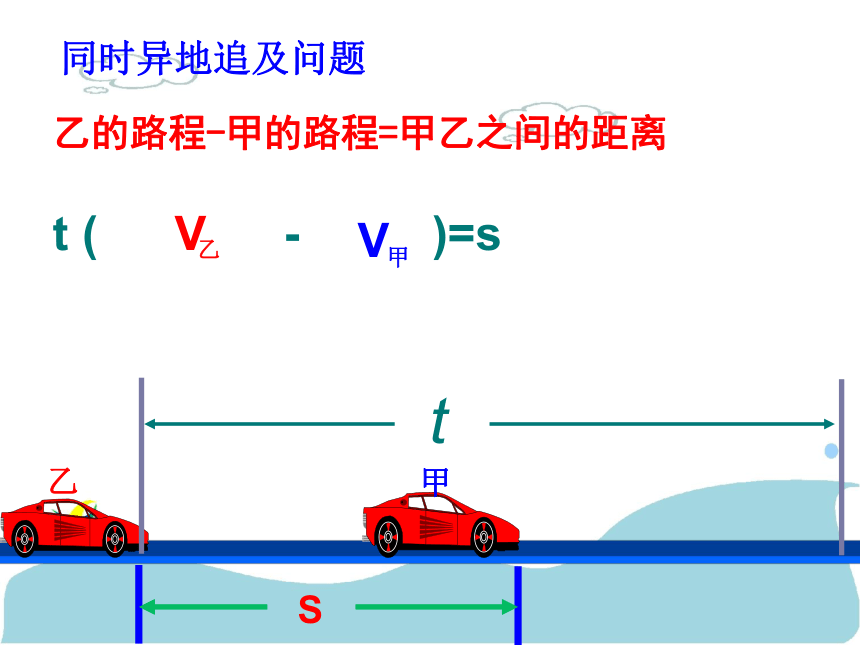
同时异地追及问题
乙的路程-甲的路程=甲乙之间的距离
t ( - )=s
V
乙
甲
V
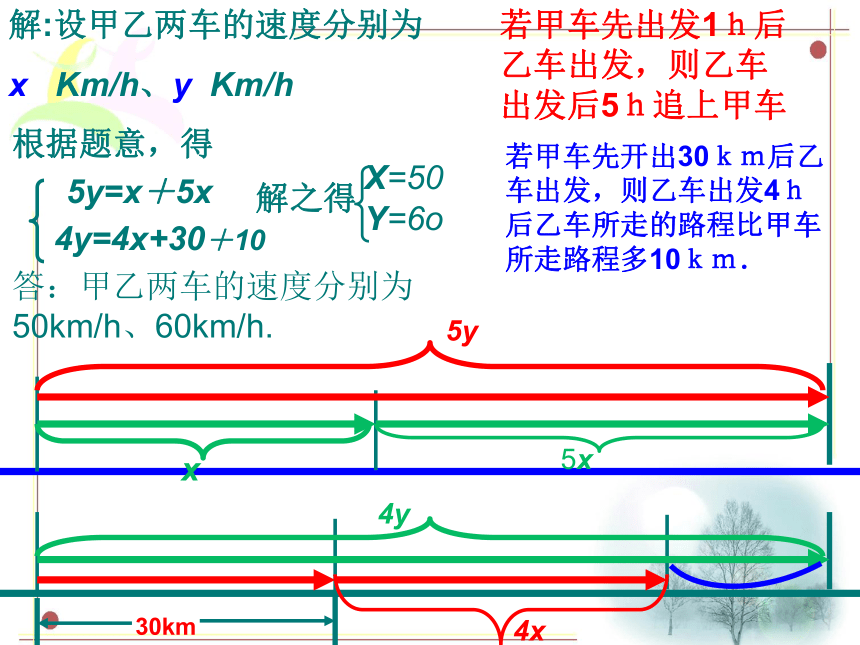
例1.某站有甲、乙两辆汽车,若甲车先出发1h后乙车出发,则乙车出发后5h追上甲车;若甲车先开出30km后乙车出发,则乙车出发4h后乙车所走的路程比甲车所走路程多10km.求两车速度.
若甲车先出发1h后乙车出发,则乙车出发后5h追上甲车
解:设甲乙两车的速度分别为
x Km/h、y Km/h
根据题意,得
x
5x
5y
5y=x+5x
若甲车先开出30km后乙车出发,则乙车出发4h后乙车所走的路程比甲车所走路程多10km.
30km
4x
4y
4y=4x+30+10
解之得
X=50
Y=6o
答:甲乙两车的速度分别为50km/h、60km/h.
例2 甲、乙两人在周长为400m的环形跑道上练跑,如果相向出发,每隔2.5min相遇一次;如果同向出发,每隔10min相遇一次,假定两人速度不变,且甲快乙慢,求甲、乙两人的速度.
甲、乙两人在周长为400m的环形跑道上练跑,如果相向出发,每隔2.5min相遇一次
解:设甲乙两人的速度分别为xm/min、ym/min
根据题意,得
A
B
2.5(x+y)=400
解:设甲乙两人的速度分别为xm/min、ym/min
根据题意,得
2.5(x+y)=400
甲、乙两人在周长为400m的环形跑道上练跑,如果同向出发,每隔10min相遇一次
甲
乙
A
10(X-Y)=400
解之得
X=100
Y=60
答:甲乙两人的速度分别为100m/min、60m/min
B
乙
甲
A
B
C
环形跑道追及问题等同于异地追及问题
例3.已知A、B两码头之间的距离为240km,一艘船航行于A、B两码头之间,顺流航行需4小时 ;逆流航行时需6小时, 求船在静水中的速度及水流的速度.
水流方向
轮船航向
船在逆水中的速度=船在
静水中的速度-水流的速度
水流方向
轮船航向
船在顺水中的速度=船在
静水中的速度+水流的速度
例3.已知A、B两码头之间的距离为240km,一艘船航行于A、B两码头之间,顺流航行需4小时 ;逆流航行时需6小时, 求船在静水中的速度及水流的速度.
解:设船在静水中的速度及水流的速度分别为xkm/h、ykm/h,根据题意,得
4(x+y)=240
6(x-y)=240
解之得
X=50
Y=10
答:船在静水中的速度及水流的速度分别为50km/h、10km/h
巩固练习
一辆汽车从甲地驶往乙地,途中要过一桥。用相同时间,若车速每小时60千米,就能越过桥2千米;若车速每小时50千米,就差3千米才到桥。问甲地与桥相距多远?用了多长时间?
课堂小结
本节课你学习了哪些内容﹖又有哪些收获﹖
谢谢﹗
第八章二元一次方程组的实际问题
综合应用
一、行程问题
二、工程问题
三、商品经济问题
四、配套问题
五、比例问题
一、行程问题
基本数量关系
路程=时间×速度
时间=路程/速度
速度=路程/时间
同时相向而行
路程=时间×速度之和
同时同向而行
路程=时间×速度之差
船在顺水中的速度=船在静水中的速度+水流的速度
船在逆水中的速度=船在静水中的速度-水流的速度
A
B
S
V
1
V
2
s=t ( + )
V
1
V
2
A
B
同时同地同向在同一跑道进行比赛
当男生第一次赶上女生时
男生跑的路程-女生跑的路程=跑道的周长
乙
甲
S
t
同时异地追及问题
乙的路程-甲的路程=甲乙之间的距离
t ( - )=s
V
乙
甲
V
例1.某站有甲、乙两辆汽车,若甲车先出发1h后乙车出发,则乙车出发后5h追上甲车;若甲车先开出30km后乙车出发,则乙车出发4h后乙车所走的路程比甲车所走路程多10km.求两车速度.
若甲车先出发1h后乙车出发,则乙车出发后5h追上甲车
解:设甲乙两车的速度分别为
x Km/h、y Km/h
根据题意,得
x
5x
5y
5y=x+5x
若甲车先开出30km后乙车出发,则乙车出发4h后乙车所走的路程比甲车所走路程多10km.
30km
4x
4y
4y=4x+30+10
解之得
X=50
Y=6o
答:甲乙两车的速度分别为50km/h、60km/h.
例2 甲、乙两人在周长为400m的环形跑道上练跑,如果相向出发,每隔2.5min相遇一次;如果同向出发,每隔10min相遇一次,假定两人速度不变,且甲快乙慢,求甲、乙两人的速度.
甲、乙两人在周长为400m的环形跑道上练跑,如果相向出发,每隔2.5min相遇一次
解:设甲乙两人的速度分别为xm/min、ym/min
根据题意,得
A
B
2.5(x+y)=400
解:设甲乙两人的速度分别为xm/min、ym/min
根据题意,得
2.5(x+y)=400
甲、乙两人在周长为400m的环形跑道上练跑,如果同向出发,每隔10min相遇一次
甲
乙
A
10(X-Y)=400
解之得
X=100
Y=60
答:甲乙两人的速度分别为100m/min、60m/min
B
乙
甲
A
B
C
环形跑道追及问题等同于异地追及问题
例3.已知A、B两码头之间的距离为240km,一艘船航行于A、B两码头之间,顺流航行需4小时 ;逆流航行时需6小时, 求船在静水中的速度及水流的速度.
水流方向
轮船航向
船在逆水中的速度=船在
静水中的速度-水流的速度
水流方向
轮船航向
船在顺水中的速度=船在
静水中的速度+水流的速度
例3.已知A、B两码头之间的距离为240km,一艘船航行于A、B两码头之间,顺流航行需4小时 ;逆流航行时需6小时, 求船在静水中的速度及水流的速度.
解:设船在静水中的速度及水流的速度分别为xkm/h、ykm/h,根据题意,得
4(x+y)=240
6(x-y)=240
解之得
X=50
Y=10
答:船在静水中的速度及水流的速度分别为50km/h、10km/h
巩固练习
一辆汽车从甲地驶往乙地,途中要过一桥。用相同时间,若车速每小时60千米,就能越过桥2千米;若车速每小时50千米,就差3千米才到桥。问甲地与桥相距多远?用了多长时间?
课堂小结
本节课你学习了哪些内容﹖又有哪些收获﹖
谢谢﹗
