沪科版数学八年级下册 18.1 勾股定理-课件(共16张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 18.1 勾股定理-课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-04 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
18.1 勾股定理
18.1.1 勾股定理的发现与证明
印度数学家什迦逻曾提出过“荷花问题”:平平湖水清可鉴,面上半尺生红莲。出泥不染亭亭立,忽被强风吹一边。渔人观看忙向前,花离原位二尺远。能算诸君请解题,湖水如何知深浅
D
2尺
C
0.5尺
A
B
转化为数学问题:
如图,已知点D在线段AB上,AD=0.5,∠BDC=90°,AB=CB,CD=2,求BD的长.
提出问题
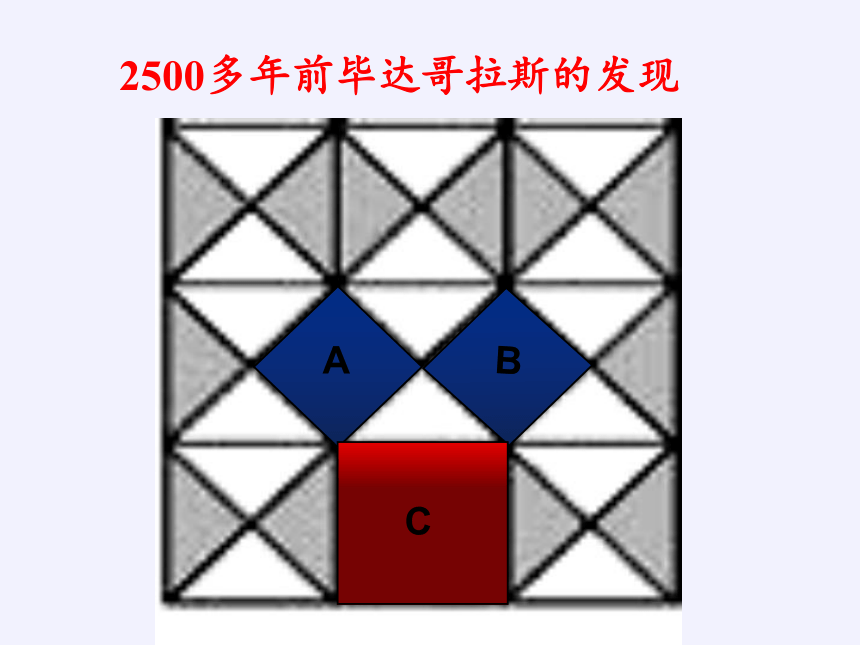
2500多年前毕达哥拉斯的发现
A
B
C
(图中每个小方格是1个单位面积)
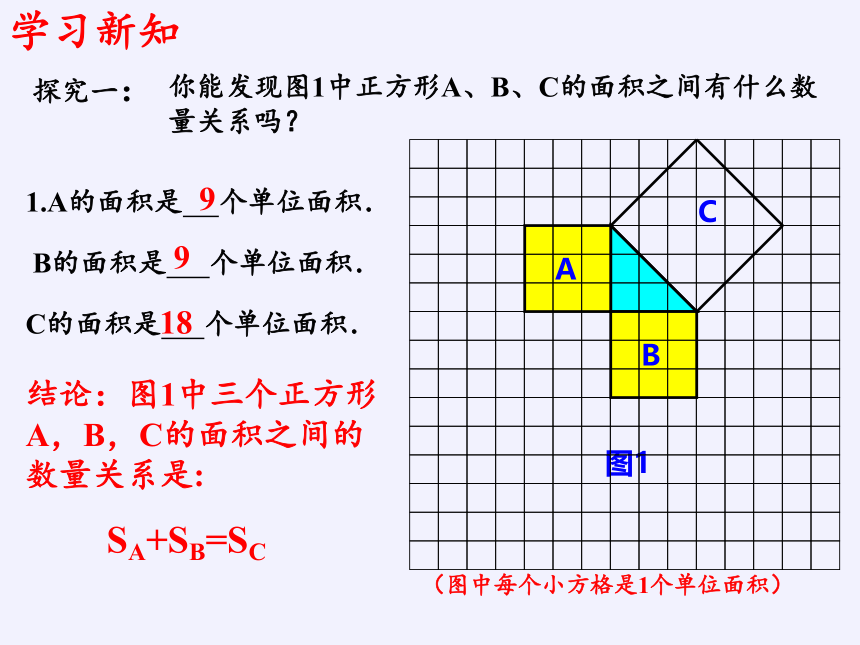
1.A的面积是 个单位面积.
B的面积是 个单位面积.
C的面积是 个单位面积.
9
18
9
探究一:
学习新知
A
B
C
图1
结论:图1中三个正方形A,B,C的面积之间的数量关系是:
SA+SB=SC
你能发现图1中正方形A、B、C的面积之间有什么数量关系吗?
探究二:
A
B
C
图2
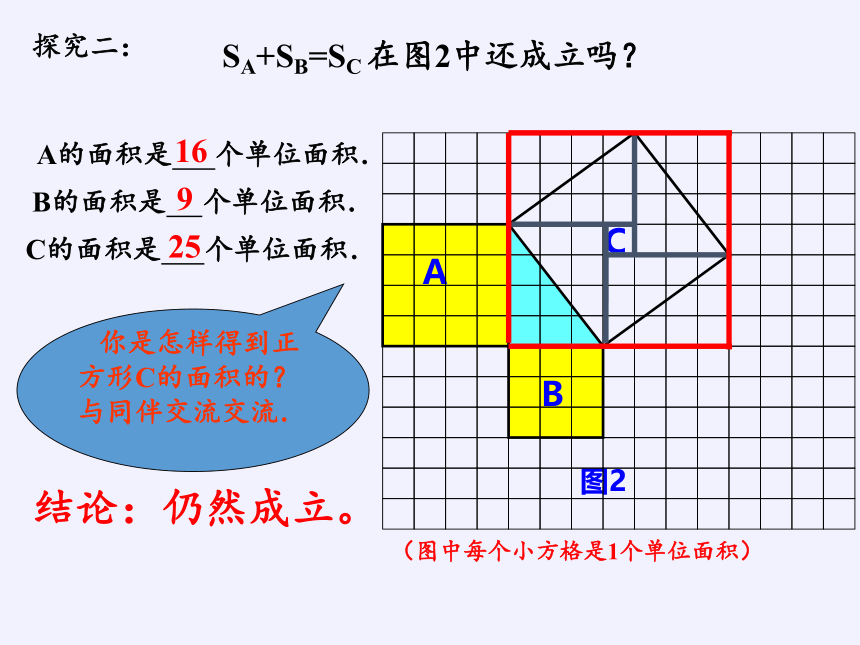
结论:仍然成立。
A的面积是 个单位面积.
B的面积是 个单位面积.
C的面积是 个单位面积.
25
16
9
你是怎样得到正方形C的面积的?与同伴交流交流.
(图中每个小方格是1个单位面积)
SA+SB=SC 在图2中还成立吗?
A
B
C
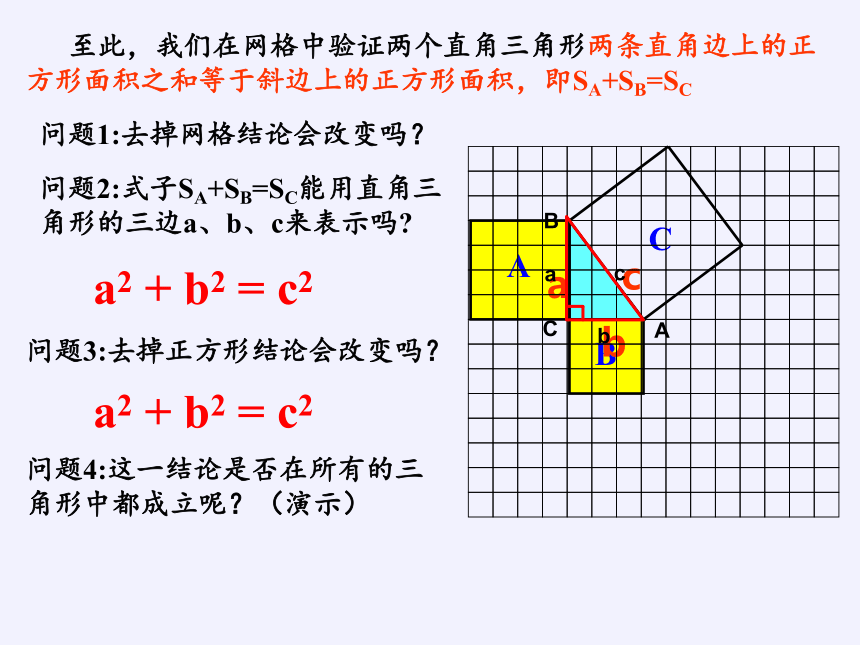
问题2:式子SA+SB=SC能用直角三角形的三边a、b、c来表示吗
a
b
c
至此,我们在网格中验证两个直角三角形两条直角边上的正方形面积之和等于斜边上的正方形面积,即SA+SB=SC
a2 + b2 = c2
a2 + b2 = c2
问题1:去掉网格结论会改变吗?
问题3:去掉正方形结论会改变吗?
问题4:这一结论是否在所有的三
角形中都成立呢?(演示)
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
a
b
c
猜想:
请各位同学拿出事先准备好的四块全等的直角三角形。你们能够利用手中的三角形采用拼图求图形面积的方法来说明你的猜想吗?
动手试一试
a
b
c
a
b
c
a
b
c
a
b
c
=
c
b
a
勾股定理:如果直角三角形两直角边长分别为a、b,斜边长为c,那么
a2 + b2 = c2
即:直角三角形两直角边的平方和等于斜边的平方。
印度数学家什迦逻曾提出过“荷花问题”:平平湖水清可鉴,面上半尺生红莲。出泥不染亭亭立,忽被强风吹一边。渔人观看忙向前,花离原位二尺远。能算诸君请解题,湖水如何知深浅
D
2尺
C
0.5尺
A
B
转化为数学问题:
如图,已知点D在线段AB上,AD=0.5,∠BDC=90°,AB=CB,CD=2,求BD的长.
解决问题
学了本节课后我们有哪些收获?
感悟收获
勾股定理其他证法
1.必做题:
课本第55页,练习第1题;
2.选做题:
上网查阅了解勾股定理的有关知识并写一篇小论文.
课后作业
说不定你也可以发现一种新的证明方法呢!
求出下列直角三角形中未知边的长度.
解:(1)在Rt△ABC中,由勾股定理得:AC2+BC2=AB2
x2+36 =100
x2 =64
x2+62=10
∵x>0
52+122=x2
x2=25+144
x2=169
∴ x=13
(2)在Rt△ABC中,由勾股定理得:AC2+BC2=AB2
∵x>0
A
6
x
10
C
B
5
12
x
C
A
B
∴x=8
实践应用
方法总结:利用勾股定理建立方程.
谢 谢
18.1 勾股定理
18.1.1 勾股定理的发现与证明
印度数学家什迦逻曾提出过“荷花问题”:平平湖水清可鉴,面上半尺生红莲。出泥不染亭亭立,忽被强风吹一边。渔人观看忙向前,花离原位二尺远。能算诸君请解题,湖水如何知深浅
D
2尺
C
0.5尺
A
B
转化为数学问题:
如图,已知点D在线段AB上,AD=0.5,∠BDC=90°,AB=CB,CD=2,求BD的长.
提出问题
2500多年前毕达哥拉斯的发现
A
B
C
(图中每个小方格是1个单位面积)
1.A的面积是 个单位面积.
B的面积是 个单位面积.
C的面积是 个单位面积.
9
18
9
探究一:
学习新知
A
B
C
图1
结论:图1中三个正方形A,B,C的面积之间的数量关系是:
SA+SB=SC
你能发现图1中正方形A、B、C的面积之间有什么数量关系吗?
探究二:
A
B
C
图2
结论:仍然成立。
A的面积是 个单位面积.
B的面积是 个单位面积.
C的面积是 个单位面积.
25
16
9
你是怎样得到正方形C的面积的?与同伴交流交流.
(图中每个小方格是1个单位面积)
SA+SB=SC 在图2中还成立吗?
A
B
C
问题2:式子SA+SB=SC能用直角三角形的三边a、b、c来表示吗
a
b
c
至此,我们在网格中验证两个直角三角形两条直角边上的正方形面积之和等于斜边上的正方形面积,即SA+SB=SC
a2 + b2 = c2
a2 + b2 = c2
问题1:去掉网格结论会改变吗?
问题3:去掉正方形结论会改变吗?
问题4:这一结论是否在所有的三
角形中都成立呢?(演示)
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
a
b
c
猜想:
请各位同学拿出事先准备好的四块全等的直角三角形。你们能够利用手中的三角形采用拼图求图形面积的方法来说明你的猜想吗?
动手试一试
a
b
c
a
b
c
a
b
c
a
b
c
=
c
b
a
勾股定理:如果直角三角形两直角边长分别为a、b,斜边长为c,那么
a2 + b2 = c2
即:直角三角形两直角边的平方和等于斜边的平方。
印度数学家什迦逻曾提出过“荷花问题”:平平湖水清可鉴,面上半尺生红莲。出泥不染亭亭立,忽被强风吹一边。渔人观看忙向前,花离原位二尺远。能算诸君请解题,湖水如何知深浅
D
2尺
C
0.5尺
A
B
转化为数学问题:
如图,已知点D在线段AB上,AD=0.5,∠BDC=90°,AB=CB,CD=2,求BD的长.
解决问题
学了本节课后我们有哪些收获?
感悟收获
勾股定理其他证法
1.必做题:
课本第55页,练习第1题;
2.选做题:
上网查阅了解勾股定理的有关知识并写一篇小论文.
课后作业
说不定你也可以发现一种新的证明方法呢!
求出下列直角三角形中未知边的长度.
解:(1)在Rt△ABC中,由勾股定理得:AC2+BC2=AB2
x2+36 =100
x2 =64
x2+62=10
∵x>0
52+122=x2
x2=25+144
x2=169
∴ x=13
(2)在Rt△ABC中,由勾股定理得:AC2+BC2=AB2
∵x>0
A
6
x
10
C
B
5
12
x
C
A
B
∴x=8
实践应用
方法总结:利用勾股定理建立方程.
谢 谢
