沪科版数学八年级下册 18.1 勾股定理课件(共16张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 18.1 勾股定理课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 756.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-04 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
18.1 勾股定理
锐角三角形
直角三角形
钝角三角形
b
a
c
a
b
c
b
a
c
在一般三角形中,三边存在什么样的关系?
想一想
相传两千五百年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映了直角三角形三边的某种数量关系,同学们,我们也来观察左面的图案,看看能发现什么?
看 一 看
相传两千五百年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映了直角三角形三边的某种数量关系,同学们,我们也来观察左面的图案,看看能发现什么?
看 一 看
(图中每个小方格是1个单位面积)
A中含有____个小方格,即A的面积是 个单位面积.
B的面积是 个单位面积.
C的面积是 个单位面积.
9
9
18
9
实验:【探究一】
A
B
C
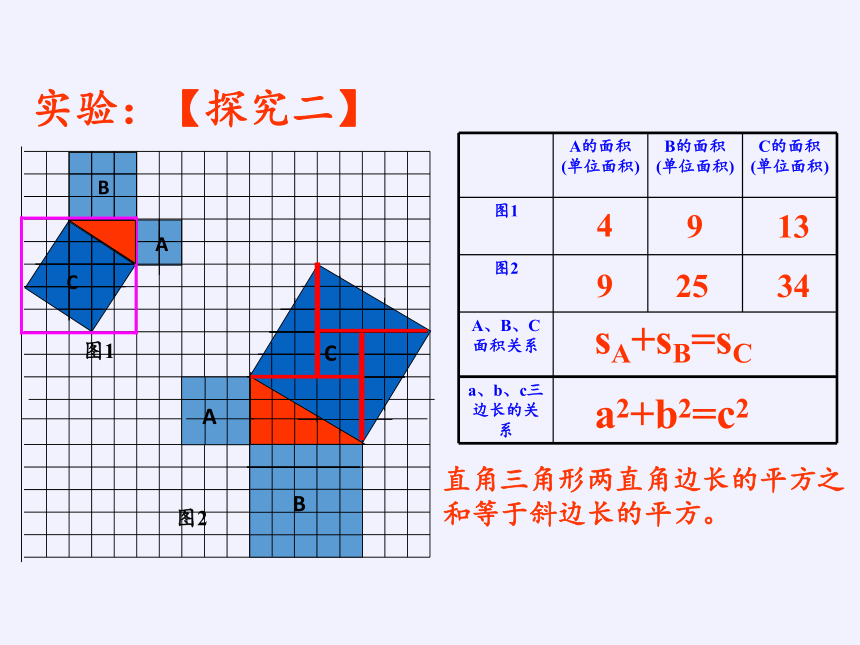
结论:图1中三个正方形A,B,C的面积之间的数量关系是:
SA+SB=SC
三个正方形A,B,C 的面积有什么关系?
A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)
图1
图2
A、B、C面积关系
a、b、c三边长的关系
4
9
13
9
25
34
sA+sB=sC
A
B
C
A
B
C
图1
图2
a2+b2=c2
直角三角形两直角边长的平方之和等于斜边长的平方。
实验:【探究二】
由此,我们猜想出:
大胆猜想
a
b
c
如果直角三角形两直角边长分别为a,b, 斜边长为c,那么 a2 + b2 = c2.
命题:
c
a
b
1、拿出准备好的四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,斜边c);
2、你能用这四个直角三角形拼成一个正方形吗?拼一拼
3、你拼的正方形中是否含有以斜边c或以(a+b)为边长的正方形?
4、你能否就你拼出的图说明a2+b2=c2?
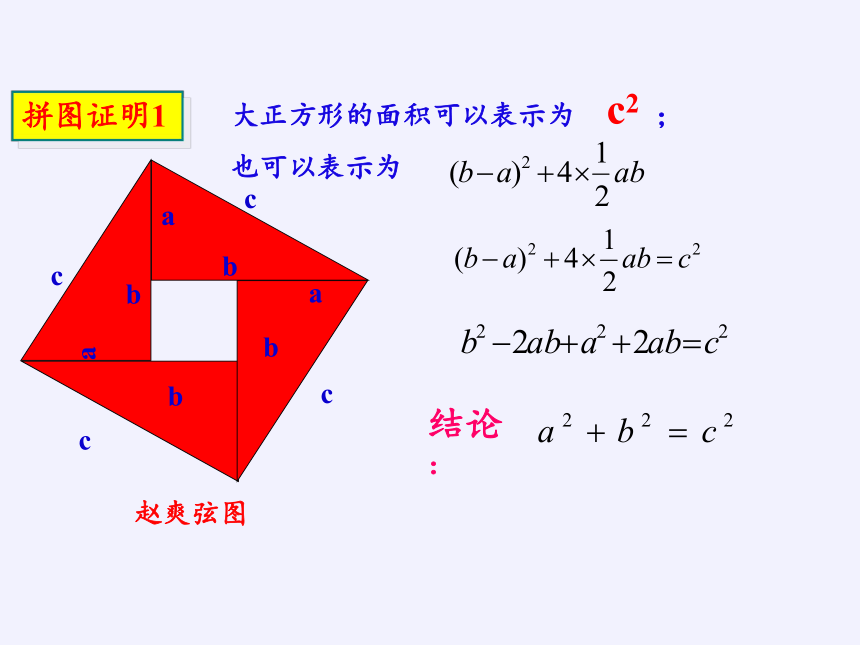
拼图证明
结论:
大正方形的面积可以表示为 ;
也可以表示为
c2
拼图证明1
c
a
b
c
b
a
c
a
b
c
a
b
赵爽弦图
可得: a2 + b2 = c2
思考:大正方形面积怎么求?
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
拼图证明2
c
a
b
c
a
b
c
a
b
c
a
b
毕达哥拉斯拼图
锐角三角形
直角三角形
钝角三角形
b
a
c
a
b
c
b
a
c
a2+b2=c2
a2+b2>c2
a2+b2继续探究
1.成立条件: 在直角三角形中;
3.作用:已知直角三角形任意两边长,求第三边长.
2.公式变形:
a
b
c
如果直角三角形两直角边长分别为a、b,斜边长为c,那么
勾 股 定 理
(注意:哪条边是斜边)
为什么叫勾股定理这个名称呢?
股
勾
弦
较
短
直
角
边
较长直角边
25OO年前,在西方,因为是毕达哥拉斯最先发现这个定理的,所以西方人通常称勾股定理为“毕达哥拉斯定理” .
我国是最早了解勾股定理的国家之一。早在3000多年前,周朝数学家商高就曾提出, “勾三、股四、弦五”,所以勾股定理又叫“商高定理”
勾股世界
例1.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,求图中直角三角形的边AC的长度。
解:在Rt△ABC中,∠ABC=90°,
根据勾股定理得,
AC2=AB2+BC2
=82+62
=100
= 10
∵AC > 0 ∴AC =
B
A
C
1.在Rt△ABC中,∠C=90 ,AB=5,AC=3,求BC的长?
3
5
A
B
C
2.在一个直角三角形中,两边长分别为4、5,求第三边长为多少?
勾股定理运用1
1
基本知识
1
基本技能
2
数学思想
3
勾股定理
4
数学方法
课堂小结
数学文化
5
拼图:赵爽弦图;毕达哥拉斯拼图
数形结合;由特殊到一般
观察、探索、猜想、验证、归纳、应用
勾股定理的历史
必做题:1.《教材》P28 第1题、第7题
2.自学课本P25-26
选做题:
(1)课本第71页“阅读与思考”,了解勾股定理的多种证法.
(2)有兴趣的学生上网查阅了解勾股定理的有关知识并写一篇小论文.
说不定你也可以创造一种新的证明方法呢!
课后作业
拓展延伸:
美国第二十任总统证法拼图
a
D
b
C
c
a
b
c
A
B
E
1
1
美丽的勾股树
谢 谢
18.1 勾股定理
锐角三角形
直角三角形
钝角三角形
b
a
c
a
b
c
b
a
c
在一般三角形中,三边存在什么样的关系?
想一想
相传两千五百年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映了直角三角形三边的某种数量关系,同学们,我们也来观察左面的图案,看看能发现什么?
看 一 看
相传两千五百年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映了直角三角形三边的某种数量关系,同学们,我们也来观察左面的图案,看看能发现什么?
看 一 看
(图中每个小方格是1个单位面积)
A中含有____个小方格,即A的面积是 个单位面积.
B的面积是 个单位面积.
C的面积是 个单位面积.
9
9
18
9
实验:【探究一】
A
B
C
结论:图1中三个正方形A,B,C的面积之间的数量关系是:
SA+SB=SC
三个正方形A,B,C 的面积有什么关系?
A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)
图1
图2
A、B、C面积关系
a、b、c三边长的关系
4
9
13
9
25
34
sA+sB=sC
A
B
C
A
B
C
图1
图2
a2+b2=c2
直角三角形两直角边长的平方之和等于斜边长的平方。
实验:【探究二】
由此,我们猜想出:
大胆猜想
a
b
c
如果直角三角形两直角边长分别为a,b, 斜边长为c,那么 a2 + b2 = c2.
命题:
c
a
b
1、拿出准备好的四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,斜边c);
2、你能用这四个直角三角形拼成一个正方形吗?拼一拼
3、你拼的正方形中是否含有以斜边c或以(a+b)为边长的正方形?
4、你能否就你拼出的图说明a2+b2=c2?
拼图证明
结论:
大正方形的面积可以表示为 ;
也可以表示为
c2
拼图证明1
c
a
b
c
b
a
c
a
b
c
a
b
赵爽弦图
可得: a2 + b2 = c2
思考:大正方形面积怎么求?
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
拼图证明2
c
a
b
c
a
b
c
a
b
c
a
b
毕达哥拉斯拼图
锐角三角形
直角三角形
钝角三角形
b
a
c
a
b
c
b
a
c
a2+b2=c2
a2+b2>c2
a2+b2
1.成立条件: 在直角三角形中;
3.作用:已知直角三角形任意两边长,求第三边长.
2.公式变形:
a
b
c
如果直角三角形两直角边长分别为a、b,斜边长为c,那么
勾 股 定 理
(注意:哪条边是斜边)
为什么叫勾股定理这个名称呢?
股
勾
弦
较
短
直
角
边
较长直角边
25OO年前,在西方,因为是毕达哥拉斯最先发现这个定理的,所以西方人通常称勾股定理为“毕达哥拉斯定理” .
我国是最早了解勾股定理的国家之一。早在3000多年前,周朝数学家商高就曾提出, “勾三、股四、弦五”,所以勾股定理又叫“商高定理”
勾股世界
例1.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,求图中直角三角形的边AC的长度。
解:在Rt△ABC中,∠ABC=90°,
根据勾股定理得,
AC2=AB2+BC2
=82+62
=100
= 10
∵AC > 0 ∴AC =
B
A
C
1.在Rt△ABC中,∠C=90 ,AB=5,AC=3,求BC的长?
3
5
A
B
C
2.在一个直角三角形中,两边长分别为4、5,求第三边长为多少?
勾股定理运用1
1
基本知识
1
基本技能
2
数学思想
3
勾股定理
4
数学方法
课堂小结
数学文化
5
拼图:赵爽弦图;毕达哥拉斯拼图
数形结合;由特殊到一般
观察、探索、猜想、验证、归纳、应用
勾股定理的历史
必做题:1.《教材》P28 第1题、第7题
2.自学课本P25-26
选做题:
(1)课本第71页“阅读与思考”,了解勾股定理的多种证法.
(2)有兴趣的学生上网查阅了解勾股定理的有关知识并写一篇小论文.
说不定你也可以创造一种新的证明方法呢!
课后作业
拓展延伸:
美国第二十任总统证法拼图
a
D
b
C
c
a
b
c
A
B
E
1
1
美丽的勾股树
谢 谢
