沪科版物理八年级全一册 第5章 质量与密度第4节 密度知识的 应用-课件(共21张PPT)
文档属性
| 名称 | 沪科版物理八年级全一册 第5章 质量与密度第4节 密度知识的 应用-课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 162.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-06-04 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
第5章 质量与密度
第4节 密度知识的应用
关于密度,你有哪些了解
密度是物质的一种特性,不同物质的密度一般不同,知道了物质的密度就能确认是哪种物质了.
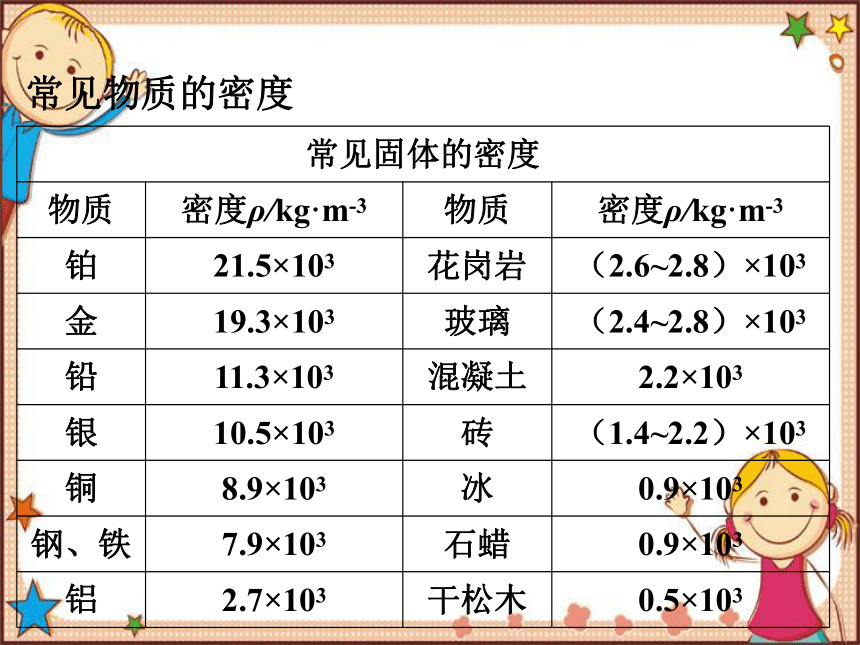
常见物质的密度
常见固体的密度
物质 密度ρ/kg·m-3 物质 密度ρ/kg·m-3
铂 21.5×103 花岗岩 (2.6~2.8)×103
金 19.3×103 玻璃 (2.4~2.8)×103
铅 11.3×103 混凝土 2.2×103
银 10.5×103 砖 (1.4~2.2)×103
铜 8.9×103 冰 0.9×103
钢、铁 7.9×103 石蜡 0.9×103
铝 2.7×103 干松木 0.5×103
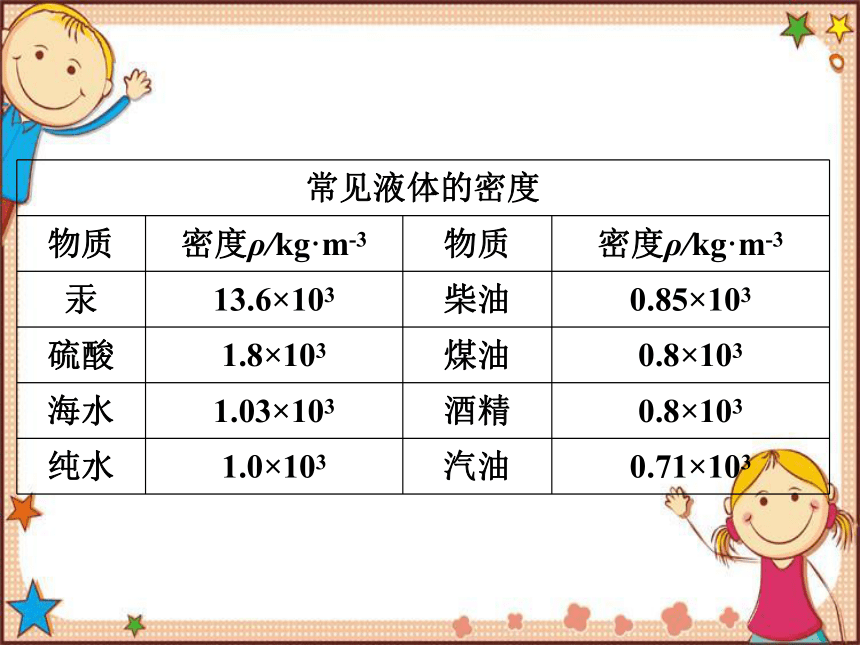
常见液体的密度
物质 密度ρ/kg·m-3 物质 密度ρ/kg·m-3
汞 13.6×103 柴油 0.85×103
硫酸 1.8×103 煤油 0.8×103
海水 1.03×103 酒精 0.8×103
纯水 1.0×103 汽油 0.71×103
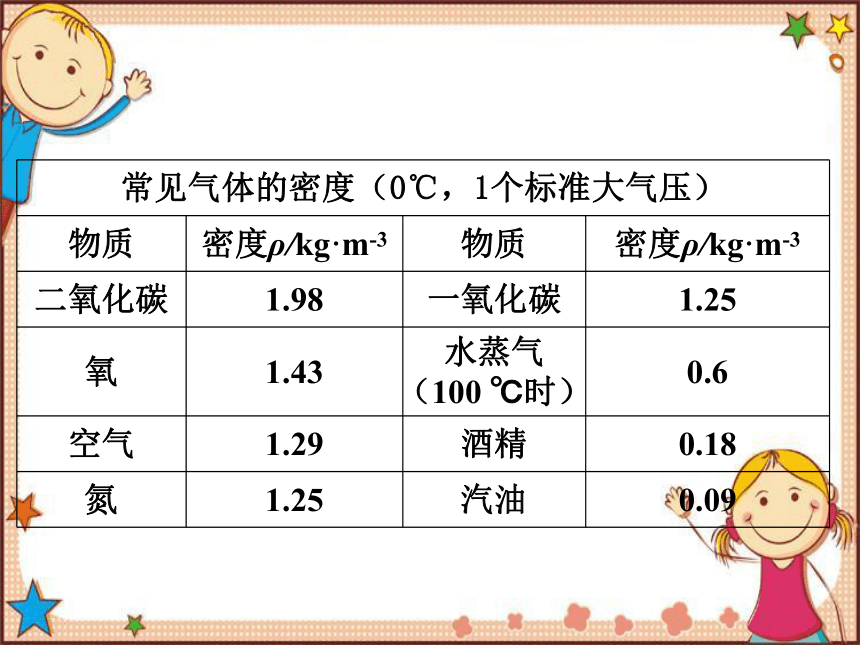
常见气体的密度(0℃,1个标准大气压)
物质 密度ρ/kg·m-3 物质 密度ρ/kg·m-3
二氧化碳 1.98 一氧化碳 1.25
氧 1.43 水蒸气(100 ℃时) 0.6
空气 1.29 酒精 0.18
氮 1.25 汽油 0.09
1.密度表列出了一些物质的密度,根据密度表能查找某种物质的_______,根据密度的大小能判定是哪一种_______.
2.由密度表发现的信息:每种物质都有自己的密度,物质不同,密度一般______;有的物质不同,但密度却______,如煤油和酒精;物质的密度会随物质______的变化而变化.
密度
物质
不同
相同
状态
3.密度的公式是_______,密度公式的变形公式有________和_______.
4.密度知识的运用:
(1)鉴别物质:测出物体的质量和体积,求出其_____,对照密度表就可判断物质种类.
密度
(2)估测物体的体积:知道物体的质量m,查出密度ρ,用_______可求出物体体积.
(3)估测物体的质量:测出体积,查出密度ρ,用_______可求物体质量.
例题讲解:
例题1 小明同学代表学校参加全市乒乓球比赛,获得了一枚金牌.他想知道该金牌是否是纯金的,于是利用实验室里的器材测出该金牌的质量为44.5 g,体积为5 cm3.你能利用这些数据帮助他作出判断吗?
解:(1)奖牌的密度:
查表可知,该奖牌可能是由铜制成的.
例题2 测得一长方形薄铝板的长为5 m,宽为1 m,测得其质量为13.5 kg,从密度表上查得铝的密度为2.7×103 kg/m3,这块铝板的厚度是多少?
解:铝板的体积:
铝板的底面积:S=5 m×1 m=5 m2
铝板的厚度:
课堂练习:
1.用密度为2.7×103 kg/m3的铝制成甲、乙、
丙三个大小不同的正方体,要求它们的边
长分别是0.1 m、0.2 m和0.3 m,制成后让
质量检查员称出它们的质量,分别是3 kg、
21.6 kg和54 kg,质量检查员指出,有两个
不合格,其中一个掺入了杂质为次品,另一
个混入了空气泡为废品,则这三个正方体
( )
A.甲为废品,乙为合格品,丙为次品
B.甲为合格品,乙为废品,丙为次品
C.甲为次品,乙为合格品,丙为废品
D.甲为废品,乙为次品,丙为合格品
C
解析:甲的体积:V甲=0.1 m×0.1 m×0.1 m
=0.001 m3,则甲的密度:
乙的体积:V乙=0.2 m×0.2 m×0.2 m=0.008 m3,则乙的密度:
丙的体积:V丙=0.3 m×0.3 m×0.3 m=0.027 m3,
则丙的密度:
因为ρ乙=ρ铝,所以乙是合格品;因为ρ丙<ρ铝,所以丙是废品;因为ρ甲>ρ铝,所以甲是次品.
2. 甲、乙、丙三个正方体,边长之比为1:2:3,质量分别为3 g、24 g、36 g,已知它们是同一材料制成的,但有一个是空心的,则空心的正方体是 ( )
A.甲 B.乙
C.丙 D.无法判断
C
解析:甲、乙、丙三个正方体的边长分别为1 cm,2 cm,3 cm.则它们的体积分别为:
V甲=(1 cm)3=1 cm3,V乙=(2 cm)3=8 cm3,V丙=(3 cm)3=27 cm3,它们的密度分别为:
丙的密度小,所以可以肯定丙是空心的.
3. 一个空瓶子的质量是150 g,当装满水时,瓶和水的总质量是400 g;当装满另一种液体时,瓶和液体的总质量是350 g. 则这个瓶子的容积是______cm3,液体的密度是______
kg/m3.
250
800
解析:装满水时水的质量为m水=m瓶+水 -m瓶=400 g-150 g=250 g,瓶子的容积 :
装满液体时液体的质量为m液=m瓶+液 - m瓶=350 g-150g=200g,液体的密度:
谢 谢
第5章 质量与密度
第4节 密度知识的应用
关于密度,你有哪些了解
密度是物质的一种特性,不同物质的密度一般不同,知道了物质的密度就能确认是哪种物质了.
常见物质的密度
常见固体的密度
物质 密度ρ/kg·m-3 物质 密度ρ/kg·m-3
铂 21.5×103 花岗岩 (2.6~2.8)×103
金 19.3×103 玻璃 (2.4~2.8)×103
铅 11.3×103 混凝土 2.2×103
银 10.5×103 砖 (1.4~2.2)×103
铜 8.9×103 冰 0.9×103
钢、铁 7.9×103 石蜡 0.9×103
铝 2.7×103 干松木 0.5×103
常见液体的密度
物质 密度ρ/kg·m-3 物质 密度ρ/kg·m-3
汞 13.6×103 柴油 0.85×103
硫酸 1.8×103 煤油 0.8×103
海水 1.03×103 酒精 0.8×103
纯水 1.0×103 汽油 0.71×103
常见气体的密度(0℃,1个标准大气压)
物质 密度ρ/kg·m-3 物质 密度ρ/kg·m-3
二氧化碳 1.98 一氧化碳 1.25
氧 1.43 水蒸气(100 ℃时) 0.6
空气 1.29 酒精 0.18
氮 1.25 汽油 0.09
1.密度表列出了一些物质的密度,根据密度表能查找某种物质的_______,根据密度的大小能判定是哪一种_______.
2.由密度表发现的信息:每种物质都有自己的密度,物质不同,密度一般______;有的物质不同,但密度却______,如煤油和酒精;物质的密度会随物质______的变化而变化.
密度
物质
不同
相同
状态
3.密度的公式是_______,密度公式的变形公式有________和_______.
4.密度知识的运用:
(1)鉴别物质:测出物体的质量和体积,求出其_____,对照密度表就可判断物质种类.
密度
(2)估测物体的体积:知道物体的质量m,查出密度ρ,用_______可求出物体体积.
(3)估测物体的质量:测出体积,查出密度ρ,用_______可求物体质量.
例题讲解:
例题1 小明同学代表学校参加全市乒乓球比赛,获得了一枚金牌.他想知道该金牌是否是纯金的,于是利用实验室里的器材测出该金牌的质量为44.5 g,体积为5 cm3.你能利用这些数据帮助他作出判断吗?
解:(1)奖牌的密度:
查表可知,该奖牌可能是由铜制成的.
例题2 测得一长方形薄铝板的长为5 m,宽为1 m,测得其质量为13.5 kg,从密度表上查得铝的密度为2.7×103 kg/m3,这块铝板的厚度是多少?
解:铝板的体积:
铝板的底面积:S=5 m×1 m=5 m2
铝板的厚度:
课堂练习:
1.用密度为2.7×103 kg/m3的铝制成甲、乙、
丙三个大小不同的正方体,要求它们的边
长分别是0.1 m、0.2 m和0.3 m,制成后让
质量检查员称出它们的质量,分别是3 kg、
21.6 kg和54 kg,质量检查员指出,有两个
不合格,其中一个掺入了杂质为次品,另一
个混入了空气泡为废品,则这三个正方体
( )
A.甲为废品,乙为合格品,丙为次品
B.甲为合格品,乙为废品,丙为次品
C.甲为次品,乙为合格品,丙为废品
D.甲为废品,乙为次品,丙为合格品
C
解析:甲的体积:V甲=0.1 m×0.1 m×0.1 m
=0.001 m3,则甲的密度:
乙的体积:V乙=0.2 m×0.2 m×0.2 m=0.008 m3,则乙的密度:
丙的体积:V丙=0.3 m×0.3 m×0.3 m=0.027 m3,
则丙的密度:
因为ρ乙=ρ铝,所以乙是合格品;因为ρ丙<ρ铝,所以丙是废品;因为ρ甲>ρ铝,所以甲是次品.
2. 甲、乙、丙三个正方体,边长之比为1:2:3,质量分别为3 g、24 g、36 g,已知它们是同一材料制成的,但有一个是空心的,则空心的正方体是 ( )
A.甲 B.乙
C.丙 D.无法判断
C
解析:甲、乙、丙三个正方体的边长分别为1 cm,2 cm,3 cm.则它们的体积分别为:
V甲=(1 cm)3=1 cm3,V乙=(2 cm)3=8 cm3,V丙=(3 cm)3=27 cm3,它们的密度分别为:
丙的密度小,所以可以肯定丙是空心的.
3. 一个空瓶子的质量是150 g,当装满水时,瓶和水的总质量是400 g;当装满另一种液体时,瓶和液体的总质量是350 g. 则这个瓶子的容积是______cm3,液体的密度是______
kg/m3.
250
800
解析:装满水时水的质量为m水=m瓶+水 -m瓶=400 g-150 g=250 g,瓶子的容积 :
装满液体时液体的质量为m液=m瓶+液 - m瓶=350 g-150g=200g,液体的密度:
谢 谢
同课章节目录
- 第一章 打开物理世界的大门
- 第一节 走进神奇
- 第二节 探索之路
- 第三节 站在巨人的肩膀上
- 第二章 运动的世界
- 第一节 动与静
- 第二节 长度与时间的测量
- 第三节 快与慢
- 第四节 科学探究:速度的变化
- 第三章 声的世界
- 第一节 科学探究:声音的产生与传播
- 第二节 声音的特性
- 第三节 超声与次声
- 第四章 多彩的光
- 第一节 光的反射
- 第二节 平面镜成像
- 第三节 光的折射
- 第四节 光的色散
- 第五节 科学探究:凸透镜成像
- 第六节 神奇的眼睛
- 第五章 质量与密度
- 第一节 质量
- 第二节 学习使用天平和量筒
- 第三节 科学探究:物质的密度
- 第四节 密度知识的应用
- 第六章 熟悉而陌生的力
- 第一节 力
- 第二节 怎样描述力
- 第三节 弹力与弹簧测力计
- 第四节 来自地球的力
- 第五节 科学探究:摩擦力
- 第七章 力与运动
- 第一节 科学探究:牛顿第一定律
- 第二节 力的合成
- 第三节 力的平衡
- 第八章 压强
- 第一节 压力的作用效果
- 第二节 科学探究:液体的压强
- 第三节 空气的“力量”
- 第四节 流体压强与流速的关系
- 第九章 浮力
- 第一节 认识浮力
- 第二节 阿基米德原理
- 第三节 物体的浮与沉
- 第十章 机械与人
- 第一节 科学探究:杠杆的平衡条件
- 第二节 滑轮及其应用
- 第三节 做功了吗
- 第四节 做功的快慢
- 第五节 机械效率
- 第六节 合理利用机械能
- 第十一章 小粒子与大宇宙
- 第一节 走进微观
- 第二节 看不见的运动
- 第三节 探索宇宙
