冀教版数学七年级下册 10.2不等式的基本性质课件(共18张PPT)
文档属性
| 名称 | 冀教版数学七年级下册 10.2不等式的基本性质课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-04 22:15:54 | ||
图片预览






文档简介
(共18张PPT)
10.2 不等式的性质
100g
50g
情境引入
天平不是永远平衡,人生的天平也总是倾斜于努力多的这一边。如果用砝码大小衡量一个人努力程度,每努力一次加3g砝码,现在小强努力程度是50g,他要多少次努力才超过100g?
设努力的次数为
怎么解这个不等式呢?
学习目标
1.通过观察、类比和归纳,探究不等式的基本性质,体会不等式变形和等式变形的区别和联系。
2.掌握不等式的基本性质并能熟练应用不等式的基本性质进行不等式的变形。
导入新课
一、温故而探新
如果a=b,那么
等式基本性质1:在等式的两边都加上(或减去)同一个数或整式,所得的结果仍是等式.
等式基本性质2:在等式的两边都乘以或除以同一个数(除数不为0),所得的结果仍是等式.
=
=
=
=
学生活动:请同学们观察——类比------猜想不等式的基本性质
并仿照等式基本性质写出来。
b
a
数轴的单位长度
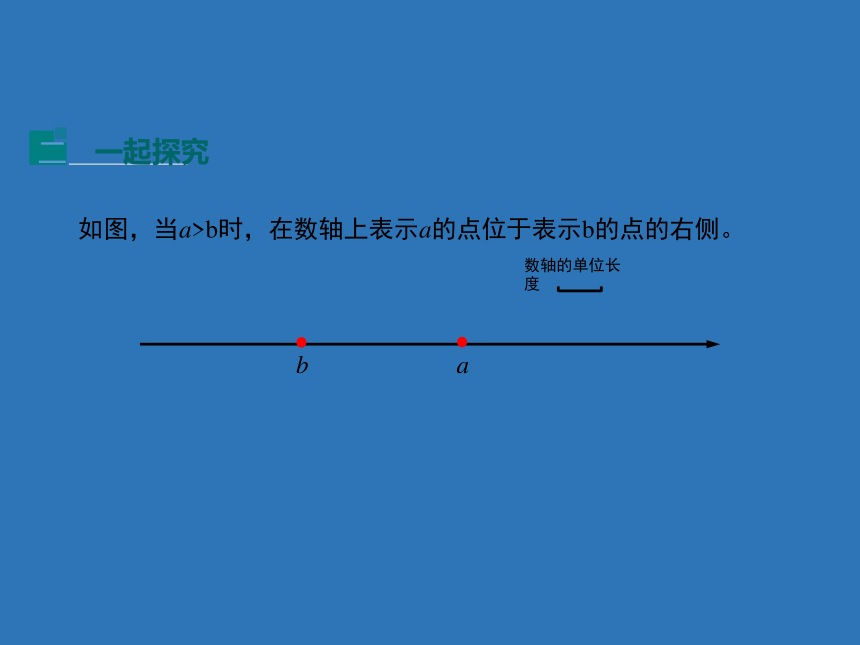
如图,当a>b时,在数轴上表示a的点位于表示b的点的右侧。
一起探究
二
b
a
数轴的单位长度
在数轴上,与a+3,b+3 对应的点和与a,b 对应的点之间具有如下的位置关系:
一起探究
二
b+3
b对应的点向右平移3个单位长度
a对应的点向右平移3个单位长度
a+3
思考并回答:
问题:1、a、b两点都向右移动5个单位,都向左移动5个单位呢?
2、a、b两点都向右移动c个单位呢?c是正数
3、a、b两点都向左移动c个单位呢?c是正数
计算并填空:
(1) 5>3, 5+2___3+2 , 5-2___3-2 ;
(2) -1<3, -1+2___3+2 , -1-3___3-3 .
根据发现的规律填空:当不等式两边加或减同一个数(正数
或负数)时,不等号的方向______.
不变
>
>
<
<
不等式的基本性质
一
讲授新课
探究成果1
不等式具有如下性质:不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.即
不等式基本性质1 :
如果a>b,那么 a ± c > b ± c.
讲授新课
不等式的基本性质
一
问题 水果店的小王从水果批发市场购进100kg梨和84kg苹果. 在卖出a kg梨和a kg苹果后,又分别各购进了b kg的梨和苹果.
100 -a 84 -a
>
请用“>”或“<”填空:
100 > 84
100 –a+b 84 –a+b
>
问题2 已知苹果的价格是a元/kg,梨的价格是b元/kg,且a > b. 小李各买了3kg苹果和梨,则买哪种水果花钱较多?
用不等号填空: 3a 3b.
问题3 在某次知识抢答赛中,甲、乙两队的总得分分别为a,b,其中a>b. 已知每队人员均为3名,则哪队的平均得分高?
用不等号填空:
a÷3 b÷3.
>
>
从日常生活中感受不等式新的性质
同学们回答问题,你们发现了什么规律?
我想探究和交流:
8×2 3×2
8×(-2) 3×(-2)
8×0.5 3×0.5
8×(-0.5) 3×(-0.5)
8 ×0.01 3×0.01
8×(-0.01) 3×(-0.01)
已知8 > 3 ,计算并用不等号填空
把你的发现规律说出来,与大家一起分享
>
>
>
不等式还有如下性质:不等式的两边都乘(或除以)同一个正数,不等号的方向不变.即
探究成果2和3
不等式基本性质2 如果a > b,c > 0,那么 ac > bc.
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.即
不等式基本性质3 如果a > b,c < 0,那么 ac < bc .
同桌的甲、乙两名同学,争论着一个问题:甲同学说:
“5a>4a.” 乙同学说:“不确定” 请你评说一下两
名同学的观点究竟哪个正确?为什么?
辩一辩更清楚 我能说会道
提示:注意a的取值范围
设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
(1) a- 3____b - 3;
(2) a÷3____b÷3
(3) 0.1a____0.1b;
(4) -4a____-4b;
(5) 2a+3____2b+3;
(6)(m2+1)a____ (m2+1)b(m为常数)
>
>
>
>
>
<
不等式的性质1
不等式的性质2
不等式的性质2
不等式的性质3
不等式的性质1,2
不等式的性质2
我会用
将不等式化成“x>a”或“x<a”的形式
二
例2 将下列不等式化成“x>a”或“x照准目标 我会变
(1) x-1>2;
(2) 2x<x+2;
(4) -5x>20.
(3) ;
(1)x -1+1>2+1
x>3
(2)2x-xx<2
(3) x < 12
(4) x < -4
我会用
<
<
<
>
x<-5
x>1
x>-8
x>1/2
课堂小结
不等式的基本性质
不等式的基本性质1
不等式的基本性质2
不等式的基本性质3
如果a>b,那么 a ± c > b ± c.
如果a > b,c > 0,那么 ac > bc.
如果a > b,c < 0,那么 ac < bc .
应用
跟着老师一起背诵!
10.2 不等式的性质
100g
50g
情境引入
天平不是永远平衡,人生的天平也总是倾斜于努力多的这一边。如果用砝码大小衡量一个人努力程度,每努力一次加3g砝码,现在小强努力程度是50g,他要多少次努力才超过100g?
设努力的次数为
怎么解这个不等式呢?
学习目标
1.通过观察、类比和归纳,探究不等式的基本性质,体会不等式变形和等式变形的区别和联系。
2.掌握不等式的基本性质并能熟练应用不等式的基本性质进行不等式的变形。
导入新课
一、温故而探新
如果a=b,那么
等式基本性质1:在等式的两边都加上(或减去)同一个数或整式,所得的结果仍是等式.
等式基本性质2:在等式的两边都乘以或除以同一个数(除数不为0),所得的结果仍是等式.
=
=
=
=
学生活动:请同学们观察——类比------猜想不等式的基本性质
并仿照等式基本性质写出来。
b
a
数轴的单位长度
如图,当a>b时,在数轴上表示a的点位于表示b的点的右侧。
一起探究
二
b
a
数轴的单位长度
在数轴上,与a+3,b+3 对应的点和与a,b 对应的点之间具有如下的位置关系:
一起探究
二
b+3
b对应的点向右平移3个单位长度
a对应的点向右平移3个单位长度
a+3
思考并回答:
问题:1、a、b两点都向右移动5个单位,都向左移动5个单位呢?
2、a、b两点都向右移动c个单位呢?c是正数
3、a、b两点都向左移动c个单位呢?c是正数
计算并填空:
(1) 5>3, 5+2___3+2 , 5-2___3-2 ;
(2) -1<3, -1+2___3+2 , -1-3___3-3 .
根据发现的规律填空:当不等式两边加或减同一个数(正数
或负数)时,不等号的方向______.
不变
>
>
<
<
不等式的基本性质
一
讲授新课
探究成果1
不等式具有如下性质:不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.即
不等式基本性质1 :
如果a>b,那么 a ± c > b ± c.
讲授新课
不等式的基本性质
一
问题 水果店的小王从水果批发市场购进100kg梨和84kg苹果. 在卖出a kg梨和a kg苹果后,又分别各购进了b kg的梨和苹果.
100 -a 84 -a
>
请用“>”或“<”填空:
100 > 84
100 –a+b 84 –a+b
>
问题2 已知苹果的价格是a元/kg,梨的价格是b元/kg,且a > b. 小李各买了3kg苹果和梨,则买哪种水果花钱较多?
用不等号填空: 3a 3b.
问题3 在某次知识抢答赛中,甲、乙两队的总得分分别为a,b,其中a>b. 已知每队人员均为3名,则哪队的平均得分高?
用不等号填空:
a÷3 b÷3.
>
>
从日常生活中感受不等式新的性质
同学们回答问题,你们发现了什么规律?
我想探究和交流:
8×2 3×2
8×(-2) 3×(-2)
8×0.5 3×0.5
8×(-0.5) 3×(-0.5)
8 ×0.01 3×0.01
8×(-0.01) 3×(-0.01)
已知8 > 3 ,计算并用不等号填空
把你的发现规律说出来,与大家一起分享
>
>
>
不等式还有如下性质:不等式的两边都乘(或除以)同一个正数,不等号的方向不变.即
探究成果2和3
不等式基本性质2 如果a > b,c > 0,那么 ac > bc.
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.即
不等式基本性质3 如果a > b,c < 0,那么 ac < bc .
同桌的甲、乙两名同学,争论着一个问题:甲同学说:
“5a>4a.” 乙同学说:“不确定” 请你评说一下两
名同学的观点究竟哪个正确?为什么?
辩一辩更清楚 我能说会道
提示:注意a的取值范围
设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
(1) a- 3____b - 3;
(2) a÷3____b÷3
(3) 0.1a____0.1b;
(4) -4a____-4b;
(5) 2a+3____2b+3;
(6)(m2+1)a____ (m2+1)b(m为常数)
>
>
>
>
>
<
不等式的性质1
不等式的性质2
不等式的性质2
不等式的性质3
不等式的性质1,2
不等式的性质2
我会用
将不等式化成“x>a”或“x<a”的形式
二
例2 将下列不等式化成“x>a”或“x
(1) x-1>2;
(2) 2x<x+2;
(4) -5x>20.
(3) ;
(1)x -1+1>2+1
x>3
(2)2x-x
(3) x < 12
(4) x < -4
我会用
<
<
<
>
x<-5
x>1
x>-8
x>1/2
课堂小结
不等式的基本性质
不等式的基本性质1
不等式的基本性质2
不等式的基本性质3
如果a>b,那么 a ± c > b ± c.
如果a > b,c > 0,那么 ac > bc.
如果a > b,c < 0,那么 ac < bc .
应用
跟着老师一起背诵!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
