7.3独立性检验问题
图片预览



文档简介
§3 独立性检验问题
3.1 独立性检验
3.2 独立性检验的基本思想
3.3 独立性检验的应用
最新课标 (1)通过实例,理解2×2列联表的统计意义. (2)通过实例,了解2×2列联表独立性检验及其应用.
[教材要点]
要点一 2×2列联表
设A,B为两个变量,每一个变量都可以取两个值,
变量A:A1,A2=;
变量B:B1,B2=.
则下表称为列联表:
AB B1 B2 总计
A1 a b a+b
A2 c d c+d
总计 a+c b+d n=a+b+c+d
状元随笔 (1)列联表是两个或两个以上分类变量的汇总统计表,现阶段我们仅研究两个分类变量的列联表,并且每个分类变量只取两个值,这样的列联表称为2×2列联表.
(2)列联表有助于直观地观测数据之间的关系,如a表示既满足x1,又满足y1的样本量,表示在x1情况下,又满足y1条件的样本所占的频率.
要点二 独立性检验的基本思想
1.定义:利用χ2的取值推断分类变量X和Y是否独立性的方法称为χ2独立性检验,读作“卡方独立性检验”,简称独立性检验.
2.公式:χ2=.
3.判断方法
(1)当χ2≤2.706时,没有充分的证据判断变量A,B有关联,可以认为变量A,B是没有关联的;
(2)当χ2>2.706时,有90%的把握判断变量A,B有关联;
(3)当χ2>3.841时,有95%的把握判断变量A,B有关联;
(4)当χ2>6.635时,有99%的把握判断变量A,B有关联.
状元随笔 列联表中的数据是样本数据,它只是总体的代表,具有随机性,因此,需要用独立性检验的方法确认所得结论在多大程度上适用于总体,即独立性检验得出的结论是带有概率性质的,只能说结论成立的概率有多大,而不能完全肯定一个结论,在分析问题时一定要注意这点,不可对某个问题下确定性结论,否则就可能对统计计算的结果做出错误的解释,比如:
χ2≥6.635,就认为有99%的把握认为“两个分类变量有关系”.
通常认为χ2≤2.706时,样本数据中没有充分的证据支持结论“两个分类变量有关系”.
[基础自测]
1.思考辨析(正确的画“√”,错误的画“×”)
(1)列联表中的数据是两个变量的频数.( )
(2)2×2列联表只有4个格子.( )
(3)χ2的大小是判断变量A与B是否相关的统计量.( )
2.对两个变量A与B的χ2的值说法正确的是( )
A.χ2越大,“A与B有关”的把握性越小
B.χ2越小,“A与B有关”的把握性越小
C.χ2越接近于0,“A与B无关”的把握性越小
D.χ2越大,“A与B无关”的把握性越大
3.如表是一个2×2列联表:则表中a,b的值分别为( )
y1 y2 合计
x1 a 21 73
x2 22 25 47
合计 b 46 120
A.94,72 B.52,50
C.52,74 D.74,52
4.在对人们休闲方式的一次调查中,根据数据建立如下的2×2列联表:
看书 运动 合计
男 8 20 28
女 16 12 28
合计 24 32 56
根据表中数据,得到χ2=≈4.667,所以我们至少有________的把握判定休闲方式与性别有关系.
题型一 对独立性检验思想的理解
例1 在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得:有99%的把握判断“吸烟与患肺癌有关”的结论,下列说法中正确的是( )
A.100个吸烟者中至少有99人患有肺癌
B.1个人吸烟,那么这个人有99%的概率患有肺癌
C.在100个吸烟者中一定有患肺癌的人
D.在100个吸烟者中可能一个患肺癌的人也没有
方法归纳
独立性检验的注意事项
(1)独立性检验的关键是正确列出2×2列联表,求出“合计”栏,然后正确求出χ2值.
(2)独立性检验中,如果两个分类变量之间有关系,则独立性检验是对两个变量有关系的可信程度的判断.
跟踪训练1 为考察某动物疫苗预防某种疾病的效果,现对200只动物进行调研,并得到如下数据:
未发病 发病 合计
未接种疫苗 20 60 80
接种疫苗 80 40 120
合计 100 100 200
则下列说法正确的是( )
A.至少有99%的把握认为“发病与未接种疫苗有关”
B.至多有99%的把握认为“发病与未接种疫苗有关”
C.至多有99%的把握认为“发病与未接种疫苗无关”
D.“发病与未接种疫苗有关”的错误率至少有0.01%
题型二 独立性检验的应用
例2 我校随机抽取100名学生,对其学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参与 班级工作 不太主动参 加班级工作 合计
学习积极性高 40
学习积极性一般 30
合计100
已知随机抽查这100名学生中的一名学生,抽到积极参加班级工作的学生的概率是0.6.
(1)请将上表补充完整(不用写计算过程).
(2)试问:学生的学习积极性是否与对待班级工作的态度有关?
方法归纳
用独立性检验求解实际问题的基本步骤
(1)认真读题,根据相关数据列出2×2列联表;
(2)计算:将2×2列联表中的数据代入公式求出χ2的值.
(3)判断:根据统计中的数据判断,得出结论.
跟踪训练2 某生产线上,质量监督员甲在生产现场时,990件产品中有合格品982件,次品8件;不在生产现场时,510件产品中有合格品493件,次品17件.是否有99%的把握认为质量监督员甲在不在生产现场与产品质量好坏有关系?
题型三 独立性检验的综合应用
例3 某校鼓励即将毕业的大学生到西部偏远地区去支教,校学生就业部针对即将毕业的男、女生是否愿意到西部支教进行问卷调查,得到的情况如下表所示:
性别 支教 合计
愿意去支教 不愿意去支教
女生 20
男生 40
合计 70 100
(1)完成上述2×2列联表.
(2)根据表中的数据,试问愿意去西部支教是否与性别有关?
(3)若在接受调查的所有男生中按照“是否愿意去支教”进行分层抽样,随机抽取10人,再在10人中抽取3人进行面谈,记面谈的男生中,不愿意去支教的人数为ξ,求ξ的分布列以及数学期望.
方法归纳
独立性检验经常与其他知识综合考查,如分布列、分层抽样、频率分布直方图、计数原理、线性回归方程、正态分布等.解决此类问题的关键是正确应用各个知识点,注意参考公式和数据.另外,此类题目一般为实际应用问题,要细细阅读理解,明确题目信息.
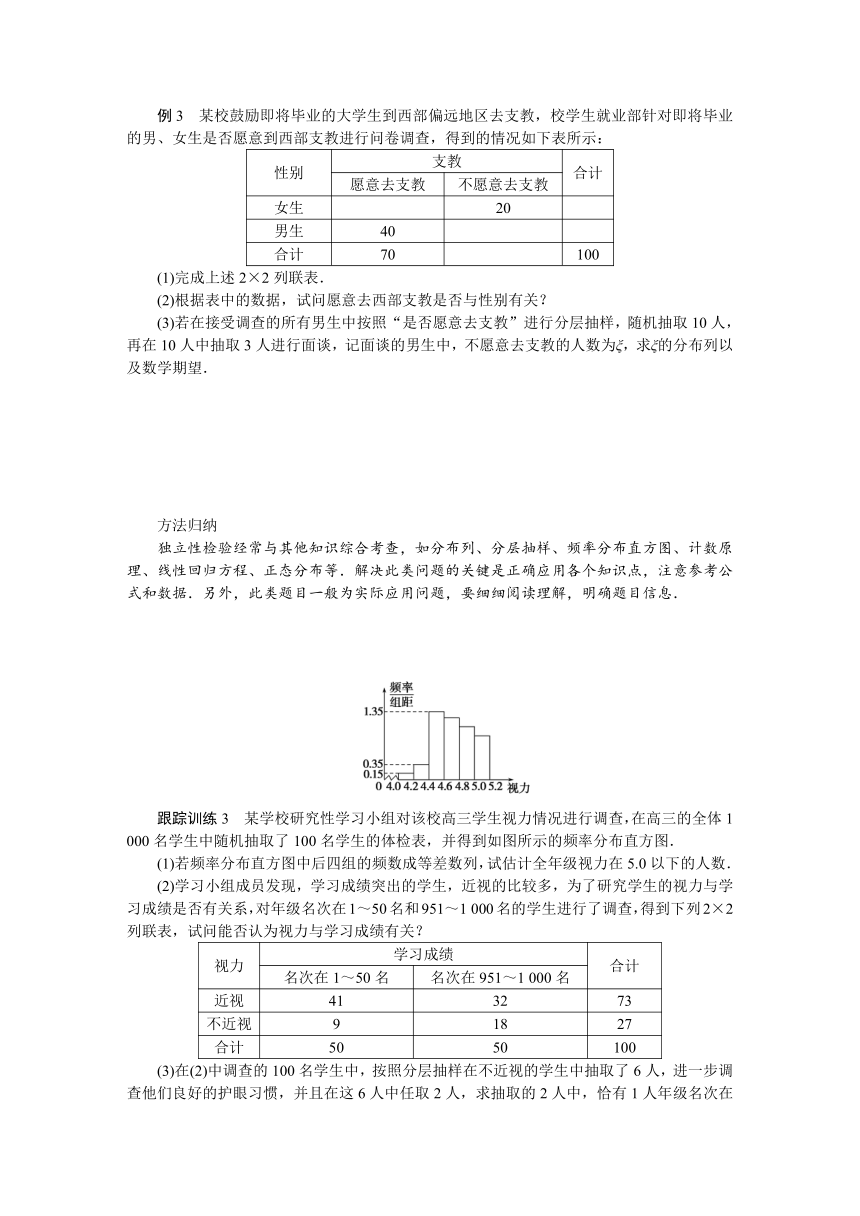
跟踪训练3 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1 000名学生中随机抽取了100名学生的体检表,并得到如图所示的频率分布直方图.
(1)若频率分布直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数.
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1 000名的学生进行了调查,得到下列2×2列联表,试问能否认为视力与学习成绩有关?
视力 学习成绩 合计
名次在1~50名 名次在951~1 000名
近视 41 32 73
不近视 9 18 27
合计 50 50 100
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了6人,进一步调查他们良好的护眼习惯,并且在这6人中任取2人,求抽取的2人中,恰有1人年级名次在1~50名的概率.
易错辨析 因不理解独立性检验的含义致误
例4 调查者通过询问男、女大学生在购买食品时是否看生产日期和保质期得到的数据如下表所示,试分析看生产日期和保质期是否与性别有关.
看生产日期和保质期 不看生产日期和保质期 合计
男大学生 23 32 55
女大学生 9 25 34
合计 32 57 89
解析:由题意,χ2=≈2.149<2.706.
所以没有发现足够的证据说明看生产日期和保质期与性别有关.
【易错警示】
易错原因 纠错心得
有些学生会通过列联表计算出比大,因此认为看生产日期和保质期与性别有关. 实际上这只能说明二者有关成立的可能性比较大,即并不能肯定地说二者有关,若要判定看生产日期和保质期与性别有关,则需进行独立性检验. 列联表只能粗略地判断两个变量是否有关,独立性检验才能更精准地分析.但由独立性检验得出的结论也不是“一定”有关或无关.
[课堂十分钟]
1.在一项中学生近视情况的调查中,某校男生150名中有80名近视,女生140名中有70名近视,在检验这些中学生眼睛近视是否与性别有关时用什么方法最有说服力( )
A.平均数与方差 B.回归分析
C.独立性检验 D.概率
2.分类变量X和Y的列表如下,则下列说法判断正确的是( )
y1 y2 合计
x1 a b a+b
x2 c d c+d
合计 a+c b+d a+b+c+d
A.ad-bc越小,说明X和Y关系越弱
B.ad-bc越大,说明X和Y关系越强
C.(ad-bc)2越大,说明X与Y关系越强
D.(ad-bc)2越接近于0,说明X与Y关系越强
3.若由一个2×2列联表中的数据计算得χ2=4.013,那么有________把握认为两个变量有关.( )
A.95% B.97.5%
C.99% D.99.9%
4.下面2×2列联表的χ2的值为________.
B 合计
A 8 4 12
2 16 18
合计 10 20 30
5.在研究某种药物对“H7N9”病毒的治疗效果时,进行动物试验,得到以下数据,对150只动物服用药物,其中132只动物存活,18只动物死亡,对照组150只动物进行常规治疗,其中114只动物存活,36只动物死亡.
(1)根据以上数据建立一个2×2列联表.
(2)试问该种药物对治疗“H7N9”病毒是否有效?
§3 独立性检验问题
3.1 独立性检验
3.2 独立性检验的基本思想
3.3 独立性检验的应用
新知初探·课前预习
[基础自测]
1.(1)√ (2)× (3)√
2.解析:χ2越大,A与B越不独立,所以关联越大;相反,χ2越小,关联越小.故选B.
答案:B
3.解析:a=73-21=52,b=a+22=52+22=74.故选C.
答案:C
4.解析:根据表中数据得到χ2≈4.667>3.841,所以至少有95%的把握判定休闲方式与性别有关系.
答案:95%
题型探究·课堂解透
例1 解析:A.独立性检验的结论是一个数学统计量,它与实际问题中的问题的确定性是存在差异的,A错;B.χ2与概率的含义不同,有99%的把握认为结论正确不能说明有99%的可能患有肺癌,B错;C.独立性检验的结论是一个数学统计量,它与实际问题中的问题的确定性是存在差异的,C错;D.独立性检验的结论是一个数学统计量,它与实际问题中的问题的确定性是存在差异的,D正确.
答案:D
跟踪训练1 解析:χ2==>6.635
所以至少有99%的把握认为“发病与未接种疫苗有关”,故选A.
答案:A
例2 解析:(1)由题意,积极参加班级工作人数为100×0.6=60,列联表如下:
积极参与 班级工作 不太主动参加 班级工作 合计
学习积极性高 40 10 50
学习积极性一般 20 30 50
合计 60 40 100
(2)由公式计算得χ2=≈16.667>6.635
所以有99%的把握认为学习积极性与对待班级工作态度有关.
跟踪训练2 解析:根据题目所给数据得如下2×2列联表:
合格品 次品 合计
甲在生产现场 982 8 990
甲不在生产现场 493 17 510
合计 1 475 25 1 500
根据列联表中的数据,经计算得到
χ2=≈13.097>6.635.
所以有99%的把握认为质量监督员甲在不在生产现场与产品质量好坏有关.
例3 解析:(1)2×2列联表如下:
性别 支教 合计
愿意去支教 不愿意去支教
女生 30 20 50
男生 40 10 50
合计 70 30 100
(2)根据公式计算得χ2=≈4.762>3.841
所以有95%的把握认为是否愿意去西部支教与性别有关.
(3)由题意,抽取的10人中有8人愿意去西部支教,2人不愿意去西部支教,于是ξ=0,1,2,
∴P(ξ=0)==,P(ξ=1)==,
P(ξ=2)==.∴ξ的分布列为
ξ 0 1 2
P
∴E(ξ)=0×+1×+2×=.
跟踪训练3 解析:(1)由图可知第一组有3人,第二组有7人,第三组有27人.
因为后四组的频数成等差数列,且它们的和为90,公差小于0,
所以后四组的频数依次为27,24,21,18.
所以视力在5.0以下的人数为3+7+27+24+21=82(或者100-18=82),
故全年级视力在5.0以下的人数约为1 000×=820.
(2)由公式计算得χ2=≈4.110>3.841
所以有95%的把握认为视力与学习成绩有关.
(3)依题意得,6人中年级名次在1~50名的有2人,
年级名次在951~1 000名的有4人,
则从6人中任取2人的情况有
=8种,所以所求概率为.
[课堂十分钟]
1.解析:判断两个变量是否有关的最有效方法是进行独立性检验.
答案:C
2.解析:列联表可以较为准确地判断两个变量之间的相关关系程度,
由χ2=
当(ad-bc)2越大,χ2越大,表明X与Y的关系越强.
(ad-bc)2越接近0,说明两个分类变量X和Y无关的可能性越大.
答案:C
3.解析:∵χ2=4.013>3.841,∴有95%的把握认为两个变量有关.
答案:A
4.解析:χ2==10.
答案:10
5.解析:(1)2×2列联表如下:
存活数 死亡数 合计
服用药物 132 18 150
未服药物 114 36 150
合计 246 54 300
(2)由(1)知χ2=≈7.317>6.635.
故我们有99%的把握认为该种药物对“H7N9”病毒有治疗效果.
3.1 独立性检验
3.2 独立性检验的基本思想
3.3 独立性检验的应用
最新课标 (1)通过实例,理解2×2列联表的统计意义. (2)通过实例,了解2×2列联表独立性检验及其应用.
[教材要点]
要点一 2×2列联表
设A,B为两个变量,每一个变量都可以取两个值,
变量A:A1,A2=;
变量B:B1,B2=.
则下表称为列联表:
AB B1 B2 总计
A1 a b a+b
A2 c d c+d
总计 a+c b+d n=a+b+c+d
状元随笔 (1)列联表是两个或两个以上分类变量的汇总统计表,现阶段我们仅研究两个分类变量的列联表,并且每个分类变量只取两个值,这样的列联表称为2×2列联表.
(2)列联表有助于直观地观测数据之间的关系,如a表示既满足x1,又满足y1的样本量,表示在x1情况下,又满足y1条件的样本所占的频率.
要点二 独立性检验的基本思想
1.定义:利用χ2的取值推断分类变量X和Y是否独立性的方法称为χ2独立性检验,读作“卡方独立性检验”,简称独立性检验.
2.公式:χ2=.
3.判断方法
(1)当χ2≤2.706时,没有充分的证据判断变量A,B有关联,可以认为变量A,B是没有关联的;
(2)当χ2>2.706时,有90%的把握判断变量A,B有关联;
(3)当χ2>3.841时,有95%的把握判断变量A,B有关联;
(4)当χ2>6.635时,有99%的把握判断变量A,B有关联.
状元随笔 列联表中的数据是样本数据,它只是总体的代表,具有随机性,因此,需要用独立性检验的方法确认所得结论在多大程度上适用于总体,即独立性检验得出的结论是带有概率性质的,只能说结论成立的概率有多大,而不能完全肯定一个结论,在分析问题时一定要注意这点,不可对某个问题下确定性结论,否则就可能对统计计算的结果做出错误的解释,比如:
χ2≥6.635,就认为有99%的把握认为“两个分类变量有关系”.
通常认为χ2≤2.706时,样本数据中没有充分的证据支持结论“两个分类变量有关系”.
[基础自测]
1.思考辨析(正确的画“√”,错误的画“×”)
(1)列联表中的数据是两个变量的频数.( )
(2)2×2列联表只有4个格子.( )
(3)χ2的大小是判断变量A与B是否相关的统计量.( )
2.对两个变量A与B的χ2的值说法正确的是( )
A.χ2越大,“A与B有关”的把握性越小
B.χ2越小,“A与B有关”的把握性越小
C.χ2越接近于0,“A与B无关”的把握性越小
D.χ2越大,“A与B无关”的把握性越大
3.如表是一个2×2列联表:则表中a,b的值分别为( )
y1 y2 合计
x1 a 21 73
x2 22 25 47
合计 b 46 120
A.94,72 B.52,50
C.52,74 D.74,52
4.在对人们休闲方式的一次调查中,根据数据建立如下的2×2列联表:
看书 运动 合计
男 8 20 28
女 16 12 28
合计 24 32 56
根据表中数据,得到χ2=≈4.667,所以我们至少有________的把握判定休闲方式与性别有关系.
题型一 对独立性检验思想的理解
例1 在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得:有99%的把握判断“吸烟与患肺癌有关”的结论,下列说法中正确的是( )
A.100个吸烟者中至少有99人患有肺癌
B.1个人吸烟,那么这个人有99%的概率患有肺癌
C.在100个吸烟者中一定有患肺癌的人
D.在100个吸烟者中可能一个患肺癌的人也没有
方法归纳
独立性检验的注意事项
(1)独立性检验的关键是正确列出2×2列联表,求出“合计”栏,然后正确求出χ2值.
(2)独立性检验中,如果两个分类变量之间有关系,则独立性检验是对两个变量有关系的可信程度的判断.
跟踪训练1 为考察某动物疫苗预防某种疾病的效果,现对200只动物进行调研,并得到如下数据:
未发病 发病 合计
未接种疫苗 20 60 80
接种疫苗 80 40 120
合计 100 100 200
则下列说法正确的是( )
A.至少有99%的把握认为“发病与未接种疫苗有关”
B.至多有99%的把握认为“发病与未接种疫苗有关”
C.至多有99%的把握认为“发病与未接种疫苗无关”
D.“发病与未接种疫苗有关”的错误率至少有0.01%
题型二 独立性检验的应用
例2 我校随机抽取100名学生,对其学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参与 班级工作 不太主动参 加班级工作 合计
学习积极性高 40
学习积极性一般 30
合计100
已知随机抽查这100名学生中的一名学生,抽到积极参加班级工作的学生的概率是0.6.
(1)请将上表补充完整(不用写计算过程).
(2)试问:学生的学习积极性是否与对待班级工作的态度有关?
方法归纳
用独立性检验求解实际问题的基本步骤
(1)认真读题,根据相关数据列出2×2列联表;
(2)计算:将2×2列联表中的数据代入公式求出χ2的值.
(3)判断:根据统计中的数据判断,得出结论.
跟踪训练2 某生产线上,质量监督员甲在生产现场时,990件产品中有合格品982件,次品8件;不在生产现场时,510件产品中有合格品493件,次品17件.是否有99%的把握认为质量监督员甲在不在生产现场与产品质量好坏有关系?
题型三 独立性检验的综合应用
例3 某校鼓励即将毕业的大学生到西部偏远地区去支教,校学生就业部针对即将毕业的男、女生是否愿意到西部支教进行问卷调查,得到的情况如下表所示:
性别 支教 合计
愿意去支教 不愿意去支教
女生 20
男生 40
合计 70 100
(1)完成上述2×2列联表.
(2)根据表中的数据,试问愿意去西部支教是否与性别有关?
(3)若在接受调查的所有男生中按照“是否愿意去支教”进行分层抽样,随机抽取10人,再在10人中抽取3人进行面谈,记面谈的男生中,不愿意去支教的人数为ξ,求ξ的分布列以及数学期望.
方法归纳
独立性检验经常与其他知识综合考查,如分布列、分层抽样、频率分布直方图、计数原理、线性回归方程、正态分布等.解决此类问题的关键是正确应用各个知识点,注意参考公式和数据.另外,此类题目一般为实际应用问题,要细细阅读理解,明确题目信息.
跟踪训练3 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1 000名学生中随机抽取了100名学生的体检表,并得到如图所示的频率分布直方图.
(1)若频率分布直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数.
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1 000名的学生进行了调查,得到下列2×2列联表,试问能否认为视力与学习成绩有关?
视力 学习成绩 合计
名次在1~50名 名次在951~1 000名
近视 41 32 73
不近视 9 18 27
合计 50 50 100
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了6人,进一步调查他们良好的护眼习惯,并且在这6人中任取2人,求抽取的2人中,恰有1人年级名次在1~50名的概率.
易错辨析 因不理解独立性检验的含义致误
例4 调查者通过询问男、女大学生在购买食品时是否看生产日期和保质期得到的数据如下表所示,试分析看生产日期和保质期是否与性别有关.
看生产日期和保质期 不看生产日期和保质期 合计
男大学生 23 32 55
女大学生 9 25 34
合计 32 57 89
解析:由题意,χ2=≈2.149<2.706.
所以没有发现足够的证据说明看生产日期和保质期与性别有关.
【易错警示】
易错原因 纠错心得
有些学生会通过列联表计算出比大,因此认为看生产日期和保质期与性别有关. 实际上这只能说明二者有关成立的可能性比较大,即并不能肯定地说二者有关,若要判定看生产日期和保质期与性别有关,则需进行独立性检验. 列联表只能粗略地判断两个变量是否有关,独立性检验才能更精准地分析.但由独立性检验得出的结论也不是“一定”有关或无关.
[课堂十分钟]
1.在一项中学生近视情况的调查中,某校男生150名中有80名近视,女生140名中有70名近视,在检验这些中学生眼睛近视是否与性别有关时用什么方法最有说服力( )
A.平均数与方差 B.回归分析
C.独立性检验 D.概率
2.分类变量X和Y的列表如下,则下列说法判断正确的是( )
y1 y2 合计
x1 a b a+b
x2 c d c+d
合计 a+c b+d a+b+c+d
A.ad-bc越小,说明X和Y关系越弱
B.ad-bc越大,说明X和Y关系越强
C.(ad-bc)2越大,说明X与Y关系越强
D.(ad-bc)2越接近于0,说明X与Y关系越强
3.若由一个2×2列联表中的数据计算得χ2=4.013,那么有________把握认为两个变量有关.( )
A.95% B.97.5%
C.99% D.99.9%
4.下面2×2列联表的χ2的值为________.
B 合计
A 8 4 12
2 16 18
合计 10 20 30
5.在研究某种药物对“H7N9”病毒的治疗效果时,进行动物试验,得到以下数据,对150只动物服用药物,其中132只动物存活,18只动物死亡,对照组150只动物进行常规治疗,其中114只动物存活,36只动物死亡.
(1)根据以上数据建立一个2×2列联表.
(2)试问该种药物对治疗“H7N9”病毒是否有效?
§3 独立性检验问题
3.1 独立性检验
3.2 独立性检验的基本思想
3.3 独立性检验的应用
新知初探·课前预习
[基础自测]
1.(1)√ (2)× (3)√
2.解析:χ2越大,A与B越不独立,所以关联越大;相反,χ2越小,关联越小.故选B.
答案:B
3.解析:a=73-21=52,b=a+22=52+22=74.故选C.
答案:C
4.解析:根据表中数据得到χ2≈4.667>3.841,所以至少有95%的把握判定休闲方式与性别有关系.
答案:95%
题型探究·课堂解透
例1 解析:A.独立性检验的结论是一个数学统计量,它与实际问题中的问题的确定性是存在差异的,A错;B.χ2与概率的含义不同,有99%的把握认为结论正确不能说明有99%的可能患有肺癌,B错;C.独立性检验的结论是一个数学统计量,它与实际问题中的问题的确定性是存在差异的,C错;D.独立性检验的结论是一个数学统计量,它与实际问题中的问题的确定性是存在差异的,D正确.
答案:D
跟踪训练1 解析:χ2==>6.635
所以至少有99%的把握认为“发病与未接种疫苗有关”,故选A.
答案:A
例2 解析:(1)由题意,积极参加班级工作人数为100×0.6=60,列联表如下:
积极参与 班级工作 不太主动参加 班级工作 合计
学习积极性高 40 10 50
学习积极性一般 20 30 50
合计 60 40 100
(2)由公式计算得χ2=≈16.667>6.635
所以有99%的把握认为学习积极性与对待班级工作态度有关.
跟踪训练2 解析:根据题目所给数据得如下2×2列联表:
合格品 次品 合计
甲在生产现场 982 8 990
甲不在生产现场 493 17 510
合计 1 475 25 1 500
根据列联表中的数据,经计算得到
χ2=≈13.097>6.635.
所以有99%的把握认为质量监督员甲在不在生产现场与产品质量好坏有关.
例3 解析:(1)2×2列联表如下:
性别 支教 合计
愿意去支教 不愿意去支教
女生 30 20 50
男生 40 10 50
合计 70 30 100
(2)根据公式计算得χ2=≈4.762>3.841
所以有95%的把握认为是否愿意去西部支教与性别有关.
(3)由题意,抽取的10人中有8人愿意去西部支教,2人不愿意去西部支教,于是ξ=0,1,2,
∴P(ξ=0)==,P(ξ=1)==,
P(ξ=2)==.∴ξ的分布列为
ξ 0 1 2
P
∴E(ξ)=0×+1×+2×=.
跟踪训练3 解析:(1)由图可知第一组有3人,第二组有7人,第三组有27人.
因为后四组的频数成等差数列,且它们的和为90,公差小于0,
所以后四组的频数依次为27,24,21,18.
所以视力在5.0以下的人数为3+7+27+24+21=82(或者100-18=82),
故全年级视力在5.0以下的人数约为1 000×=820.
(2)由公式计算得χ2=≈4.110>3.841
所以有95%的把握认为视力与学习成绩有关.
(3)依题意得,6人中年级名次在1~50名的有2人,
年级名次在951~1 000名的有4人,
则从6人中任取2人的情况有
=8种,所以所求概率为.
[课堂十分钟]
1.解析:判断两个变量是否有关的最有效方法是进行独立性检验.
答案:C
2.解析:列联表可以较为准确地判断两个变量之间的相关关系程度,
由χ2=
当(ad-bc)2越大,χ2越大,表明X与Y的关系越强.
(ad-bc)2越接近0,说明两个分类变量X和Y无关的可能性越大.
答案:C
3.解析:∵χ2=4.013>3.841,∴有95%的把握认为两个变量有关.
答案:A
4.解析:χ2==10.
答案:10
5.解析:(1)2×2列联表如下:
存活数 死亡数 合计
服用药物 132 18 150
未服药物 114 36 150
合计 246 54 300
(2)由(1)知χ2=≈7.317>6.635.
故我们有99%的把握认为该种药物对“H7N9”病毒有治疗效果.
同课章节目录
