第二章 圆锥曲线 章末复习课 学案(Word版含答案)
文档属性
| 名称 | 第二章 圆锥曲线 章末复习课 学案(Word版含答案) | 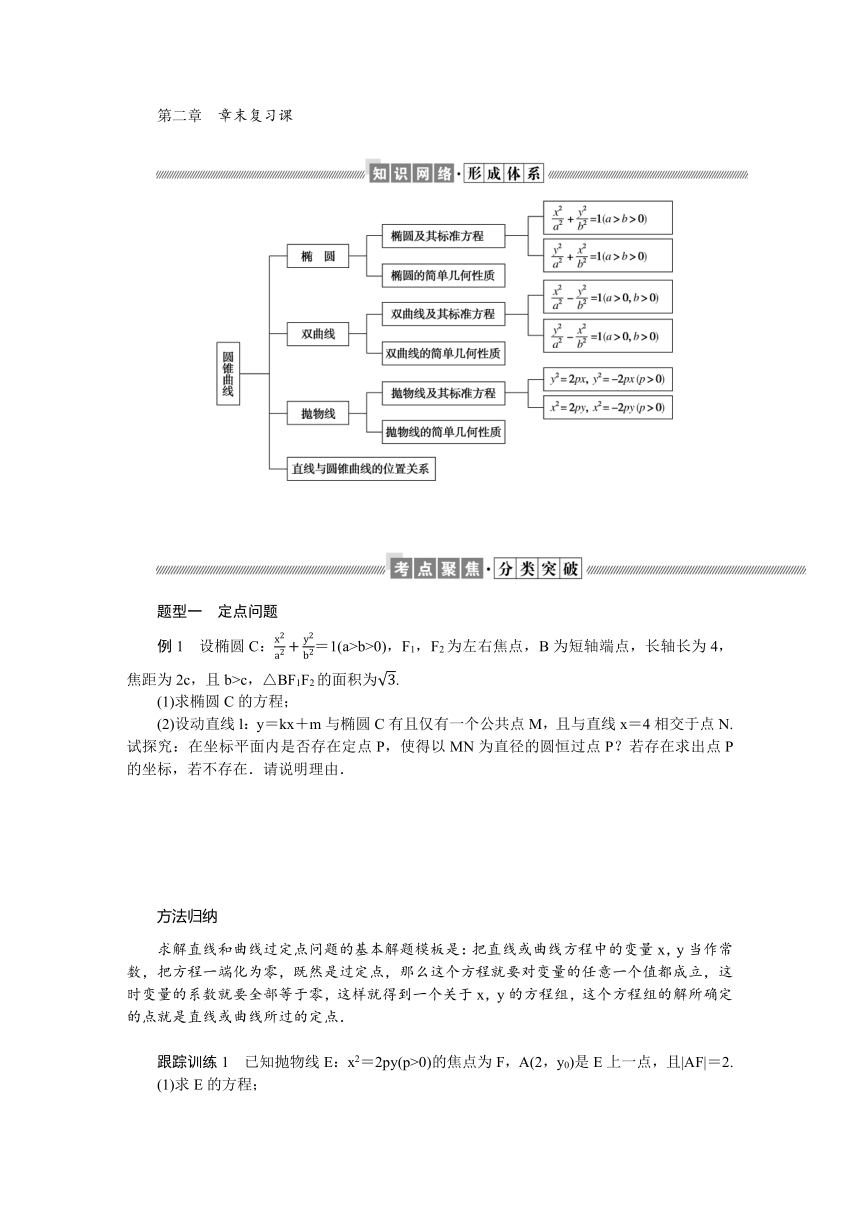 | |
| 格式 | docx | ||
| 文件大小 | 215.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-04 23:29:38 | ||
图片预览




文档简介
第二章 章末复习课
题型一 定点问题
例1 设椭圆C:=1(a>b>0),F1,F2为左右焦点,B为短轴端点,长轴长为4,焦距为2c,且b>c,△BF1F2的面积为.
(1)求椭圆C的方程;
(2)设动直线l:y=kx+m与椭圆C有且仅有一个公共点M,且与直线x=4相交于点N.试探究:在坐标平面内是否存在定点P,使得以MN为直径的圆恒过点P?若存在求出点P的坐标,若不存在.请说明理由.
方法归纳
求解直线和曲线过定点问题的基本解题模板是:把直线或曲线方程中的变量x,y当作常数,把方程一端化为零,既然是过定点,那么这个方程就要对变量的任意一个值都成立,这时变量的系数就要全部等于零,这样就得到一个关于x,y的方程组,这个方程组的解所确定的点就是直线或曲线所过的定点.
跟踪训练1 已知抛物线E:x2=2py(p>0)的焦点为F,A(2,y0)是E上一点,且|AF|=2.
(1)求E的方程;
(2)设点B是E上异于点A的一点,直线AB与直线y=x-3交于点P,过点P作x轴的垂线交E于点M,证明:直线BM过定点.
题型二 定值问题
例2 已知抛物线C:y2=2px经过点P(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(1)求直线l的斜率的取值范围;
(2)设O为原点,=λ=μ,求证:为定值.
方法归纳
解析几何中的定值问题是指某些几何量(线段的长度、图形的面积、角的度数、直线的斜率等)的大小或某些代数表达式的值和题目中的变量无关,始终是一个确定的值,对于定值问题常见的解题模板有两种:
从特殊入手,求出定值,再证明这个值与变量无关;
②可以先研究一下特殊情况,找出定点或定值,再研究一般情况.同时,要掌握巧妙利用特殊值解决相关的定点、定值问题的方法,如将过焦点的弦特殊化,变成垂直于对称轴的弦来研究等.
跟踪训练2 已知O为坐标原点,点F1,F2分别为椭圆M:=1(a>b>0)的左、右焦点,点E(a,b)在抛物线N:x2=y上,直线EF2与椭圆M的一个交点为F,且线段EF的中点恰为F2.
(1)求椭圆M的标准方程;
(2)过抛物线N上一点P且与抛物线N相切的直线l与椭圆M相交于A,B两点,设AB的中点为C,直线OP与直线OC的斜率分别是k1,k2,证明:k1k2为定值.
题型三 最值问题
例3 已知椭圆C:=1(a>b>0)的离心率e=,左顶点为A(-2,0).过点A作直线l交椭圆C于另一点D,交y轴于点E,点O为坐标原点.
(1)求椭圆C的方程;
(2)已知P为AD的中点,是否存在定点Q,对任意的直线l,⊥恒成立?若存在,求出点Q的坐标;若不存在说明理由;
(3)过O点作直线l的平行线与椭圆C相交,M为其中一个交点,求的最大值.
方法归纳
构建关于变量的目标函数,转化为求函数的值域或最值,常利用二次函数的相关知识或基本不等式求解.面积、弦长、含变量的代数式的最值问题,常选用此法,解决问题时要注意自变量的取值范围.
跟踪训练3 顺次连接椭圆C:=1(a>b>0)的四个顶点恰好构成了一个边长为且面积为4的菱形.
(1)求椭圆C的标准方程;
(2)设直线l与椭圆C相切于点A,过点O作OM⊥l,垂足为M,求△AMO面积的最大值.
题型四 范围问题
例4 抛物线C:y=x2,直线l的斜率为2.
(1)若l与C相切,求直线l的方程;
(2)若l与C相交于A,B,线段AB的中垂线交C于P,Q,求的取值范围.
方法归纳
范围问题的解题策略
解决有关范围问题时,先要恰当地引入变量(如点的坐标、角、斜率等),寻找不等关系,其方法有:
1.利用判别式或几何性质来构造不等式,从而确定所求范围;
2.利用已知参数的取值范围,求新参数的范围,解这类问题的核心是在两个参数之间建立相等关系;
3.利用隐含的不等关系建立不等式,从而求出所求范围;
4.利用已知不等关系构造不等式,从而求出所求范围;
5.利用求函数值域的方法将待求量表示为其他变量的函数,求其值域,从而确定所求范围;
6.利用已知,将条件转化为n个不等关系,从而求出参数的范围.
跟踪训练4 已知椭圆C:=1(a>b>0),四点P1(2,0),P2(),P3(1,),P4(-1,)中恰有三点在椭圆上.
(1)求椭圆C的方程;
(2)设不经过左焦点的直线l交椭圆于A,B两点,若直线AF1、l、BF1的斜率依次成等差数列,求直线l的斜率k的取值范围.
章末复习课
考点聚集·分类突破
例1 解析:(1)由题意知解得:
故椭圆C的方程是=1.
(2)由得(4k2+3)x2+8kmx+4m2-12=0.
因为动直线l与椭圆C有且只有一个公共点M(x0,y0),所以m≠0且Δ=0,
即64k2m2-4(4k2+3)(4m2-12)=0,化简得4k2-m2+3=0.①
此时x0=-=-,y0=kx0+m=,所以M(-),由得N(4,4k+m).
假设平面内存在定点P满足条件,由图形对称性知,点P必在x轴上.
设P(x1,0),则·=0对满足①式的m、k恒成立.
因为=(--x1,),=(4-x1,4k+m),由·=0,
得++3=0,
整理得
解得x1=1.
故存在定点P(1,0),使得以MN为直径的圆恒过点P.
跟踪训练1 解析:(1)根据题意知,4=2py0,①
因为|AF|=2,所以y0+=2.②
联立①②解得y0=1,p=2.所以E的方程为x2=4y.
(2)证明:设B(x1,y1),M(x2,y2)
由题意,可设直线BM的方程为y=kx+b,代入x2=4y,得x2-4kx-4b=0.
根与系数的关系.得x1+x2=4k,x1x2=-4b.③
由MP⊥x轴及点P在直线y=x-3上,得P(x2,x2-3),
则由A,P,B三点共线,得=,
整理,得(k-1)x1x2-(2k-4)x1+(b+1)x2-2b-6=0.
将③代入上式并整理,得(2-x1)(2k+b-3)=0.
由点B的任意性,得2k+b-3=0,所以y=kx+3-2k=k(x-2)+3.即直线BM恒过定点(2,3).
例2 解析:(1)因为抛物线y2=2px过点(1,2),所以2p=4,即p=2.
故抛物线C的方程为y2=4x.
由题意知,直线l的斜率存在且不为0.
设直线l的方程为y=kx+1(k≠0).
由得k2x2+(2k-4)x+1=0.
依题意Δ=(2k-4)2-4×k2×1>0,解得k<0或0又PA,PB与y轴相交,故直线l不过点(1,-2).
从而k≠-3.
所以直线l斜率的取值范围是(-∞,-3)
(2)设A(x1,y1),B(x2,y2).
由(1)知x1+x2=-,x1x2=.
直线PA的方程为y-2=(x-1).
令x=0,得点M的纵坐标为yM=+2=+2
同理得点N的纵坐标为yN=+2
由=λ=μ得λ=1-yM,μ=1-yN
所以==
=·=·=2
所以为定值.
跟踪训练2 解析:(1)由题意知F恰为(0,-b)
所以c=,因为a2=b2+c2,所以a2=b2 ①
又点E(a,b)在抛物线N:x2=y上,所以a2=b ②
由①②得a=2,b=,
所以椭圆M的标准方程为=1.
(2)设P(t,),A(x1,y1),B(x2,y2).
因为y=x2,所以y′=x,
则直线AB:y=(x-t)+t2.
将直线AB的方程代入=1得,
12(1+t2)x2-12t3x+3t4-48=0,
所以x1+x2=,y1+y2=(x1+x2)-=.
所以点C(,-),
所以k1=,k2=-,
所以k1k2=-.
例3 解析:(1)∵左顶点为A(-2,0),∴a=2
又∵e=,∴c=,
又∵b2=a2-c2=2,∴椭圆C的标准方程为=1.
(2)由已知,直线l的斜率必存在,直线l的方程为
y=k(x+2),
联立得,(2k2+1)x2+8k2x+8k2-4=0,
设D(x1,y1),A(x2,y2),则x1+x2=,
又P为AD的中点,所以xP=,
又因为点P在直线AD上,则yP=k(xP+2)=,
即点P的坐标为(),
又直线l的方程为y=k(x+2),
令x=0,得点E的坐标为(0,2k),
假设存在定点Q(m,n)使得⊥,则·=0,
①若k=0,=0显然恒成立;
②若k≠0,因为·=0,所以(2m+2)k-n=0
恒成立,
则,即
即定点Q的坐标为(-1,0).
综上,存在定点Q(-1,0)满足题意.
(3)∵OM∥l,∴OM的方程可设为y=kx,
由得M点的横坐标为x=±
由OM∥l,得
=====()≥2=2,当且仅当=即k=±时取等号,
∴当k=±时,的最小值为2.
故的最大值为.
跟踪训练3 解析:(1)由题意可得,解得:
故椭圆C的标准方程为=1;
(2)显然直线l斜率存在且不为0,设直线l:y=kx+t,联立,得(3+4k2)x2+8ktx+4t2-12=0,
且△=64k2t2-4(3+4k2)(4t2-12)=0,得t2=4k2+3,
所以xA==-,
联立,得xM=-,所以|OM|=·=,
则|AM|=·=·=,
所以S△AMO=|AM|·|OM|=··
=·=·,
故△AMO面积最大值为,当且仅当k=±1时成立.
例4 解析:(1)设直线l的方程为y=2x+b.
联立可得x2-2x-b=0,
所以Δ=4+4b=0,所以b=-1,
所以直线l的方程为y=2x-1.
(2)设直线l的方程为y=2x+b,
A(x1,y1),B(x2,y2),P(x3,y3),Q(x4,y4),
联立可得x2-2x-b=0
所以Δ=4+4b>0,b>-1,
x1+x2=2,x1x2=-b,
所以|AB|=|x1-x2|=2,
因为AB的中点为(1,2+b),
所以直线PQ的方程为y=-x++b,
联立可得x2+x--b=0,
所以x3+x4=-,x3x4=--b,
所以|PQ|=|x3-x4|=,
==>,
所以的取值范围为(,+∞).
跟踪训练4 解析:(1)由椭圆的对称性,点P3,P4在椭圆上,代入椭圆,可得=1,
若点P2()在椭圆上,
则有=1,联立无解,
所以点P1(2,0)在椭圆上,代入椭圆,可得a2=4,
代入=1中,解得b2=3,
所以椭圆C的方程为=1.
(2)由(1)可知F1(-1,0),
设直线AB的方程为,
y=kx+m(k≠0),A(x1,y1),B(x2,y2),
联立,
消y,可得(3+4k2)x2+8kmx+4m2-12=0,
则有x1+x2=-,x1x2=,
且Δ=(8km)2-4(3+4k2)(4m2-12)
=48(4k2+3-m2)>0①
由题意可知,
2k===,
化简整理,可得(m-k)(x1+x2+2)=0,
若m-k=0,则直线AB的方程为y=k(x+1),过点F1(-1,0),不满足题意,
所以x1+x2+2=0,即-+2=0,
化简可得,m=k+,
代入①中得,4k2+3>(k+)2,
整理可得16k4+8k2-3>0,
解得k2>,
所以直线l的斜率k的取值范围为k>或k<-.
题型一 定点问题
例1 设椭圆C:=1(a>b>0),F1,F2为左右焦点,B为短轴端点,长轴长为4,焦距为2c,且b>c,△BF1F2的面积为.
(1)求椭圆C的方程;
(2)设动直线l:y=kx+m与椭圆C有且仅有一个公共点M,且与直线x=4相交于点N.试探究:在坐标平面内是否存在定点P,使得以MN为直径的圆恒过点P?若存在求出点P的坐标,若不存在.请说明理由.
方法归纳
求解直线和曲线过定点问题的基本解题模板是:把直线或曲线方程中的变量x,y当作常数,把方程一端化为零,既然是过定点,那么这个方程就要对变量的任意一个值都成立,这时变量的系数就要全部等于零,这样就得到一个关于x,y的方程组,这个方程组的解所确定的点就是直线或曲线所过的定点.
跟踪训练1 已知抛物线E:x2=2py(p>0)的焦点为F,A(2,y0)是E上一点,且|AF|=2.
(1)求E的方程;
(2)设点B是E上异于点A的一点,直线AB与直线y=x-3交于点P,过点P作x轴的垂线交E于点M,证明:直线BM过定点.
题型二 定值问题
例2 已知抛物线C:y2=2px经过点P(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(1)求直线l的斜率的取值范围;
(2)设O为原点,=λ=μ,求证:为定值.
方法归纳
解析几何中的定值问题是指某些几何量(线段的长度、图形的面积、角的度数、直线的斜率等)的大小或某些代数表达式的值和题目中的变量无关,始终是一个确定的值,对于定值问题常见的解题模板有两种:
从特殊入手,求出定值,再证明这个值与变量无关;
②可以先研究一下特殊情况,找出定点或定值,再研究一般情况.同时,要掌握巧妙利用特殊值解决相关的定点、定值问题的方法,如将过焦点的弦特殊化,变成垂直于对称轴的弦来研究等.
跟踪训练2 已知O为坐标原点,点F1,F2分别为椭圆M:=1(a>b>0)的左、右焦点,点E(a,b)在抛物线N:x2=y上,直线EF2与椭圆M的一个交点为F,且线段EF的中点恰为F2.
(1)求椭圆M的标准方程;
(2)过抛物线N上一点P且与抛物线N相切的直线l与椭圆M相交于A,B两点,设AB的中点为C,直线OP与直线OC的斜率分别是k1,k2,证明:k1k2为定值.
题型三 最值问题
例3 已知椭圆C:=1(a>b>0)的离心率e=,左顶点为A(-2,0).过点A作直线l交椭圆C于另一点D,交y轴于点E,点O为坐标原点.
(1)求椭圆C的方程;
(2)已知P为AD的中点,是否存在定点Q,对任意的直线l,⊥恒成立?若存在,求出点Q的坐标;若不存在说明理由;
(3)过O点作直线l的平行线与椭圆C相交,M为其中一个交点,求的最大值.
方法归纳
构建关于变量的目标函数,转化为求函数的值域或最值,常利用二次函数的相关知识或基本不等式求解.面积、弦长、含变量的代数式的最值问题,常选用此法,解决问题时要注意自变量的取值范围.
跟踪训练3 顺次连接椭圆C:=1(a>b>0)的四个顶点恰好构成了一个边长为且面积为4的菱形.
(1)求椭圆C的标准方程;
(2)设直线l与椭圆C相切于点A,过点O作OM⊥l,垂足为M,求△AMO面积的最大值.
题型四 范围问题
例4 抛物线C:y=x2,直线l的斜率为2.
(1)若l与C相切,求直线l的方程;
(2)若l与C相交于A,B,线段AB的中垂线交C于P,Q,求的取值范围.
方法归纳
范围问题的解题策略
解决有关范围问题时,先要恰当地引入变量(如点的坐标、角、斜率等),寻找不等关系,其方法有:
1.利用判别式或几何性质来构造不等式,从而确定所求范围;
2.利用已知参数的取值范围,求新参数的范围,解这类问题的核心是在两个参数之间建立相等关系;
3.利用隐含的不等关系建立不等式,从而求出所求范围;
4.利用已知不等关系构造不等式,从而求出所求范围;
5.利用求函数值域的方法将待求量表示为其他变量的函数,求其值域,从而确定所求范围;
6.利用已知,将条件转化为n个不等关系,从而求出参数的范围.
跟踪训练4 已知椭圆C:=1(a>b>0),四点P1(2,0),P2(),P3(1,),P4(-1,)中恰有三点在椭圆上.
(1)求椭圆C的方程;
(2)设不经过左焦点的直线l交椭圆于A,B两点,若直线AF1、l、BF1的斜率依次成等差数列,求直线l的斜率k的取值范围.
章末复习课
考点聚集·分类突破
例1 解析:(1)由题意知解得:
故椭圆C的方程是=1.
(2)由得(4k2+3)x2+8kmx+4m2-12=0.
因为动直线l与椭圆C有且只有一个公共点M(x0,y0),所以m≠0且Δ=0,
即64k2m2-4(4k2+3)(4m2-12)=0,化简得4k2-m2+3=0.①
此时x0=-=-,y0=kx0+m=,所以M(-),由得N(4,4k+m).
假设平面内存在定点P满足条件,由图形对称性知,点P必在x轴上.
设P(x1,0),则·=0对满足①式的m、k恒成立.
因为=(--x1,),=(4-x1,4k+m),由·=0,
得++3=0,
整理得
解得x1=1.
故存在定点P(1,0),使得以MN为直径的圆恒过点P.
跟踪训练1 解析:(1)根据题意知,4=2py0,①
因为|AF|=2,所以y0+=2.②
联立①②解得y0=1,p=2.所以E的方程为x2=4y.
(2)证明:设B(x1,y1),M(x2,y2)
由题意,可设直线BM的方程为y=kx+b,代入x2=4y,得x2-4kx-4b=0.
根与系数的关系.得x1+x2=4k,x1x2=-4b.③
由MP⊥x轴及点P在直线y=x-3上,得P(x2,x2-3),
则由A,P,B三点共线,得=,
整理,得(k-1)x1x2-(2k-4)x1+(b+1)x2-2b-6=0.
将③代入上式并整理,得(2-x1)(2k+b-3)=0.
由点B的任意性,得2k+b-3=0,所以y=kx+3-2k=k(x-2)+3.即直线BM恒过定点(2,3).
例2 解析:(1)因为抛物线y2=2px过点(1,2),所以2p=4,即p=2.
故抛物线C的方程为y2=4x.
由题意知,直线l的斜率存在且不为0.
设直线l的方程为y=kx+1(k≠0).
由得k2x2+(2k-4)x+1=0.
依题意Δ=(2k-4)2-4×k2×1>0,解得k<0或0
从而k≠-3.
所以直线l斜率的取值范围是(-∞,-3)
(2)设A(x1,y1),B(x2,y2).
由(1)知x1+x2=-,x1x2=.
直线PA的方程为y-2=(x-1).
令x=0,得点M的纵坐标为yM=+2=+2
同理得点N的纵坐标为yN=+2
由=λ=μ得λ=1-yM,μ=1-yN
所以==
=·=·=2
所以为定值.
跟踪训练2 解析:(1)由题意知F恰为(0,-b)
所以c=,因为a2=b2+c2,所以a2=b2 ①
又点E(a,b)在抛物线N:x2=y上,所以a2=b ②
由①②得a=2,b=,
所以椭圆M的标准方程为=1.
(2)设P(t,),A(x1,y1),B(x2,y2).
因为y=x2,所以y′=x,
则直线AB:y=(x-t)+t2.
将直线AB的方程代入=1得,
12(1+t2)x2-12t3x+3t4-48=0,
所以x1+x2=,y1+y2=(x1+x2)-=.
所以点C(,-),
所以k1=,k2=-,
所以k1k2=-.
例3 解析:(1)∵左顶点为A(-2,0),∴a=2
又∵e=,∴c=,
又∵b2=a2-c2=2,∴椭圆C的标准方程为=1.
(2)由已知,直线l的斜率必存在,直线l的方程为
y=k(x+2),
联立得,(2k2+1)x2+8k2x+8k2-4=0,
设D(x1,y1),A(x2,y2),则x1+x2=,
又P为AD的中点,所以xP=,
又因为点P在直线AD上,则yP=k(xP+2)=,
即点P的坐标为(),
又直线l的方程为y=k(x+2),
令x=0,得点E的坐标为(0,2k),
假设存在定点Q(m,n)使得⊥,则·=0,
①若k=0,=0显然恒成立;
②若k≠0,因为·=0,所以(2m+2)k-n=0
恒成立,
则,即
即定点Q的坐标为(-1,0).
综上,存在定点Q(-1,0)满足题意.
(3)∵OM∥l,∴OM的方程可设为y=kx,
由得M点的横坐标为x=±
由OM∥l,得
=====()≥2=2,当且仅当=即k=±时取等号,
∴当k=±时,的最小值为2.
故的最大值为.
跟踪训练3 解析:(1)由题意可得,解得:
故椭圆C的标准方程为=1;
(2)显然直线l斜率存在且不为0,设直线l:y=kx+t,联立,得(3+4k2)x2+8ktx+4t2-12=0,
且△=64k2t2-4(3+4k2)(4t2-12)=0,得t2=4k2+3,
所以xA==-,
联立,得xM=-,所以|OM|=·=,
则|AM|=·=·=,
所以S△AMO=|AM|·|OM|=··
=·=·,
故△AMO面积最大值为,当且仅当k=±1时成立.
例4 解析:(1)设直线l的方程为y=2x+b.
联立可得x2-2x-b=0,
所以Δ=4+4b=0,所以b=-1,
所以直线l的方程为y=2x-1.
(2)设直线l的方程为y=2x+b,
A(x1,y1),B(x2,y2),P(x3,y3),Q(x4,y4),
联立可得x2-2x-b=0
所以Δ=4+4b>0,b>-1,
x1+x2=2,x1x2=-b,
所以|AB|=|x1-x2|=2,
因为AB的中点为(1,2+b),
所以直线PQ的方程为y=-x++b,
联立可得x2+x--b=0,
所以x3+x4=-,x3x4=--b,
所以|PQ|=|x3-x4|=,
==>,
所以的取值范围为(,+∞).
跟踪训练4 解析:(1)由椭圆的对称性,点P3,P4在椭圆上,代入椭圆,可得=1,
若点P2()在椭圆上,
则有=1,联立无解,
所以点P1(2,0)在椭圆上,代入椭圆,可得a2=4,
代入=1中,解得b2=3,
所以椭圆C的方程为=1.
(2)由(1)可知F1(-1,0),
设直线AB的方程为,
y=kx+m(k≠0),A(x1,y1),B(x2,y2),
联立,
消y,可得(3+4k2)x2+8kmx+4m2-12=0,
则有x1+x2=-,x1x2=,
且Δ=(8km)2-4(3+4k2)(4m2-12)
=48(4k2+3-m2)>0①
由题意可知,
2k===,
化简整理,可得(m-k)(x1+x2+2)=0,
若m-k=0,则直线AB的方程为y=k(x+1),过点F1(-1,0),不满足题意,
所以x1+x2+2=0,即-+2=0,
化简可得,m=k+,
代入①中得,4k2+3>(k+)2,
整理可得16k4+8k2-3>0,
解得k2>,
所以直线l的斜率k的取值范围为k>或k<-.
同课章节目录
