沪科版数学八年级下册 19.2三角形的中位线-课件(共14张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 19.2三角形的中位线-课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 08:15:52 | ||
图片预览


文档简介
(共15张PPT)
沪科版数学八年级下册19.2平行四边形
三角形的中位线
C
B
A
F
E
D
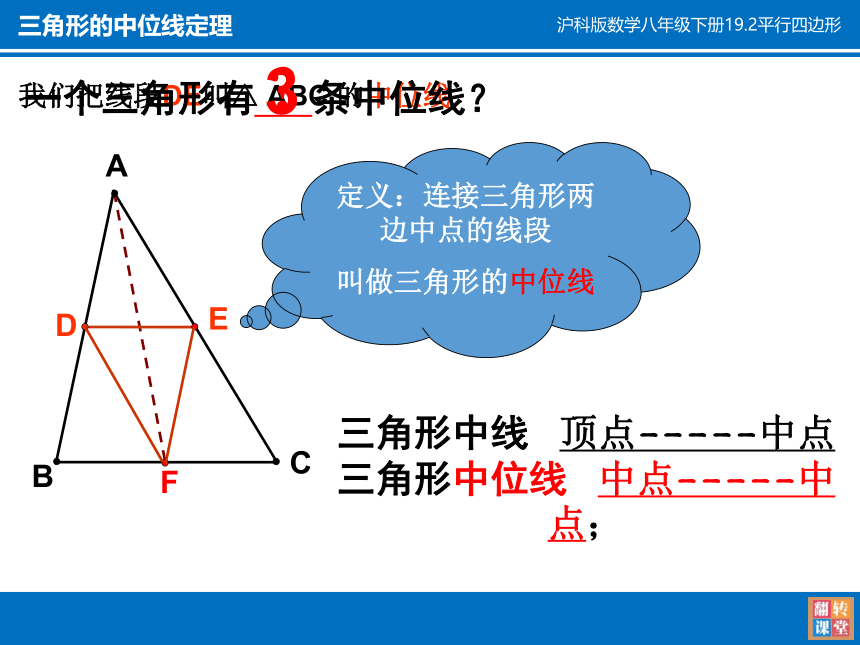
定义:连接三角形两边中点的线段
叫做三角形的中位线
我们把线段DE叫△ ABC 的中位线
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
三角形中线 顶点-----中点
三角形中位线 中点-----中点;
一个三角形有 条中位线?
3
?
A
B
C
D
E
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
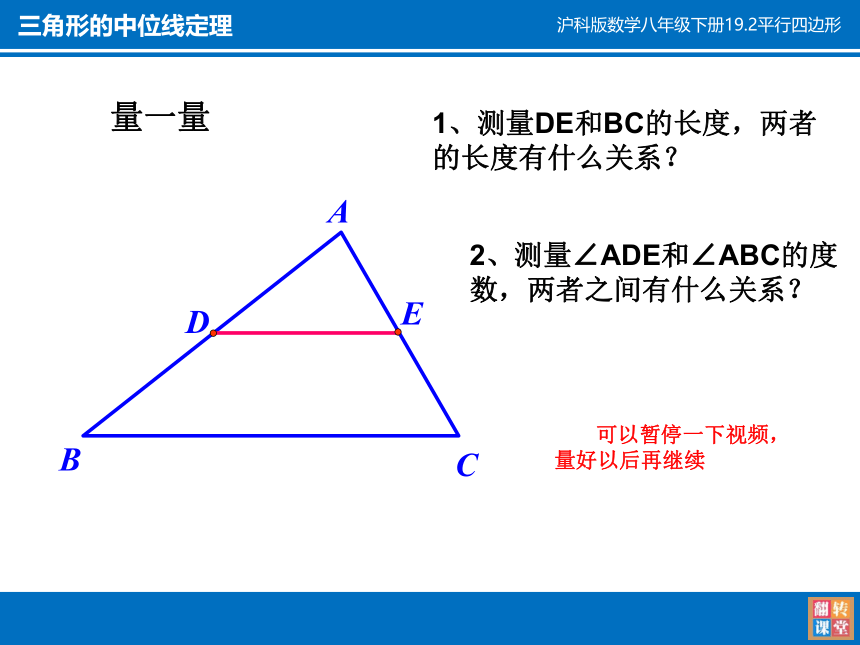
量一量
1、测量DE和BC的长度,两者的长度有什么关系?
2、测量∠ADE和∠ABC的度数,两者之间有什么关系?
可以暂停一下视频,量好以后再继续
A
B
C
D
E
E′
F
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
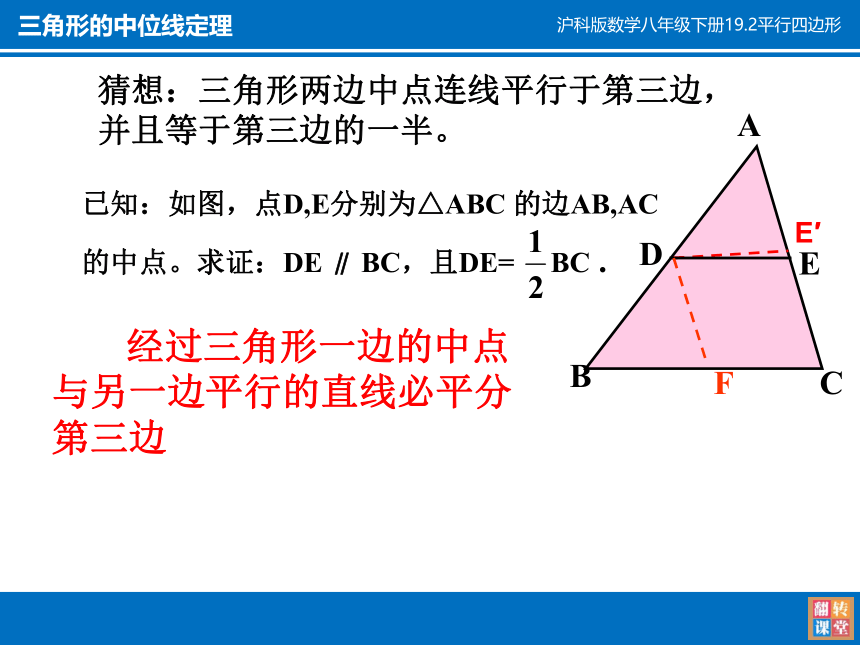
已知:如图,点D,E分别为△ABC 的边AB,AC
的中点。求证:DE ∥ BC,且DE= BC .
经过三角形一边的中点与另一边平行的直线必平分第三边
猜想:三角形两边中点连线平行于第三边,并且等于第三边的一半。
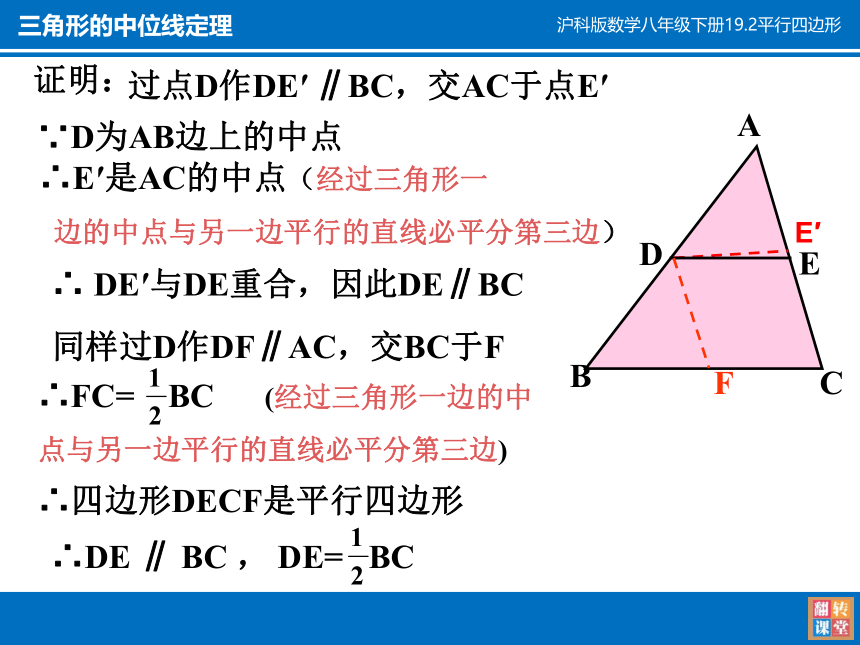
过点D作DE′ ∥BC,交AC于点E′
∵D为AB边上的中点
∴ DE′与DE重合,因此DE∥BC
同样过D作DF∥AC,交BC于F
∴FC= BC (经过三角形一边的中
点与另一边平行的直线必平分第三边)
∴四边形DECF是平行四边形
∴DE ∥ BC , DE= BC
∴E′是AC的中点(经过三角形一
边的中点与另一边平行的直线必平分第三边)
A
B
C
D
E
E′
F
证明:
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
A
B
C
D
E
A
D
E
F
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
探究
请沿着三角形的中位线把三角形裁剪成两部分你能把这两部分拼成一个四边形吗?
四边形BCFD是平行四边形吗?为什么?
A
B
C
D
E
F
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
证明:延 长DE 到 点F,使EF=DE ,
∵DE=EF 、∠AED=∠CEF 、AE=EC
∴△ADE ≌ △CFE
∴AD=CF 、∠A=∠ECF
∴AB∥FC
又AD=DB
∴BD CF
所以 ,四边形BCFD是平行四边形
∴DE ∥ BC 且 DE= BC
已知:如图,点D,E分别为△ABC 的边AB,AC
的中点。求证:DE ∥ BC,且DE= BC .
连结FC.
∵DE是△ABC的中位线
∴⑴ DE∥BC,
① 平行问题
用 途
A
B
C
D
E
三角形中位线定理
三角形两边中点连线平行于第三边,并且等于第三边的一半。
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
位置关系
数量关系
② 一条线段是另一条线段的2倍或
⑵ DE= BC
1.如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么?
2.如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm
图1
图2
60
4
12
A
B
C
D。
。E
B
A
C
D 。
。E
。F
5
4
3
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
应用:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是平行四边形。
A
B
C
D
E
F
G
H
∴ EF//HG,EF=HG
∴四边形EFGH是平行四边形
证明:连接AC,
在△ABC中,
在△ADC中,同理可得
HG//AC,HG= AC
∵E、F分别是AB、BC边的中点,即EF是△ABC的中位线.
∴EF//AC,EF= AC
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
转化思想
三角形的中位线
沪科版数学八年级下册19.2平行四边形
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
试一试
如图,点E,F,G,H分别是CD,BC,AB,DA的中点。 求证:四边形EFGH是平行四边形。
三角形的中位线
沪科版数学八年级下册19.2平行四边形
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
小结
1、三角形的中位线
三角形中位线定理
2、探索——发现——猜想——证明
3、转化、对比、归纳
4、发散思维
三角形的中位线
沪科版数学八年级下册19.2平行四边形
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
作业
1、 (必做题)已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点. 求证:四边形DEFG是平行四边形
2、(选做题)已知平行四边形ABCD中,AC、BD交于点O,E、F、G、H分别是AB、OB、CD、OD的中点。
求证:∠HEF=∠FGH.
再见
沪科版数学八年级下册19.2平行四边形
三角形的中位线
C
B
A
F
E
D
定义:连接三角形两边中点的线段
叫做三角形的中位线
我们把线段DE叫△ ABC 的中位线
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
三角形中线 顶点-----中点
三角形中位线 中点-----中点;
一个三角形有 条中位线?
3
?
A
B
C
D
E
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
量一量
1、测量DE和BC的长度,两者的长度有什么关系?
2、测量∠ADE和∠ABC的度数,两者之间有什么关系?
可以暂停一下视频,量好以后再继续
A
B
C
D
E
E′
F
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
已知:如图,点D,E分别为△ABC 的边AB,AC
的中点。求证:DE ∥ BC,且DE= BC .
经过三角形一边的中点与另一边平行的直线必平分第三边
猜想:三角形两边中点连线平行于第三边,并且等于第三边的一半。
过点D作DE′ ∥BC,交AC于点E′
∵D为AB边上的中点
∴ DE′与DE重合,因此DE∥BC
同样过D作DF∥AC,交BC于F
∴FC= BC (经过三角形一边的中
点与另一边平行的直线必平分第三边)
∴四边形DECF是平行四边形
∴DE ∥ BC , DE= BC
∴E′是AC的中点(经过三角形一
边的中点与另一边平行的直线必平分第三边)
A
B
C
D
E
E′
F
证明:
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
A
B
C
D
E
A
D
E
F
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
探究
请沿着三角形的中位线把三角形裁剪成两部分你能把这两部分拼成一个四边形吗?
四边形BCFD是平行四边形吗?为什么?
A
B
C
D
E
F
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
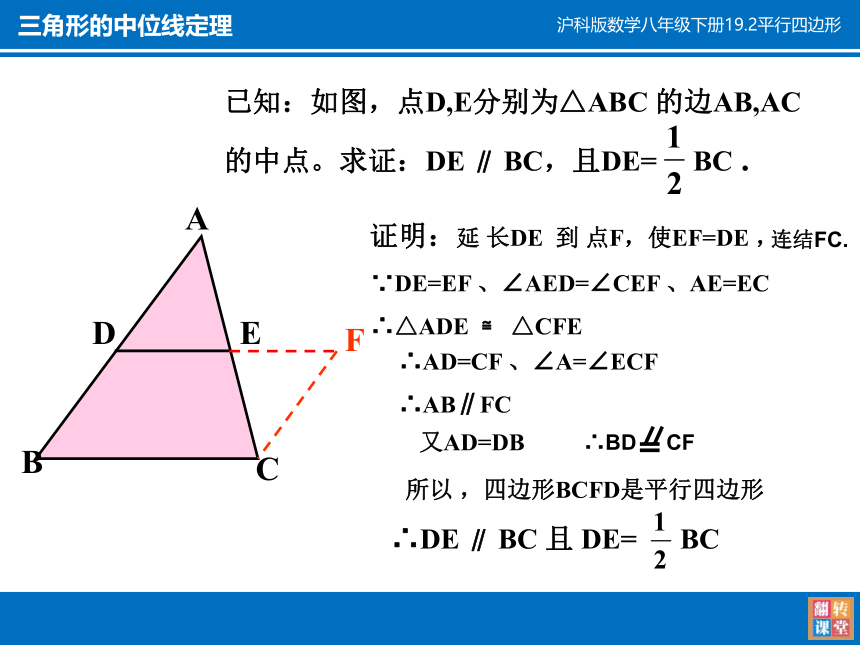
证明:延 长DE 到 点F,使EF=DE ,
∵DE=EF 、∠AED=∠CEF 、AE=EC
∴△ADE ≌ △CFE
∴AD=CF 、∠A=∠ECF
∴AB∥FC
又AD=DB
∴BD CF
所以 ,四边形BCFD是平行四边形
∴DE ∥ BC 且 DE= BC
已知:如图,点D,E分别为△ABC 的边AB,AC
的中点。求证:DE ∥ BC,且DE= BC .
连结FC.
∵DE是△ABC的中位线
∴⑴ DE∥BC,
① 平行问题
用 途
A
B
C
D
E
三角形中位线定理
三角形两边中点连线平行于第三边,并且等于第三边的一半。
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
位置关系
数量关系
② 一条线段是另一条线段的2倍或
⑵ DE= BC
1.如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么?
2.如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm
图1
图2
60
4
12
A
B
C
D。
。E
B
A
C
D 。
。E
。F
5
4
3
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
应用:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是平行四边形。
A
B
C
D
E
F
G
H
∴ EF//HG,EF=HG
∴四边形EFGH是平行四边形
证明:连接AC,
在△ABC中,
在△ADC中,同理可得
HG//AC,HG= AC
∵E、F分别是AB、BC边的中点,即EF是△ABC的中位线.
∴EF//AC,EF= AC
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
转化思想
三角形的中位线
沪科版数学八年级下册19.2平行四边形
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
试一试
如图,点E,F,G,H分别是CD,BC,AB,DA的中点。 求证:四边形EFGH是平行四边形。
三角形的中位线
沪科版数学八年级下册19.2平行四边形
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
小结
1、三角形的中位线
三角形中位线定理
2、探索——发现——猜想——证明
3、转化、对比、归纳
4、发散思维
三角形的中位线
沪科版数学八年级下册19.2平行四边形
三角形的中位线定理
沪科版数学八年级下册19.2平行四边形
作业
1、 (必做题)已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点. 求证:四边形DEFG是平行四边形
2、(选做题)已知平行四边形ABCD中,AC、BD交于点O,E、F、G、H分别是AB、OB、CD、OD的中点。
求证:∠HEF=∠FGH.
再见
