四年级上册数学西师大版2.2加法运算律课件(共19张PPT)
文档属性
| 名称 | 四年级上册数学西师大版2.2加法运算律课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 00:00:00 | ||
图片预览




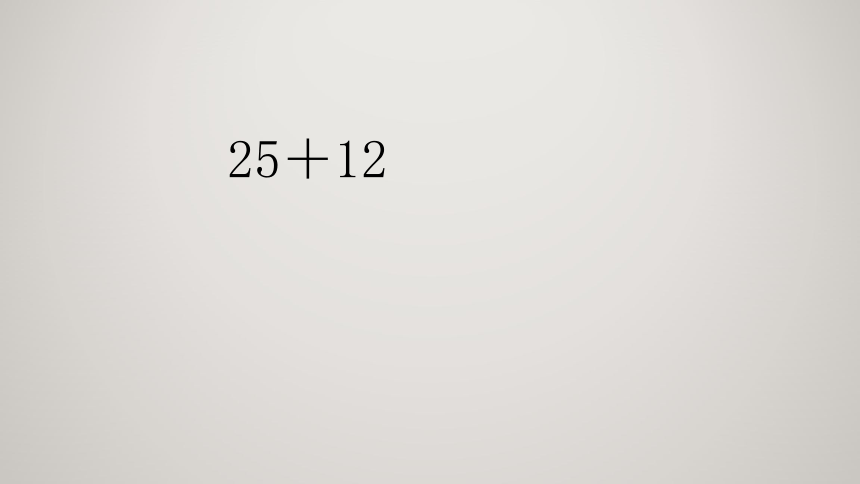


文档简介
(共19张PPT)
加法运算律
教学目标教学目标
本节课我们主要来学习加法的运算定律,同学们要掌握加法交换律、加法结合律的内容,能够熟练的应用加法的交换律和结合律解决实际的问题。
1200+650
12+25
25+12
500+300
300+500
30+20
20+30
650+1200
=37
=50
=800
=1850
=37
=800
=50
=1850
温馨提示:
1、先自己算一算
2、小组讨论交流:小松鼠为什么算的这样快?它究竟用了什么办法很快就算出来了?小松鼠的计算方法和你的计算方法一样吗?
作为老师,是否认识到这种举例说明或逐一验证无法说明运算律普遍成立?
有哪些更充足的理由?这些理由对“意义理解”有什么帮助?
将规律性知识的教学统一归结到——“规律的发现与检验”,是否要考虑不同的内容应有不同的教学重点?
规律性知识的教学
有了猜想,还需要验证,这样得出的结论才准确。举的例子要尽可能的多,还要尽可能包含一些特殊的例子。
发现(猜想)→举例验证→应用
普遍存在的一种模式:
25+12
像这样的式子多吗?能写完吗?可是如果想写完怎么办?
1200+650
12+25
25+12
500+300
300+500
30+20
20+30
650+1200
=
=
=
=
a+b
b+a
=
定义1 (序数理论):如果数a与数b都是自然数,在自然数列中的数a之后再数出b个数来,恰好对应于自然数列中的数c,那么,数c叫做a与b的和,求两个数的和的运算叫做加法。记作:a+b=c 读作“a加b等于c”。
a与b都叫做加数,符号“+”叫做加号。
定义2(基数理论):设A、B是两个不相交的有限集合,它们的基数分别是a和b,如果集合A与B合并所得的并集是C,那么并集C的基数c就叫做a与b的和,求两个数的和的运算叫做加法。记作:a+b=c 读作“a加b等于c”。
a与b都叫做加数,符号“+”叫做加号。
把两个数合并成一个数的运算,叫做加法。
30+20
89 + 96 + 104
89 + 96 + 104
=185 +104
=289
=89 +200
=289
( )
289
加法交换律
● ● ● ● ● ● ● ● + ● ● ● ● ●
“+”号的左右两边分别排列着一些点,用数数的方法我们可以得到它的总数。
从左至右数它们→8 + 5 ( )
从右到左数它们→5 + 8 ( )
只要每个点都数到,而且每个点只数一次,那么两次数的结果,就不会因为数数时的顺序不同而改变。
650+1200
运算律 字母表示式 变 没变
加法交换律
加法结合律
教算术也教代数
著名数学家、数学教育家项武义:
运算律是代数学的基础
“=”意义的扩展;
字母表示变化的数量;
由算术的程序思维”到“代数的关系思维”。
加法验算
357+218=575
357
+218
575
218
+357
575
验算:
4 + 3 = 7
3 + 4 = 7
4 + 3 = 3 + 4
等号表示结果
等号表示“4+3”和“3+4”是等价的(和不变)
2÷4
4÷2
≠
运算律 字母表示式 变 没变
加法交换律 a+b=b+a 位置 数据、运算符号、结果
加法结合律 (a+b)+c =a+(b+c) 计算顺序 数据、运算符号、 结果、位置
讨论:
89+96+104
89+(96+104)
=
153+315+85
153+(315+85)
=
1.说一说,你们能发现什么规律?
2.写一写,再写出两个这样的式子,
验证你们所发现的规律。
1、这节课我们学到哪些知识?
2、这些知识给我们带来了什么好处?
3、你还有哪些疑问?
谢谢
加法运算律
教学目标教学目标
本节课我们主要来学习加法的运算定律,同学们要掌握加法交换律、加法结合律的内容,能够熟练的应用加法的交换律和结合律解决实际的问题。
1200+650
12+25
25+12
500+300
300+500
30+20
20+30
650+1200
=37
=50
=800
=1850
=37
=800
=50
=1850
温馨提示:
1、先自己算一算
2、小组讨论交流:小松鼠为什么算的这样快?它究竟用了什么办法很快就算出来了?小松鼠的计算方法和你的计算方法一样吗?
作为老师,是否认识到这种举例说明或逐一验证无法说明运算律普遍成立?
有哪些更充足的理由?这些理由对“意义理解”有什么帮助?
将规律性知识的教学统一归结到——“规律的发现与检验”,是否要考虑不同的内容应有不同的教学重点?
规律性知识的教学
有了猜想,还需要验证,这样得出的结论才准确。举的例子要尽可能的多,还要尽可能包含一些特殊的例子。
发现(猜想)→举例验证→应用
普遍存在的一种模式:
25+12
像这样的式子多吗?能写完吗?可是如果想写完怎么办?
1200+650
12+25
25+12
500+300
300+500
30+20
20+30
650+1200
=
=
=
=
a+b
b+a
=
定义1 (序数理论):如果数a与数b都是自然数,在自然数列中的数a之后再数出b个数来,恰好对应于自然数列中的数c,那么,数c叫做a与b的和,求两个数的和的运算叫做加法。记作:a+b=c 读作“a加b等于c”。
a与b都叫做加数,符号“+”叫做加号。
定义2(基数理论):设A、B是两个不相交的有限集合,它们的基数分别是a和b,如果集合A与B合并所得的并集是C,那么并集C的基数c就叫做a与b的和,求两个数的和的运算叫做加法。记作:a+b=c 读作“a加b等于c”。
a与b都叫做加数,符号“+”叫做加号。
把两个数合并成一个数的运算,叫做加法。
30+20
89 + 96 + 104
89 + 96 + 104
=185 +104
=289
=89 +200
=289
( )
289
加法交换律
● ● ● ● ● ● ● ● + ● ● ● ● ●
“+”号的左右两边分别排列着一些点,用数数的方法我们可以得到它的总数。
从左至右数它们→8 + 5 ( )
从右到左数它们→5 + 8 ( )
只要每个点都数到,而且每个点只数一次,那么两次数的结果,就不会因为数数时的顺序不同而改变。
650+1200
运算律 字母表示式 变 没变
加法交换律
加法结合律
教算术也教代数
著名数学家、数学教育家项武义:
运算律是代数学的基础
“=”意义的扩展;
字母表示变化的数量;
由算术的程序思维”到“代数的关系思维”。
加法验算
357+218=575
357
+218
575
218
+357
575
验算:
4 + 3 = 7
3 + 4 = 7
4 + 3 = 3 + 4
等号表示结果
等号表示“4+3”和“3+4”是等价的(和不变)
2÷4
4÷2
≠
运算律 字母表示式 变 没变
加法交换律 a+b=b+a 位置 数据、运算符号、结果
加法结合律 (a+b)+c =a+(b+c) 计算顺序 数据、运算符号、 结果、位置
讨论:
89+96+104
89+(96+104)
=
153+315+85
153+(315+85)
=
1.说一说,你们能发现什么规律?
2.写一写,再写出两个这样的式子,
验证你们所发现的规律。
1、这节课我们学到哪些知识?
2、这些知识给我们带来了什么好处?
3、你还有哪些疑问?
谢谢
