沪科版数学八年级下册 第19章 四边形复习 课件(共13张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 第19章 四边形复习 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 13:49:48 | ||
图片预览



文档简介
(共13张PPT)
知识回顾练习:
1.已知□ABCD中,∠B=70°,则∠A=__,∠C=___,∠D=____.
2.在□ABCD中,AB=3,BC=4,则□ABCD的周长等于_______.
3.不能判定四边形ABCD为平行四边形的题设是( )
A.AB=CD,AD=BC B.AB=CD AB∥CD
C.AB=CD,AD∥BC D.AB∥CD,AD∥BC
4.菱形的周长为100 cm,一条对角线长为14 cm,它的面积是_______.
5.下列条件中,能判定四边形是菱形的是( ).
A.两组对边分别相等 B.两条对角线互相平分且相等
C.两条对角线相等且互相垂直 D.两条对角线互相垂直平分
6.如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=2,则AC的长为______.矩形ABCD的面积是_______.
7.四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( ).
A.AB=CD B.AD=BC C.AB=BC D.AC=BD
8.四边形ABCD的对角线AC、BD交于点O,能判定它是正方形的是( ).
A.AO=OC,OB=OD B.AO=BO=CO=DO,AC⊥BD
C.AO=OC,OB=OD,AC⊥BD D.AO=OC=OB=OD
6题图
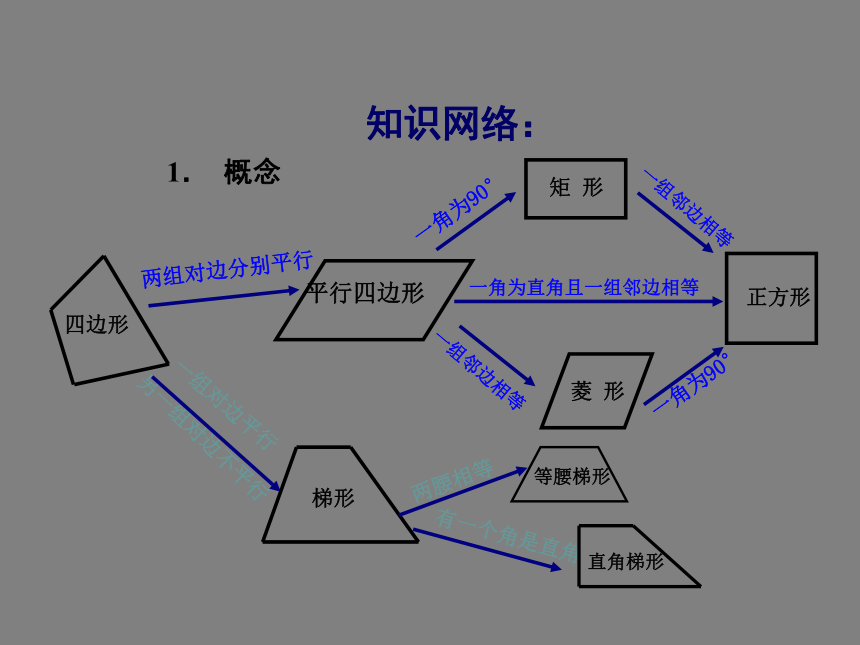
四边形
平行四边形
矩 形
菱 形
一角为90°
正方形
两组对边分别平行
一角为直角且一组邻边相等
一组邻边相等
一组邻边相等
一角为90°
知识网络:
1. 概念
一组对边平行
另一组对边不平行
梯形
两腰相等
有一个角是直角
等腰梯形
直角梯形
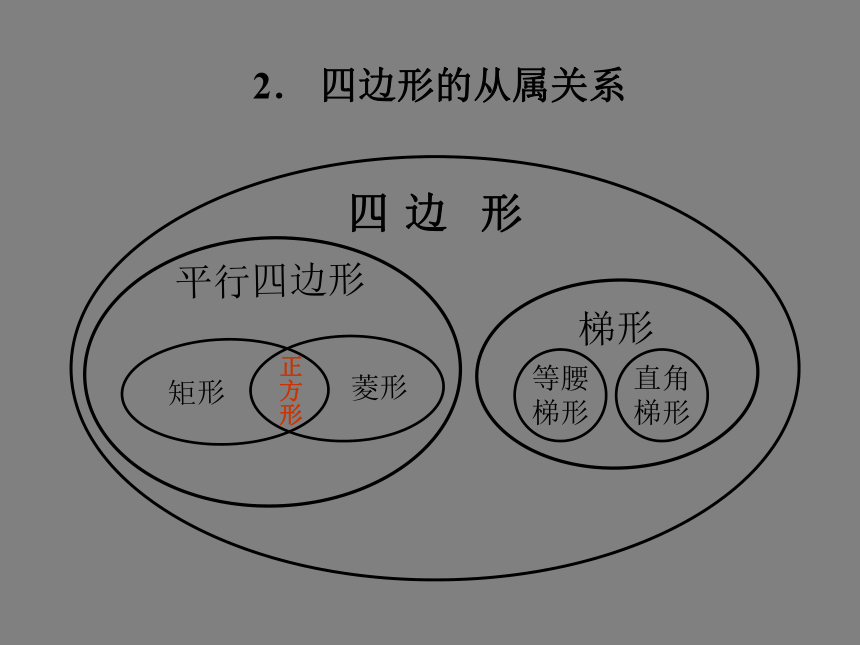
边 形
平行四边形
矩形
菱形
2. 四边形的从属关系
梯形
等腰
梯形
直角
梯形
正方形
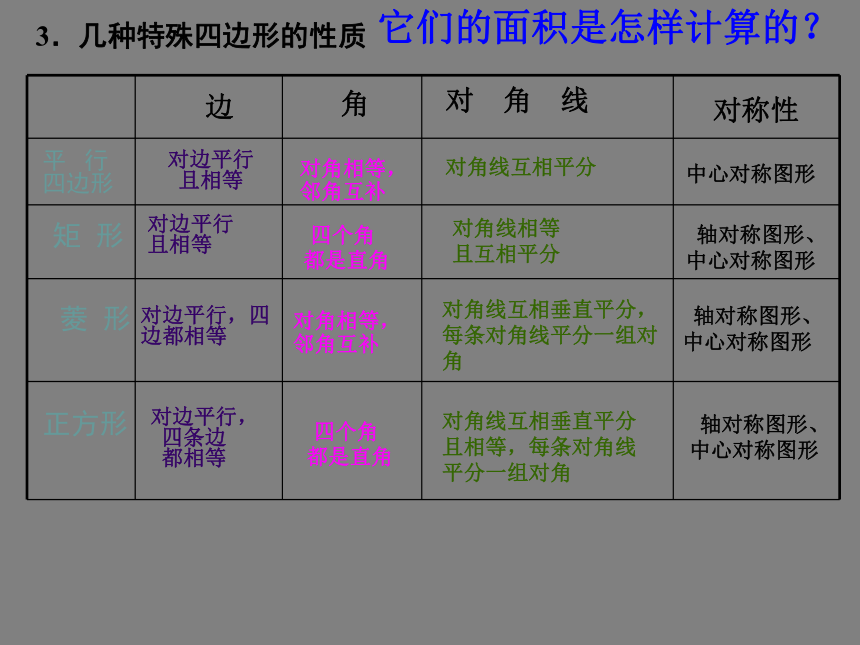
3.几种特殊四边形的性质
平 行
四边形
矩 形
菱 形
正方形
边
对边平行
且相等
对边平行
且相等
对边平行,四边都相等
对边平行,
四条边
都相等
角
对角相等,
邻角互补
四个角
都是直角
对角相等,
邻角互补
四个角
都是直角
对 角 线
对角线互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
对角线互相垂直平分且相等,每条对角线平分一组对角
对称性
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
它们的面积是怎样计算的?
4.特殊四边形的常用判定方法
平 行
四边形
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(4)两组对角分别相等的四边形是平行四边形;
(5)对角线互相平分的四边形是平行四边形;
(3)一组对边平行且相等的四边形是平行四边形.
矩 形
(1)有一个角是直角的平行四边形是矩形;
(3)有三个角是直角的四边形是矩形;
(2)对角线相等的平行四边形是矩形.
菱 形
(1)有一组邻边相等的平行四边形是菱形;
(3)四条边都相等的四边形是菱形;
(2)对角线互相垂直的平行四边形是菱形.
正方形
(2)有一组邻边相等的矩形是正方形;
(3)有一个角是直角的菱形是正方形.
(1)一个角是直角且一组邻边相等的平行四边形是正方形;
关于中点四边形
一个四边形四边中点所连得到的四边形叫做中点四边形,它的形状仅仅与原来四边形的 有关。
1、连接任意一个四边形四边中点所得到的四边形一定是 。
4、连接任意一个矩形四边中点所得到的四边形是 。
3、连接任意一个菱形四边中点所得到的四边形是 。
2、连接任意一个平行四边形四边中点所得到的四边形是 。
5、连接任意一个正方形四边中点所得到的四边形是 。
平行四边形
平行四边形
矩形
菱形
正方形
6、连接任意一个等腰梯形四边中点所得到的四边形是 。
菱形
对角线
例1、如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合)且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是 .
2.5
我想到:
2、平行四边形被对角线分成的四个三角形面积相等.
例题精选:
1、菱形面积等于对角线乘积的一半
例2、如图,矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且 DP=OC,连结CP,试判断四边形CODP的形状.
A
B
D
C
O
P
解:四边形CODP是菱形
∵ DP∥OC, DP=OC,
∴ 四边形CODP是平行四边形.
∵四边形ABCD是矩形 ,
∴CO=DO.
∴四边形CODP是菱形 .
如果题目中的矩形变为正方形(图二),结论又应变为什么?
如果题目中的矩形变为菱形(图一),结论应变为什么?
图一
A
O
D
P
B
C
P
C
D
O
B
A
图二
A
B
D
C
O
P
例3、 如图,矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且 DP=OC,连结CP,试判断四边形CODP的形状.
当∠BAC等于 时,四边形ADFE是矩形;
当∠BAC等于 时,平行四边形ADFE不存在;
当△ABC分别满足什么条件时,平行四边形是菱形、正方形.
小试牛刀:
1、以△ABC的边AB、AC为边作等边△ABD和等边△ ACE,四边形ADFE是平行四边形.
解: ③ AB=AC时,平行四边形ADFE时菱形.
AB=AC且∠BAC=150°时,平行四边形ADFE是正方形.
150°
60°
B
C
A
E
F
D
60°
60°
2、已知△ABC中,D是AB的中点,E是AC上的点,且∠ABE=∠BAC,EF∥AB,DF∥BE,请猜想DF与AE有怎样的特殊关系,并说明理由.
A
E
D
F
C
B
知识回顾练习:
1.已知□ABCD中,∠B=70°,则∠A=__,∠C=___,∠D=____.
2.在□ABCD中,AB=3,BC=4,则□ABCD的周长等于_______.
3.不能判定四边形ABCD为平行四边形的题设是( )
A.AB=CD,AD=BC B.AB=CD AB∥CD
C.AB=CD,AD∥BC D.AB∥CD,AD∥BC
4.菱形的周长为100 cm,一条对角线长为14 cm,它的面积是_______.
5.下列条件中,能判定四边形是菱形的是( ).
A.两组对边分别相等 B.两条对角线互相平分且相等
C.两条对角线相等且互相垂直 D.两条对角线互相垂直平分
6.如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=2,则AC的长为______.矩形ABCD的面积是_______.
7.四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( ).
A.AB=CD B.AD=BC C.AB=BC D.AC=BD
8.四边形ABCD的对角线AC、BD交于点O,能判定它是正方形的是( ).
A.AO=OC,OB=OD B.AO=BO=CO=DO,AC⊥BD
C.AO=OC,OB=OD,AC⊥BD D.AO=OC=OB=OD
6题图
四边形
平行四边形
矩 形
菱 形
一角为90°
正方形
两组对边分别平行
一角为直角且一组邻边相等
一组邻边相等
一组邻边相等
一角为90°
知识网络:
1. 概念
一组对边平行
另一组对边不平行
梯形
两腰相等
有一个角是直角
等腰梯形
直角梯形
边 形
平行四边形
矩形
菱形
2. 四边形的从属关系
梯形
等腰
梯形
直角
梯形
正方形
3.几种特殊四边形的性质
平 行
四边形
矩 形
菱 形
正方形
边
对边平行
且相等
对边平行
且相等
对边平行,四边都相等
对边平行,
四条边
都相等
角
对角相等,
邻角互补
四个角
都是直角
对角相等,
邻角互补
四个角
都是直角
对 角 线
对角线互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
对角线互相垂直平分且相等,每条对角线平分一组对角
对称性
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
它们的面积是怎样计算的?
4.特殊四边形的常用判定方法
平 行
四边形
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(4)两组对角分别相等的四边形是平行四边形;
(5)对角线互相平分的四边形是平行四边形;
(3)一组对边平行且相等的四边形是平行四边形.
矩 形
(1)有一个角是直角的平行四边形是矩形;
(3)有三个角是直角的四边形是矩形;
(2)对角线相等的平行四边形是矩形.
菱 形
(1)有一组邻边相等的平行四边形是菱形;
(3)四条边都相等的四边形是菱形;
(2)对角线互相垂直的平行四边形是菱形.
正方形
(2)有一组邻边相等的矩形是正方形;
(3)有一个角是直角的菱形是正方形.
(1)一个角是直角且一组邻边相等的平行四边形是正方形;
关于中点四边形
一个四边形四边中点所连得到的四边形叫做中点四边形,它的形状仅仅与原来四边形的 有关。
1、连接任意一个四边形四边中点所得到的四边形一定是 。
4、连接任意一个矩形四边中点所得到的四边形是 。
3、连接任意一个菱形四边中点所得到的四边形是 。
2、连接任意一个平行四边形四边中点所得到的四边形是 。
5、连接任意一个正方形四边中点所得到的四边形是 。
平行四边形
平行四边形
矩形
菱形
正方形
6、连接任意一个等腰梯形四边中点所得到的四边形是 。
菱形
对角线
例1、如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合)且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是 .
2.5
我想到:
2、平行四边形被对角线分成的四个三角形面积相等.
例题精选:
1、菱形面积等于对角线乘积的一半
例2、如图,矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且 DP=OC,连结CP,试判断四边形CODP的形状.
A
B
D
C
O
P
解:四边形CODP是菱形
∵ DP∥OC, DP=OC,
∴ 四边形CODP是平行四边形.
∵四边形ABCD是矩形 ,
∴CO=DO.
∴四边形CODP是菱形 .
如果题目中的矩形变为正方形(图二),结论又应变为什么?
如果题目中的矩形变为菱形(图一),结论应变为什么?
图一
A
O
D
P
B
C
P
C
D
O
B
A
图二
A
B
D
C
O
P
例3、 如图,矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且 DP=OC,连结CP,试判断四边形CODP的形状.
当∠BAC等于 时,四边形ADFE是矩形;
当∠BAC等于 时,平行四边形ADFE不存在;
当△ABC分别满足什么条件时,平行四边形是菱形、正方形.
小试牛刀:
1、以△ABC的边AB、AC为边作等边△ABD和等边△ ACE,四边形ADFE是平行四边形.
解: ③ AB=AC时,平行四边形ADFE时菱形.
AB=AC且∠BAC=150°时,平行四边形ADFE是正方形.
150°
60°
B
C
A
E
F
D
60°
60°
2、已知△ABC中,D是AB的中点,E是AC上的点,且∠ABE=∠BAC,EF∥AB,DF∥BE,请猜想DF与AE有怎样的特殊关系,并说明理由.
A
E
D
F
C
B
