综合与实践:多边形内角和(课件)四年级下册数学苏教版(共16张PPT)
文档属性
| 名称 | 综合与实践:多边形内角和(课件)四年级下册数学苏教版(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 10:00:30 | ||
图片预览



文档简介
(共16张PPT)
义务教育教科书苏教版数学四年级下册
综合与实践
多边形的内角和
情境导入
你知道三角形的内角和是多少吗?你是怎么求的?
三角形3个内角的和是180°,四边形、五边形、六边形等多边形的内角和呢?
情境导入
你能想办法求出下面四边形4个内角的和吗?
要求多边形的内角和,就是求每一个内角度数的总和。
活动探究
活动探究
140°
40°
先量出每个角的度数,再求和。
90°+ 90°+140°+ 40°=360°
你能用不同的方法求内角和吗?
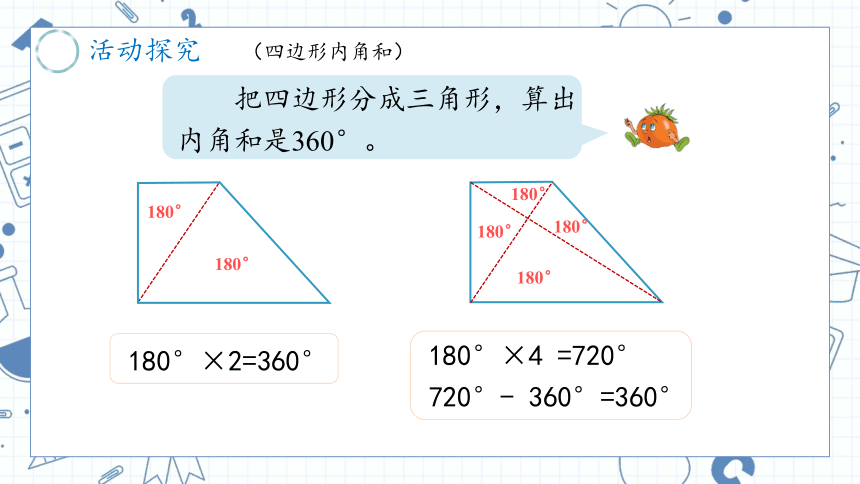
把四边形分成三角形,算出内角和是360°。
180°×2=360°
活动探究
180°
180°
180°
180°
180°
180°
180°×4 =720°
720°- 360°=360°
(四边形内角和)
活动探究
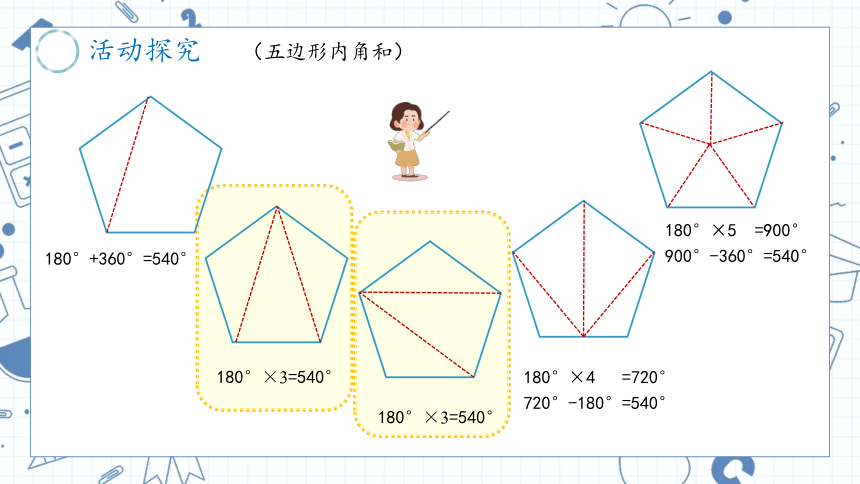
(五边形内角和)
180°+360°=540°
180°×3=540°
180°×3=540°
180°×4 =720°
720°-180°=540°
180°×5 =900°
900°-360°=540°
五边形最少可以分成3个三角形。
活动探究
180°×3=540°
六边形最少可以分成4个三角形。
180°×4=720°
活动探究
其他多边形也可以像这样分成几个三角形来计算内角和吗?
小组合作,任意画一些多边形,试一试。
最少5个三角形
180°×5=900°
最少6个三角形
七边形
八边形
180°×6=1080°
规律探究
图形名称 边数 分成的三角形个数 内角和
三角形 3 1 180°
四边形 4 2 180°×2
五边形
六边形
七边形
八边形
…… …… …… ……
5
3
180°×3
6
4
180°×4
7
5
180°×5
8
6
180°×6
仔细观察表中数据,看看能发现什么规律!
规律探究
可以把多边形分成若干个三角形,计算它的内角和;
分成的三角形个数都比多边形的边数少2;
分成了几个三角形,多边形的内角和就有几个180°。
你会用算式把发现的规律表现出来吗?
规律探究
用一个式子表示多边形内角和的计算方法:
多边形内角和=(多边形的边数 2)×180°
n边形内角和=(n 2)×180°
课堂练习
1、求十边形的内角和的度数?那十二边形的度数又是多少呢?
[提示: n边形的内角和= (n-2)×180°]
解:(10-2)×180°=1440°
(12-2)×180°=1800°
答:十边形的内角和是1440°,十二边形的内角和是1800°
课堂练习
2、已知一个多边形的内角和等于1620°,求它是几边形?
[提示: n边形的内角和= (n-2)×180°]
(n-2)×180°=1620°
1620°÷180 = 9
9+2=11
解得 n=11
答:这个多边形是十一边形°
课堂小结
(1)多边形的内角和可以根据三角形的内角
和推算出来。
(2)从简单的问题想起、有序思考,是探索
规律的有效方法。
(3)可以把新的问题转化为能够解决的问题。
下课啦!
义务教育教科书苏教版数学四年级下册
综合与实践
多边形的内角和
情境导入
你知道三角形的内角和是多少吗?你是怎么求的?
三角形3个内角的和是180°,四边形、五边形、六边形等多边形的内角和呢?
情境导入
你能想办法求出下面四边形4个内角的和吗?
要求多边形的内角和,就是求每一个内角度数的总和。
活动探究
活动探究
140°
40°
先量出每个角的度数,再求和。
90°+ 90°+140°+ 40°=360°
你能用不同的方法求内角和吗?
把四边形分成三角形,算出内角和是360°。
180°×2=360°
活动探究
180°
180°
180°
180°
180°
180°
180°×4 =720°
720°- 360°=360°
(四边形内角和)
活动探究
(五边形内角和)
180°+360°=540°
180°×3=540°
180°×3=540°
180°×4 =720°
720°-180°=540°
180°×5 =900°
900°-360°=540°
五边形最少可以分成3个三角形。
活动探究
180°×3=540°
六边形最少可以分成4个三角形。
180°×4=720°
活动探究
其他多边形也可以像这样分成几个三角形来计算内角和吗?
小组合作,任意画一些多边形,试一试。
最少5个三角形
180°×5=900°
最少6个三角形
七边形
八边形
180°×6=1080°
规律探究
图形名称 边数 分成的三角形个数 内角和
三角形 3 1 180°
四边形 4 2 180°×2
五边形
六边形
七边形
八边形
…… …… …… ……
5
3
180°×3
6
4
180°×4
7
5
180°×5
8
6
180°×6
仔细观察表中数据,看看能发现什么规律!
规律探究
可以把多边形分成若干个三角形,计算它的内角和;
分成的三角形个数都比多边形的边数少2;
分成了几个三角形,多边形的内角和就有几个180°。
你会用算式把发现的规律表现出来吗?
规律探究
用一个式子表示多边形内角和的计算方法:
多边形内角和=(多边形的边数 2)×180°
n边形内角和=(n 2)×180°
课堂练习
1、求十边形的内角和的度数?那十二边形的度数又是多少呢?
[提示: n边形的内角和= (n-2)×180°]
解:(10-2)×180°=1440°
(12-2)×180°=1800°
答:十边形的内角和是1440°,十二边形的内角和是1800°
课堂练习
2、已知一个多边形的内角和等于1620°,求它是几边形?
[提示: n边形的内角和= (n-2)×180°]
(n-2)×180°=1620°
1620°÷180 = 9
9+2=11
解得 n=11
答:这个多边形是十一边形°
课堂小结
(1)多边形的内角和可以根据三角形的内角
和推算出来。
(2)从简单的问题想起、有序思考,是探索
规律的有效方法。
(3)可以把新的问题转化为能够解决的问题。
下课啦!
