沪科版数学八年级下册 19.1 多边形内角和-教案
文档属性
| 名称 | 沪科版数学八年级下册 19.1 多边形内角和-教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 33.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 00:00:00 | ||
图片预览

文档简介
19.1多边形内角和
学习目标:
1、了解多边形及相关概念。
2、掌握多边形的内角和公式,并会运用它进行有关计算。
学习重点:多边形的内角和公式。
学习难点:多边形的内角和公式的推理方法。
一、独学:阅读课本70、71页,完成下列填空。
1、在平面内,由若干条不在( )的线段( )所组成的封闭图形,叫做多边形。
2、组成多边形的( )叫做多边形的边。
3、相邻两边的( )叫做多边形的顶点。
4、多边形中( )组成的角叫做多边形的内角,简称多边形的角。
5、在顶点处一边与另一边的延长线所组成的角叫做多边形的( ).
6、多边形中连接不相邻两个顶点的线段叫做多边形的( )。
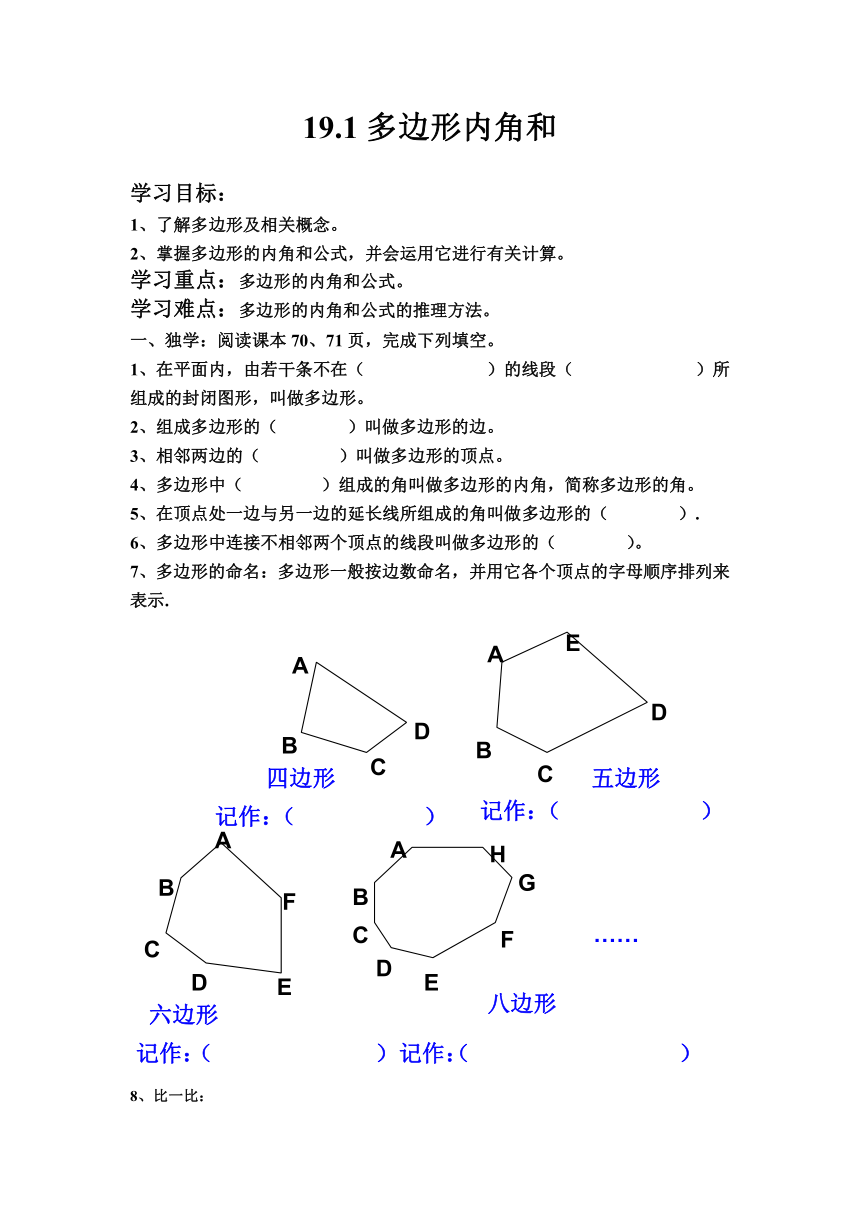
7、多边形的命名:多边形一般按边数命名,并用它各个顶点的字母顺序排列来表示.
(
四边形
五边形
六边形
八边形
……
A
B
D
C
B
A
D
C
F
E
D
C
B
A
E
A
H
G
F
E
D
C
B
记作:
(
)
记作:
(
)
记作:
(
)
记作:
(
)
)
8、比一比:
一个多边形,如果把它( )一边双向延长,其他各边都在延长所得直线的( ),这样的多边形就是( )。 我们所研究的多边形都指凸多边形。
二、合作探究。
(一)、探究四边形的内角和。
1、如右图①,四边形ABCD可分为( )个三角形,
它的内角和是:
2、如右图②,四边形ABCD可分为( )个三角形,
它的内角和是:
(二) 、探究五边形的内角和。
(三)归纳总结:按照第一种分割的做法来看
多边形边数 从一个顶点引出对角线数 图 形 分割成的三角形个数 多边形的内角和
4
5
6
... …… …… …… ……
n
定理:n边形的内角和等于 (n为不小于3的整数)
三、当堂训练,巩固基础.
1、①求一个八边形的内角和?②求一个十边形的内角和?
2、如果一个多边形的内角和是1440°,那么这是几边形?
3、四边形ABCD中,四个内角度数之比是1:2:3:4,求出四个内角的度数?
学习目标:
1、了解多边形及相关概念。
2、掌握多边形的内角和公式,并会运用它进行有关计算。
学习重点:多边形的内角和公式。
学习难点:多边形的内角和公式的推理方法。
一、独学:阅读课本70、71页,完成下列填空。
1、在平面内,由若干条不在( )的线段( )所组成的封闭图形,叫做多边形。
2、组成多边形的( )叫做多边形的边。
3、相邻两边的( )叫做多边形的顶点。
4、多边形中( )组成的角叫做多边形的内角,简称多边形的角。
5、在顶点处一边与另一边的延长线所组成的角叫做多边形的( ).
6、多边形中连接不相邻两个顶点的线段叫做多边形的( )。
7、多边形的命名:多边形一般按边数命名,并用它各个顶点的字母顺序排列来表示.
(
四边形
五边形
六边形
八边形
……
A
B
D
C
B
A
D
C
F
E
D
C
B
A
E
A
H
G
F
E
D
C
B
记作:
(
)
记作:
(
)
记作:
(
)
记作:
(
)
)
8、比一比:
一个多边形,如果把它( )一边双向延长,其他各边都在延长所得直线的( ),这样的多边形就是( )。 我们所研究的多边形都指凸多边形。
二、合作探究。
(一)、探究四边形的内角和。
1、如右图①,四边形ABCD可分为( )个三角形,
它的内角和是:
2、如右图②,四边形ABCD可分为( )个三角形,
它的内角和是:
(二) 、探究五边形的内角和。
(三)归纳总结:按照第一种分割的做法来看
多边形边数 从一个顶点引出对角线数 图 形 分割成的三角形个数 多边形的内角和
4
5
6
... …… …… …… ……
n
定理:n边形的内角和等于 (n为不小于3的整数)
三、当堂训练,巩固基础.
1、①求一个八边形的内角和?②求一个十边形的内角和?
2、如果一个多边形的内角和是1440°,那么这是几边形?
3、四边形ABCD中,四个内角度数之比是1:2:3:4,求出四个内角的度数?
