沪科版数学八年级下册 18.1 勾股定理教案
文档属性
| 名称 | 沪科版数学八年级下册 18.1 勾股定理教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 197.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 10:25:44 | ||
图片预览


文档简介
勾股定理
【教学目标】
知识技能:了解勾股定理的文化背景,体验勾股定理的探索过程.
数学思考:在勾股定理的探索过程中,发展合情推理能力,体会数形结合的思想.
解决问题:1.通过拼图活动,体验数学思维的严谨性,发展形象思维.
2.在探究活动中,学会与人合作并能与他人交流思维的过程和探究结果.
情感态度:1.通过对勾股定理历史的了解,感受数学文化,激发学习热情.
2.在探究活动中,体验解决问题方法的多样性,培养学生的合作交流意识和探索精神.
【教学重点与难点】 1、重点是探索和证明勾股定理.
2、难点是用拼图的方法证明勾股定理.
二、 教学过程:
(一)情景导入
国庆节前,为了更好观看阅兵式,小明妈妈买了一部42英寸(106厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有85厘米长和64厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
(二)小组交流,前置性研究,探索新知
相传两千五百年前,一次毕达哥拉斯去朋友家做客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
(
c
A B
)
数学家毕达哥拉斯的发现:
SA+SB=SC
设:直角三角形的三边长分别是a、b、c 猜想:两直角边a、b与斜边c 之间的关系?
SA+SB=SC
SA=a2 SB=b2 SC=c2
a2+b2=c2
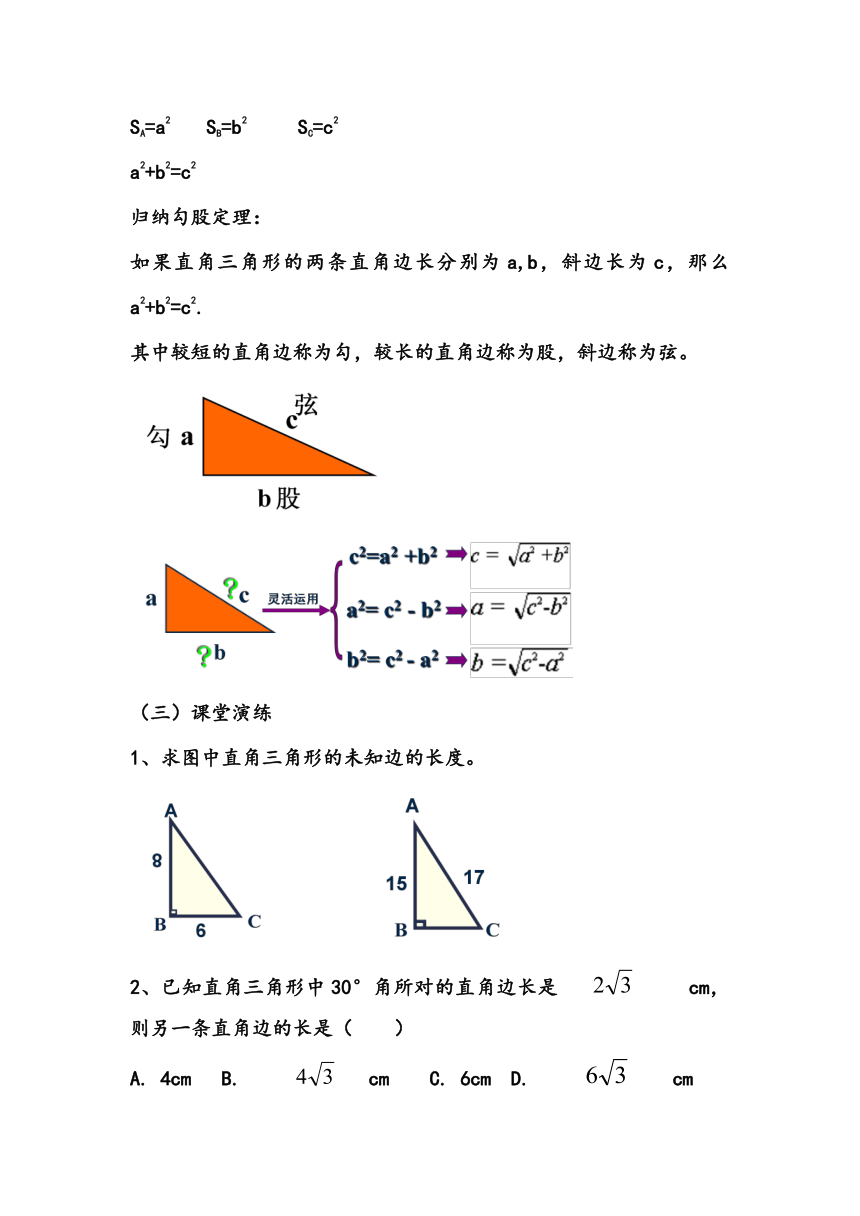
归纳勾股定理:
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
其中较短的直角边称为勾,较长的直角边称为股,斜边称为弦。
(三)课堂演练
1、求图中直角三角形的未知边的长度。
2、已知直角三角形中30°角所对的直角边长是 cm,则另一条直角边的长是( )
A. 4cm B. cm C. 6cm D. cm
例1 总统巧证勾股定理
美国第二十任总统伽菲尔德
3、 请利用此图象,证明勾股定理: a2+b2=c2
例2 如图,受台风莫拉克影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
(四)回头再看看
国庆节前,为了更好观看阅兵式,小明妈妈买了一部42英寸(106厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有85厘米长和64厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
(五)课堂小结
(1)运用勾股定理的条件是什么?
直角三角形才有勾股定理。
(2)勾股定理揭示了直角三角形的什么关系?
直角三角形中两直角边和斜边的数量关系。
(3)勾股定理的证明方法你学会了吗?
面积法。
(六)课堂作业:
1、求下列直角三角形中未知边的长:
2、如图所示,一棵大树在一次强烈台风中于离地面10米处折断倒下, 树顶落在离树根24米处.大树在折断之前高多少?
【教学目标】
知识技能:了解勾股定理的文化背景,体验勾股定理的探索过程.
数学思考:在勾股定理的探索过程中,发展合情推理能力,体会数形结合的思想.
解决问题:1.通过拼图活动,体验数学思维的严谨性,发展形象思维.
2.在探究活动中,学会与人合作并能与他人交流思维的过程和探究结果.
情感态度:1.通过对勾股定理历史的了解,感受数学文化,激发学习热情.
2.在探究活动中,体验解决问题方法的多样性,培养学生的合作交流意识和探索精神.
【教学重点与难点】 1、重点是探索和证明勾股定理.
2、难点是用拼图的方法证明勾股定理.
二、 教学过程:
(一)情景导入
国庆节前,为了更好观看阅兵式,小明妈妈买了一部42英寸(106厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有85厘米长和64厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
(二)小组交流,前置性研究,探索新知
相传两千五百年前,一次毕达哥拉斯去朋友家做客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
(
c
A B
)
数学家毕达哥拉斯的发现:
SA+SB=SC
设:直角三角形的三边长分别是a、b、c 猜想:两直角边a、b与斜边c 之间的关系?
SA+SB=SC
SA=a2 SB=b2 SC=c2
a2+b2=c2
归纳勾股定理:
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
其中较短的直角边称为勾,较长的直角边称为股,斜边称为弦。
(三)课堂演练
1、求图中直角三角形的未知边的长度。
2、已知直角三角形中30°角所对的直角边长是 cm,则另一条直角边的长是( )
A. 4cm B. cm C. 6cm D. cm
例1 总统巧证勾股定理
美国第二十任总统伽菲尔德
3、 请利用此图象,证明勾股定理: a2+b2=c2
例2 如图,受台风莫拉克影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
(四)回头再看看
国庆节前,为了更好观看阅兵式,小明妈妈买了一部42英寸(106厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有85厘米长和64厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
(五)课堂小结
(1)运用勾股定理的条件是什么?
直角三角形才有勾股定理。
(2)勾股定理揭示了直角三角形的什么关系?
直角三角形中两直角边和斜边的数量关系。
(3)勾股定理的证明方法你学会了吗?
面积法。
(六)课堂作业:
1、求下列直角三角形中未知边的长:
2、如图所示,一棵大树在一次强烈台风中于离地面10米处折断倒下, 树顶落在离树根24米处.大树在折断之前高多少?
