函数单调性

课件19张PPT。函数的单调性淮安市清河中学 数与形,本是相倚依
焉能分作两边飞
数无形时少直觉
形少数时难入微
数形结合百般好
隔离分家万事休
切莫忘,几何代数统一体
永远联系莫分离
—— 华罗庚
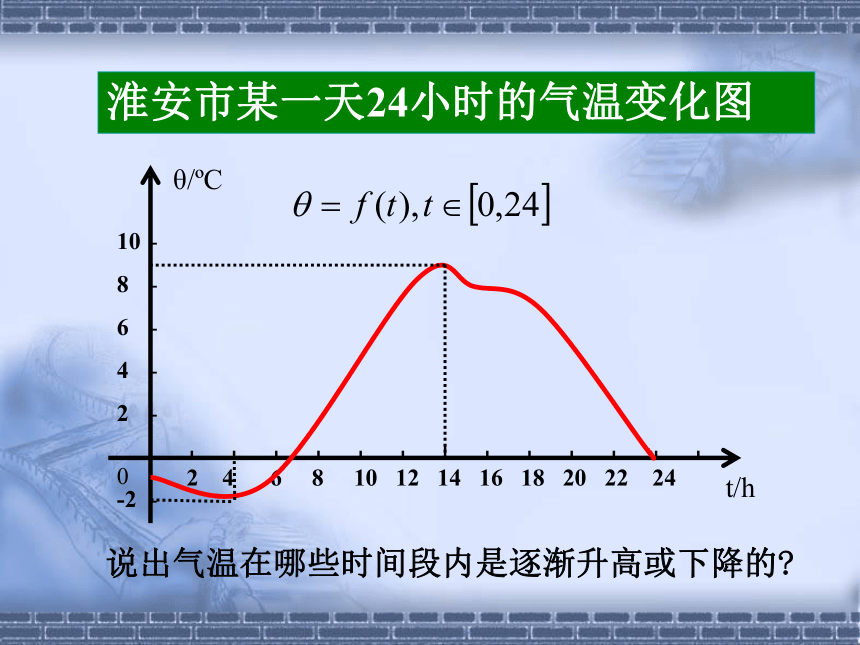
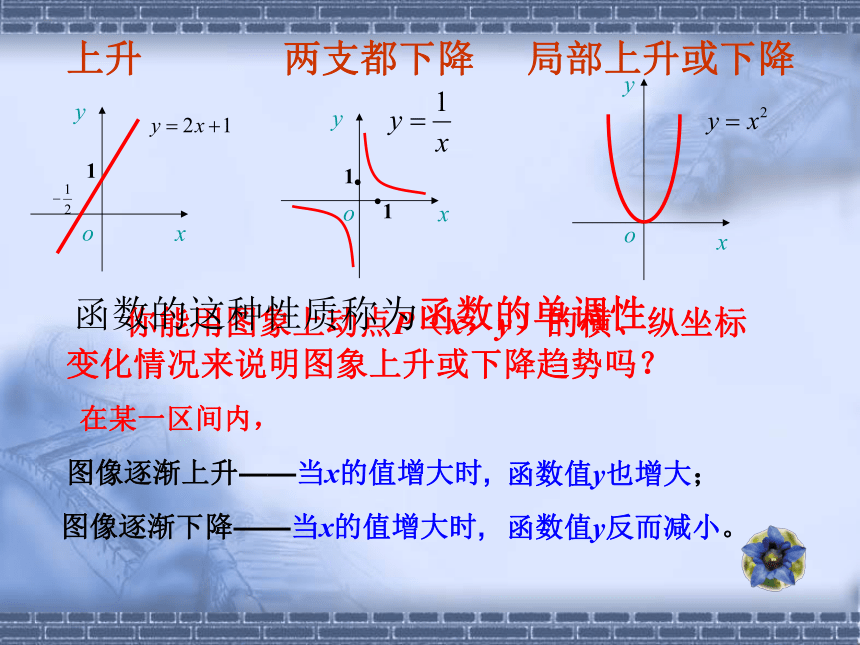
淮安市某一天24小时的气温变化图说出气温在哪些时间段内是逐渐升高或下降的? 你能用图象上动点P（x，y）的横、纵坐标变化情况来说明图象上升或下降趋势吗？图像逐渐上升——当x的值增大时,图像逐渐下降——当x的值增大时,函数的这种性质称为函数的单调性局部上升或下降两支都下降上升在某一区间内，函数值y也增大；函数值y反而减小。对区间I内 x1，x2 ，
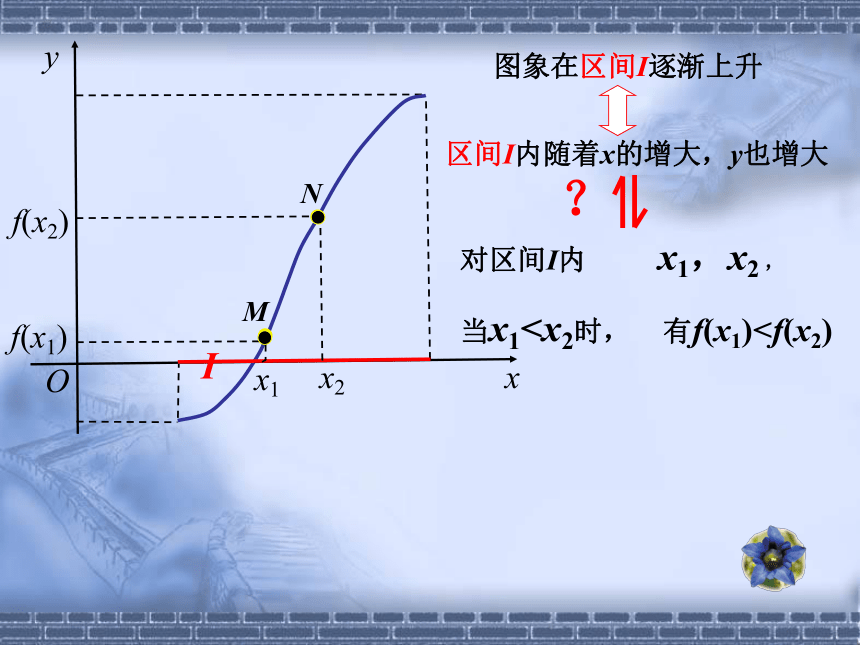
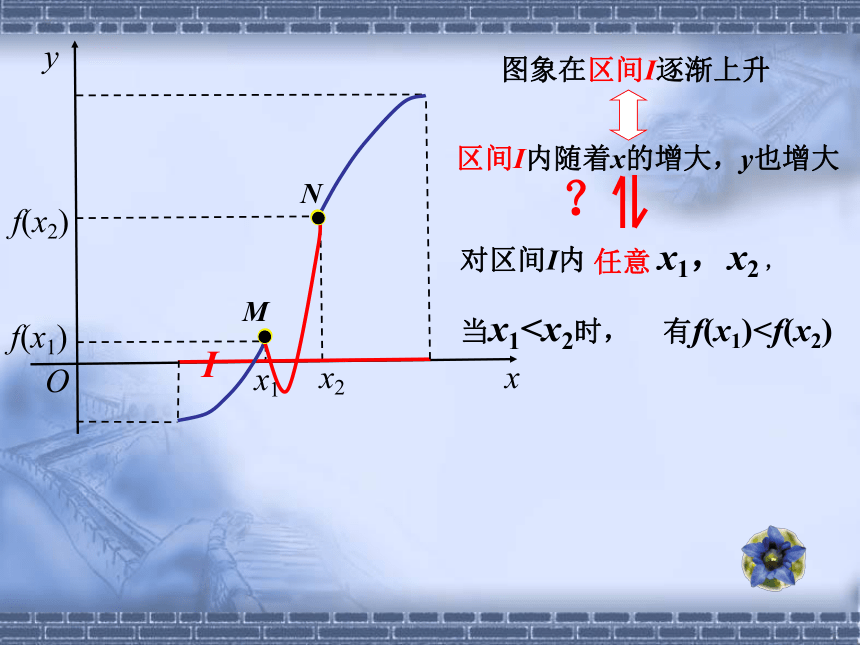
当x1当x1当x1MN任意两个自变量的值x1,x2，区间I内随着x的增大，y也增大图象在区间I逐渐上升I 那么就说在f(x)这个区间上是单调
减函数，I称为f(x)的单调 减 区间.类比单调增函数的研究方法定义单调减函数.x 如果对于属于定义域A内某个区间I上
的任意两个自变量的值x1,x2， 如果对于属于定义域A内某个区间I上
的任意两个自变量的值x1,x2， 那么就说在f(x)这个区间上是单调增 函数，I称为f(x)的单调 区间.增当x1单调区间 如果函数 y =f(x)在区间I是单调增函数或单调减函数，那么就说函数 y =f(x)在区间I上具有单调性。
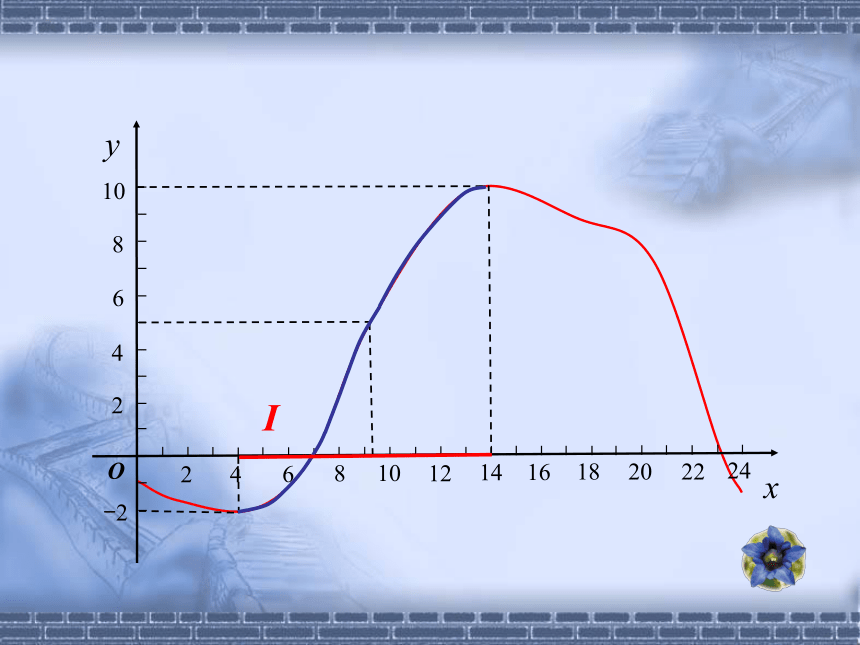
在单调区间上，增函数的图象是 的，减函数的图象是 的。上升下降注意：（1）函数单调性是针对某个区间而言的，是一个局部性质;该函数的单调增区间是________ ,单调减区间是______________.[4,14][0,4],[14,24]能否说:该函数是增函数?不能该函数在区间[4,14]上是增函数。（1）函数单调性是针对某个区间而言的，是一个局部性质;注意：判断2：定义在R上的函数 f (x)满足 f (2)> f(1)，则函数 f (x)在R上是增函数.（2） x 1, x 2 取值的任意性.判断1： f (x)是R上的增函数,则 f (2)> f(1).判断3：f (x)是R上的减函数,且 f (a)> f(b),则a2. 作差f(x1)－f(x2)；
3. 变形（通分，因式分解和配方等）；
4. 定号（即判断差f(x1)－f(x2)的正负）；
5. 下结论。证明函数单调性的主要步骤:形少数时难入微练一练 小结
1.函数单调性的定义中有哪些关键点？
2.判断函数单调性有哪些常用方法？
3.你学会了哪些数学思想方法？思考