5.2 平行线及其判定 同步练习(含解析)
文档属性
| 名称 | 5.2 平行线及其判定 同步练习(含解析) | 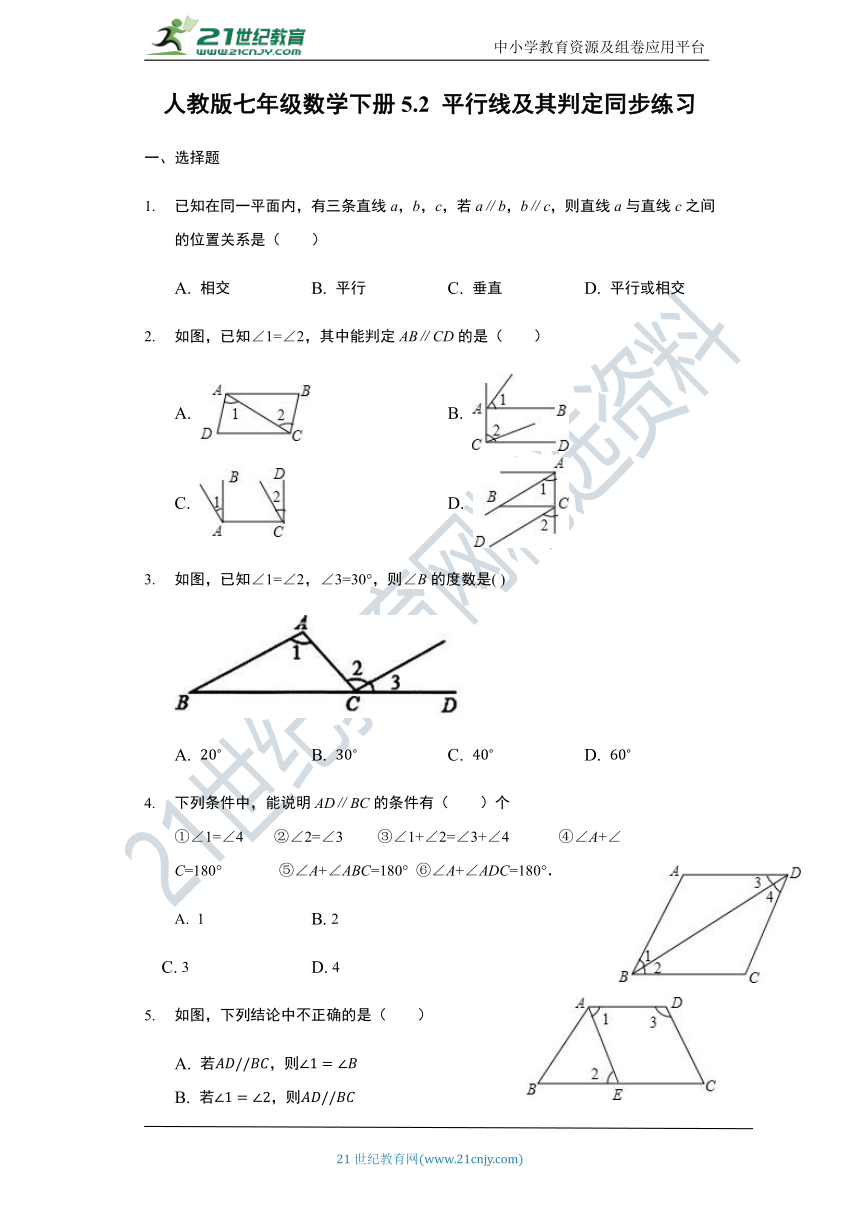 | |
| 格式 | docx | ||
| 文件大小 | 240.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 15:00:08 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版七年级数学下册5.2 平行线及其判定同步练习
一、选择题
已知在同一平面内,有三条直线a,b,c,若a∥b,b∥c,则直线a与直线c之间的位置关系是( )
A. 相交 B. 平行 C. 垂直 D. 平行或相交
如图,已知∠1=∠2,其中能判定AB∥CD的是( )
A. B.
C. D.
如图,已知∠1=∠2,∠3=30°,则∠B的度数是( )
A. B. C. D.
下列条件中,能说明AD∥BC的条件有( )个
①∠1=∠4 ②∠2=∠3 ③∠1+∠2=∠3+∠4 ④∠A+∠C=180° ⑤∠A+∠ABC=180° ⑥∠A+∠ADC=180°.
1 B. 2
C. 3 D. 4
如图,下列结论中不正确的是( )
A. 若,则
B. 若,则
C. 若,则
D. 若,则
如图,在条件:①∠5=∠6,②∠7=∠2,③∠3+∠8=180°,④∠3=∠2,⑤∠4+∠1=180°中,能判定a∥b的条件有( )
A. 4个
B. 3个
C. 2个
D. 1个
如图,已知∠2=100°,要使AB∥CD,则须具备另一个条件( )
A.
B.
C.
D.
以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
A. 如图1,展开后测得
B. 如图2,展开后测得且
C. 如图3,测得
D. 如图4,展开后再沿CD折叠,两条折痕的交点为O,测得,
二、填空题
如图,∠ACD=∠A,∠BCF=∠B,则∠A+∠B+∠ACB等于______ .
如图,若∠1+∠2=180°,∠3=110°,则∠4=______.
若AB∥CD,AB∥EF,则______ ∥ ______ ,理由是______ .
如图,点E在AC的延长线上,对于给出的四个条件:
(1)∠3=∠4;(2)∠1=∠2;(3)∠A=∠DCE;(4)∠D+∠ABD=180°.
能判断AB∥CD的有______个.
如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒20°的速度沿顺时针方向旋转一周,在旋转的过程中,在第______秒时,边CD恰好与边AB平行.
三、计算题
已知:如图,AB∥CD,∠1=∠2,∠3=∠4.
(1)求证:AD∥BE;
(2)若∠B=∠3=2∠2,求∠D的度数.
如图,已知∠1=52°,∠2=128°,∠C=∠D,探索∠A与∠F的数量关系,并说明理由.
如图,在△ABC中,AD⊥BC,垂足为D,点E在AB上,EF⊥BC,垂足为F.
(1)AD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠BAC的度数.
答案
1.【答案】B
【解析】
解:∵在同一平面内,直线a∥b,直线b∥c,
∴直线c与直线a的位置关系是:a∥c.
故选B.
2.【答案】D
解:A、∵∠1=∠2,
∴AD∥BC(内错角相等,两直线平行);
B、∵∠1=∠2,∠1、∠2不是同位角和内错角,
∴不能得出两直线平行;
C、∠1=∠2,∠1、∠2不是同位角和内错角,
∴不能得出两直线平行;
D、∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行).
故选D.
3.【答案】B
【解析】
解:如图,
∵∠1=∠2,
∴AB∥CE,
∴∠B=∠3.
又∵∠3=30°,
∴∠B=30°.
故选B.
4.【答案】B
【解析】
解:①∠1=∠4,可得AB∥DC,错误;②∠2=∠3,可得AD∥BC,正确;③∠1+∠2=∠3+∠4,不能判断AD∥BC,错误;④∠A+∠C=180°,不能判断AD∥BC,错误;⑤∠A+∠ABC=180°,可得AD∥BC,正确;⑥∠A+∠ADC=180°,可得AB∥DC,错误;
故选:B.
5.【答案】A
【解析】
解:∵AD∥BC,
∴∠1=∠2,选项A不正确;
∵∠1=∠2,
∴AD∥BC,选项B正确;
∵∠2=∠C,
∴AE∥CD,选项C正确;
∵AE∥CD,
∴∠1+∠3=180°,选项D正确;
故选:A.
6.【答案】A
【解析】
解:∵∠5=∠6,
∴a∥b,∴①正确;
∵∠7=∠2,
∴a∥b,∴②正确;
∵∠2=∠8=180°,∠3+∠8=180°,
∴∠3+∠2=180°,
∴a∥b,∴③正确;
∵∠4=∠6,1=∠7,∠4+∠1=180°,
∴∠6+∠7=180°,
∴a∥b,∴⑤正确;
而④不能推出a∥b;∴④错误;
能判断a∥b的条件有①②③⑤,
故选A.
7.【答案】D
【解析】
解:∵∠2=100°,
∴根据平行线的判定可知,当∠4=100°,或∠3=100°,或∠1=80°时,AB∥CD.
故选(D)
8.【答案】C
【解析】
解:A、∠1=∠2,根据内错角相等,两直线平行进行判定,故正确;
B、∵∠1=∠2且∠3=∠4,由图可知∠1+∠2=180°,∠3+∠4=180°,
∴∠1=∠2=∠3=∠4=90°,
∴a∥b(内错角相等,两直线平行),
故正确;
C、测得∠1=∠2,
∵∠1与∠2即不是内错角也不是同位角,
∴不一定能判定两直线平行,故错误;
D、在△AOC和△BOD中,
,
∴△AOC≌△BOD,
∴∠CAO=∠DBO,
∴a∥b(内错角相等,两直线平行),
故正确.
故选:C.
9.【答案】180°
【解析】
解:∵∠ACD=∠A,∠BCF=∠B,∠DCF=∠ACD+∠ACB+∠BCF=180°,
∴∠A+∠B+∠ACB=∠ACD+∠ACB+∠BCF=180°.
故答案为:180°.
10.【答案】110°
【解析】
解:如图,∵∠1+∠2=180°,
∴a∥b,
∴∠3=∠4,
又∵∠3=110°,
∴∠4=110°.
故答案为:110°.
11.【答案】CD;EF;平行于同一条直线的两条直线互相平行.
【解析】
解:∵AB∥CD,AB∥EF,
∴CD∥EF,
理由是:如果两条直线都和第三条直线平行,那么这两条直线平行,
故答案为平行于同一条直线的两条直线互相平行.
12.【答案】3
【解析】
解:(1)如果∠3=∠4,那么AC∥BD,故(1)错误;
(2)∠1=∠2,那么AB∥CD;内错角相等,两直线平行,故(2)正确;
(3)∠A=∠DCE,那么AB∥CD;同位角相等,两直线平行,故(3)正确;
(4)∠D+∠ABD=180°,那么AB∥CD;同旁内角互补,两直线平行,故(4)正确.
即正确的有(2)(3)(4).
故答案为:3.
13.【答案】5或14
【解析】
解:如图1,△COD绕点O顺时针旋转得到△C′OD′,C′D′交OB于E,则∠C′OD′=∠COD=90°,∠OC′D=∠C=60°,
当∠OEC′=∠B=40°时,C′D′∥AB,
∴∠C′OC=∠OEC′+∠OC′E=40°+60°=100°,
∴△COD绕点O顺时针旋转100°得到△C′OD′所需时间为=5(秒);
如图2,△COD绕点O顺时针旋转得到△C″OD″,C″D″交直线OB于F,则∠C″OD″=∠COD=90°,∠OC″D=∠C=60°,
当∠OFC″=∠B=40°时,C″D″∥AB,
∴∠C″OC=180°-∠OFC″+∠OC′F=180°-40°-60°=80°,
而360°-80°=280°,
∴△COD绕点O顺时针旋280°得到△C″OD″所需时间为=14(秒);
综上所述,在旋转的过程中,在第5秒或14秒时,边CD恰好与边AB平行.
讨论:如图1,△COD绕点O顺时针旋转得到△C′OD′,C′D′交OB于E,了;一平行线的判定,当∠OEC′=∠B=40°时,C′D′∥AB,则根据三角形外角性质计算出∠C′OC=100°,从而可计算出此时△COD绕点O顺时针旋转100°得到△C′OD′所需时间;如图2,△COD绕点O顺时针旋转得到△C″OD″,C″D″交直线OB于F,利用平行线的判定得当∠OFC″=∠B=40°时,C″D″∥AB,根据三角形内角和计算出∠C″OC=80°,则△COD绕点O顺时针旋280°得到△C″OD″,然后计算此时旋转的时间.
14.【答案】(1)证明:∵AB∥CD,
∴∠1=∠ACD,
∵∠BCD=∠4+∠E,
∵∠3=∠4,
∴∠1=∠E,
∵∠1=∠2,
∴∠2=∠E,
∴AD∥BE;
(2)解:∵∠B=∠3=2∠2,∠1=∠2,
∴∠B=∠3=2∠1,
∵∠B+∠3+∠1=180°,
即2∠1+2∠1+∠1=180°,解得∠1=36°,
∴∠B=2∠1=72°,
∵AB∥CD,
∴∠DCE=∠B=72°,
∵AD∥BE,
∴∠D=∠DCE=72°.
15.【答案】解:结论:∠A=∠F,理由为:
证明:∵∠1=52°,∠2=128°,
∴∠1+∠2=180°,
∴BD∥CE,
∴∠ABD=∠C,
∵∠C=∠D,
∴∠ABD=∠D,
∴AC∥DF,
∴∠A=∠F.
16.【答案】解:(1)AD与EF平行.理由如下:
∵AD⊥BC,EF⊥BC,
∴AD∥EF;
(2)∵AD∥EF,
∴∠2=∠BAD,
而∠1=∠2,
∴∠1=∠BAD,
∴AB∥DG,
∴∠BAC=∠3=115°.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版七年级数学下册5.2 平行线及其判定同步练习
一、选择题
已知在同一平面内,有三条直线a,b,c,若a∥b,b∥c,则直线a与直线c之间的位置关系是( )
A. 相交 B. 平行 C. 垂直 D. 平行或相交
如图,已知∠1=∠2,其中能判定AB∥CD的是( )
A. B.
C. D.
如图,已知∠1=∠2,∠3=30°,则∠B的度数是( )
A. B. C. D.
下列条件中,能说明AD∥BC的条件有( )个
①∠1=∠4 ②∠2=∠3 ③∠1+∠2=∠3+∠4 ④∠A+∠C=180° ⑤∠A+∠ABC=180° ⑥∠A+∠ADC=180°.
1 B. 2
C. 3 D. 4
如图,下列结论中不正确的是( )
A. 若,则
B. 若,则
C. 若,则
D. 若,则
如图,在条件:①∠5=∠6,②∠7=∠2,③∠3+∠8=180°,④∠3=∠2,⑤∠4+∠1=180°中,能判定a∥b的条件有( )
A. 4个
B. 3个
C. 2个
D. 1个
如图,已知∠2=100°,要使AB∥CD,则须具备另一个条件( )
A.
B.
C.
D.
以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
A. 如图1,展开后测得
B. 如图2,展开后测得且
C. 如图3,测得
D. 如图4,展开后再沿CD折叠,两条折痕的交点为O,测得,
二、填空题
如图,∠ACD=∠A,∠BCF=∠B,则∠A+∠B+∠ACB等于______ .
如图,若∠1+∠2=180°,∠3=110°,则∠4=______.
若AB∥CD,AB∥EF,则______ ∥ ______ ,理由是______ .
如图,点E在AC的延长线上,对于给出的四个条件:
(1)∠3=∠4;(2)∠1=∠2;(3)∠A=∠DCE;(4)∠D+∠ABD=180°.
能判断AB∥CD的有______个.
如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒20°的速度沿顺时针方向旋转一周,在旋转的过程中,在第______秒时,边CD恰好与边AB平行.
三、计算题
已知:如图,AB∥CD,∠1=∠2,∠3=∠4.
(1)求证:AD∥BE;
(2)若∠B=∠3=2∠2,求∠D的度数.
如图,已知∠1=52°,∠2=128°,∠C=∠D,探索∠A与∠F的数量关系,并说明理由.
如图,在△ABC中,AD⊥BC,垂足为D,点E在AB上,EF⊥BC,垂足为F.
(1)AD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠BAC的度数.
答案
1.【答案】B
【解析】
解:∵在同一平面内,直线a∥b,直线b∥c,
∴直线c与直线a的位置关系是:a∥c.
故选B.
2.【答案】D
解:A、∵∠1=∠2,
∴AD∥BC(内错角相等,两直线平行);
B、∵∠1=∠2,∠1、∠2不是同位角和内错角,
∴不能得出两直线平行;
C、∠1=∠2,∠1、∠2不是同位角和内错角,
∴不能得出两直线平行;
D、∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行).
故选D.
3.【答案】B
【解析】
解:如图,
∵∠1=∠2,
∴AB∥CE,
∴∠B=∠3.
又∵∠3=30°,
∴∠B=30°.
故选B.
4.【答案】B
【解析】
解:①∠1=∠4,可得AB∥DC,错误;②∠2=∠3,可得AD∥BC,正确;③∠1+∠2=∠3+∠4,不能判断AD∥BC,错误;④∠A+∠C=180°,不能判断AD∥BC,错误;⑤∠A+∠ABC=180°,可得AD∥BC,正确;⑥∠A+∠ADC=180°,可得AB∥DC,错误;
故选:B.
5.【答案】A
【解析】
解:∵AD∥BC,
∴∠1=∠2,选项A不正确;
∵∠1=∠2,
∴AD∥BC,选项B正确;
∵∠2=∠C,
∴AE∥CD,选项C正确;
∵AE∥CD,
∴∠1+∠3=180°,选项D正确;
故选:A.
6.【答案】A
【解析】
解:∵∠5=∠6,
∴a∥b,∴①正确;
∵∠7=∠2,
∴a∥b,∴②正确;
∵∠2=∠8=180°,∠3+∠8=180°,
∴∠3+∠2=180°,
∴a∥b,∴③正确;
∵∠4=∠6,1=∠7,∠4+∠1=180°,
∴∠6+∠7=180°,
∴a∥b,∴⑤正确;
而④不能推出a∥b;∴④错误;
能判断a∥b的条件有①②③⑤,
故选A.
7.【答案】D
【解析】
解:∵∠2=100°,
∴根据平行线的判定可知,当∠4=100°,或∠3=100°,或∠1=80°时,AB∥CD.
故选(D)
8.【答案】C
【解析】
解:A、∠1=∠2,根据内错角相等,两直线平行进行判定,故正确;
B、∵∠1=∠2且∠3=∠4,由图可知∠1+∠2=180°,∠3+∠4=180°,
∴∠1=∠2=∠3=∠4=90°,
∴a∥b(内错角相等,两直线平行),
故正确;
C、测得∠1=∠2,
∵∠1与∠2即不是内错角也不是同位角,
∴不一定能判定两直线平行,故错误;
D、在△AOC和△BOD中,
,
∴△AOC≌△BOD,
∴∠CAO=∠DBO,
∴a∥b(内错角相等,两直线平行),
故正确.
故选:C.
9.【答案】180°
【解析】
解:∵∠ACD=∠A,∠BCF=∠B,∠DCF=∠ACD+∠ACB+∠BCF=180°,
∴∠A+∠B+∠ACB=∠ACD+∠ACB+∠BCF=180°.
故答案为:180°.
10.【答案】110°
【解析】
解:如图,∵∠1+∠2=180°,
∴a∥b,
∴∠3=∠4,
又∵∠3=110°,
∴∠4=110°.
故答案为:110°.
11.【答案】CD;EF;平行于同一条直线的两条直线互相平行.
【解析】
解:∵AB∥CD,AB∥EF,
∴CD∥EF,
理由是:如果两条直线都和第三条直线平行,那么这两条直线平行,
故答案为平行于同一条直线的两条直线互相平行.
12.【答案】3
【解析】
解:(1)如果∠3=∠4,那么AC∥BD,故(1)错误;
(2)∠1=∠2,那么AB∥CD;内错角相等,两直线平行,故(2)正确;
(3)∠A=∠DCE,那么AB∥CD;同位角相等,两直线平行,故(3)正确;
(4)∠D+∠ABD=180°,那么AB∥CD;同旁内角互补,两直线平行,故(4)正确.
即正确的有(2)(3)(4).
故答案为:3.
13.【答案】5或14
【解析】
解:如图1,△COD绕点O顺时针旋转得到△C′OD′,C′D′交OB于E,则∠C′OD′=∠COD=90°,∠OC′D=∠C=60°,
当∠OEC′=∠B=40°时,C′D′∥AB,
∴∠C′OC=∠OEC′+∠OC′E=40°+60°=100°,
∴△COD绕点O顺时针旋转100°得到△C′OD′所需时间为=5(秒);
如图2,△COD绕点O顺时针旋转得到△C″OD″,C″D″交直线OB于F,则∠C″OD″=∠COD=90°,∠OC″D=∠C=60°,
当∠OFC″=∠B=40°时,C″D″∥AB,
∴∠C″OC=180°-∠OFC″+∠OC′F=180°-40°-60°=80°,
而360°-80°=280°,
∴△COD绕点O顺时针旋280°得到△C″OD″所需时间为=14(秒);
综上所述,在旋转的过程中,在第5秒或14秒时,边CD恰好与边AB平行.
讨论:如图1,△COD绕点O顺时针旋转得到△C′OD′,C′D′交OB于E,了;一平行线的判定,当∠OEC′=∠B=40°时,C′D′∥AB,则根据三角形外角性质计算出∠C′OC=100°,从而可计算出此时△COD绕点O顺时针旋转100°得到△C′OD′所需时间;如图2,△COD绕点O顺时针旋转得到△C″OD″,C″D″交直线OB于F,利用平行线的判定得当∠OFC″=∠B=40°时,C″D″∥AB,根据三角形内角和计算出∠C″OC=80°,则△COD绕点O顺时针旋280°得到△C″OD″,然后计算此时旋转的时间.
14.【答案】(1)证明:∵AB∥CD,
∴∠1=∠ACD,
∵∠BCD=∠4+∠E,
∵∠3=∠4,
∴∠1=∠E,
∵∠1=∠2,
∴∠2=∠E,
∴AD∥BE;
(2)解:∵∠B=∠3=2∠2,∠1=∠2,
∴∠B=∠3=2∠1,
∵∠B+∠3+∠1=180°,
即2∠1+2∠1+∠1=180°,解得∠1=36°,
∴∠B=2∠1=72°,
∵AB∥CD,
∴∠DCE=∠B=72°,
∵AD∥BE,
∴∠D=∠DCE=72°.
15.【答案】解:结论:∠A=∠F,理由为:
证明:∵∠1=52°,∠2=128°,
∴∠1+∠2=180°,
∴BD∥CE,
∴∠ABD=∠C,
∵∠C=∠D,
∴∠ABD=∠D,
∴AC∥DF,
∴∠A=∠F.
16.【答案】解:(1)AD与EF平行.理由如下:
∵AD⊥BC,EF⊥BC,
∴AD∥EF;
(2)∵AD∥EF,
∴∠2=∠BAD,
而∠1=∠2,
∴∠1=∠BAD,
∴AB∥DG,
∴∠BAC=∠3=115°.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
