高中数学 1.2.1 排列 课件(新人教A版-选修2-3)
文档属性
| 名称 | 高中数学 1.2.1 排列 课件(新人教A版-选修2-3) |

|
|
| 格式 | zip | ||
| 文件大小 | 102.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-07 00:00:00 | ||
图片预览






文档简介
课件17张PPT。新课标人教版课件系列《高中数学》
选修2-31.2.1《排列》教学目标 理解排列、排列数的概念,了解排列数公式的推导
教学重点:
理解排列、排列数的概念,了解排列数公式的推导选修2-3 1.2 排 列第一课时分类计数原理(加法原理)?
完成一件事,有n类办法,在第1类办法中有m1 种不同的方法,在第2类办法中有m2 种不同的方法,…,在第n 类办法中有mn 种不同的方法,那么完成这件事共有:
种不同的方法.分步计数原理(乘法原理)完成一件事,需要分成n 个步骤,做第1步有m1 种不同的方法,做第2步有m2 种不同的方法,…,做第n步有mn 种不同的方法,那么完成这件事共有:
种不同的方法.分类计数原理与“分类”有关,各种方法相互独立,用其中任何一种方法都可以完成这件事;
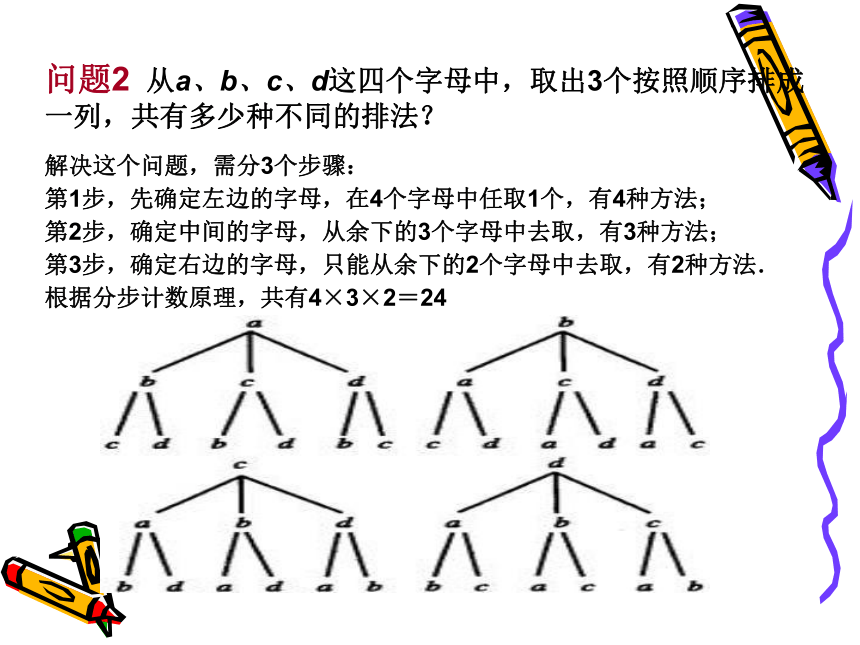
分步计数原理与“分步”有关,各个步骤相互依存,只有各个步骤都完成了,这件事才算完成.问题1? 从甲、乙、丙3名同学中选出2名参加某天的一项活动,其中1名同学参加上午的活动,1名同学参加下午的活动,有多少种不同的方法? 我们把上面问题中被取的对象叫做元素.于是所提出的问题就是从3个不同的元素中任取2个,按照一定的顺序排成一列,求一共有多少种不同的排法. 问题2? 从a、b、c、d这四个字母中,取出3个按照顺序排成一列,共有多少种不同的排法? 解决这个问题,需分3个步骤:
第1步,先确定左边的字母,在4个字母中任取1个,有4种方法;
第2步,确定中间的字母,从余下的3个字母中去取,有3种方法;
第3步,确定右边的字母,只能从余下的2个字母中去取,有2种方法.
根据分步计数原理,共有4×3×2=24 一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列. 注意:
1.我们所研究的排列问题,是不同元素的排列,这里既没有重复元素,也没有重复抽取相同的元素.3.根据排列的定义,两个排列相同,当且仅当这两个排列的元素完全相同,而且元素的排列顺序也完全相同.也就是说,如果两个排列所含的元素不完全一样,那么就可以肯定是不同的排列;如果两个排列所含的元素完全一样,但摆的顺序不同,那么也是不同的排列. 【总结提炼】
排列问题,是取出m个元素后,还要按一定的顺序排成一列,取出同样的m个元素,只要排列顺序不同,就视为完成这件事的两种不同的方法(两个不同的排列).
由排列的定义可知,排列与元素的顺序有关,也就是说与位置有关的问题才能归结为排列问题.当元素较少时,可以根据排列的意义写出所有的排列.练习2.写出从5个元素a,b,c,d,e中任取2个元素的所有排列. 解决办法是先画“树形图”,再由此写出所有的排列,共20个. 若把这题改为:写出从5个元素.a,b,c,d,e中任取4个元素的所有排列,结果如何呢?方法仍然照用,但数字将更大,写起来更“啰嗦”.练习1.在A、B、C、D四位候选人中,选举正、副班长各一人,共有几种不同的选法?写出所有可能的选举结果.AB? AC? AD? BC? BD? CD BA? CA? DA? CB? DB? DC 研究一个排列问题,往往只需知道所有排列的个数而无需一一写出所有的排列,那么能否不通过一一写出所有的排列而直接“得”出所有排列的个数呢?这一节课我们将来共同探讨这个问题:排列数及其公式. 1.排列数的定义
从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,记作 .注意区别“一个排列”与“排列数”的不同:
“一个排列”是指“从n个不同元素中,任取m个元素按照一定的顺序排成一列”,不是数;
“排列数”是指“从n个不同元素中取出m个元素的所有排列的个数”,是一个数.因此符号只代表排列数,而不表示具体的排列. 2.排列数公式 这里m、n 且m<n,这个公式叫做排列数公式.它有以下三个特点:
(1)第一个因数是n,后面每一个因数比它前面一个因数少1.
(2)最后一个因数是n-m+1.
(3)共有m个因数.正整数1到n的连乘积,叫做n的阶乘,用n! 表示。当m=n时例1. 计算
(1) ? (2) ? (3) 解:(1)
(2)
(3) 规定0!=1例2.解方程。 解:原方程可化为2x(2x-1)(2x-2)=100x(x-1)
∵x≠0,x≠1 ∴?2x-1=25
解得x=13 经检验x=13 是原方程的根。 例3.证明: 。 证明:右边1.全排列数(阶乘)
2.阶乘变形 例3:求证:1!+2·2!+3·3!+…+n·n!=(n+1)!-1分析:n·n!=(n+1)!-n!再见
选修2-31.2.1《排列》教学目标 理解排列、排列数的概念,了解排列数公式的推导
教学重点:
理解排列、排列数的概念,了解排列数公式的推导选修2-3 1.2 排 列第一课时分类计数原理(加法原理)?
完成一件事,有n类办法,在第1类办法中有m1 种不同的方法,在第2类办法中有m2 种不同的方法,…,在第n 类办法中有mn 种不同的方法,那么完成这件事共有:
种不同的方法.分步计数原理(乘法原理)完成一件事,需要分成n 个步骤,做第1步有m1 种不同的方法,做第2步有m2 种不同的方法,…,做第n步有mn 种不同的方法,那么完成这件事共有:
种不同的方法.分类计数原理与“分类”有关,各种方法相互独立,用其中任何一种方法都可以完成这件事;
分步计数原理与“分步”有关,各个步骤相互依存,只有各个步骤都完成了,这件事才算完成.问题1? 从甲、乙、丙3名同学中选出2名参加某天的一项活动,其中1名同学参加上午的活动,1名同学参加下午的活动,有多少种不同的方法? 我们把上面问题中被取的对象叫做元素.于是所提出的问题就是从3个不同的元素中任取2个,按照一定的顺序排成一列,求一共有多少种不同的排法. 问题2? 从a、b、c、d这四个字母中,取出3个按照顺序排成一列,共有多少种不同的排法? 解决这个问题,需分3个步骤:
第1步,先确定左边的字母,在4个字母中任取1个,有4种方法;
第2步,确定中间的字母,从余下的3个字母中去取,有3种方法;
第3步,确定右边的字母,只能从余下的2个字母中去取,有2种方法.
根据分步计数原理,共有4×3×2=24 一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列. 注意:
1.我们所研究的排列问题,是不同元素的排列,这里既没有重复元素,也没有重复抽取相同的元素.3.根据排列的定义,两个排列相同,当且仅当这两个排列的元素完全相同,而且元素的排列顺序也完全相同.也就是说,如果两个排列所含的元素不完全一样,那么就可以肯定是不同的排列;如果两个排列所含的元素完全一样,但摆的顺序不同,那么也是不同的排列. 【总结提炼】
排列问题,是取出m个元素后,还要按一定的顺序排成一列,取出同样的m个元素,只要排列顺序不同,就视为完成这件事的两种不同的方法(两个不同的排列).
由排列的定义可知,排列与元素的顺序有关,也就是说与位置有关的问题才能归结为排列问题.当元素较少时,可以根据排列的意义写出所有的排列.练习2.写出从5个元素a,b,c,d,e中任取2个元素的所有排列. 解决办法是先画“树形图”,再由此写出所有的排列,共20个. 若把这题改为:写出从5个元素.a,b,c,d,e中任取4个元素的所有排列,结果如何呢?方法仍然照用,但数字将更大,写起来更“啰嗦”.练习1.在A、B、C、D四位候选人中,选举正、副班长各一人,共有几种不同的选法?写出所有可能的选举结果.AB? AC? AD? BC? BD? CD BA? CA? DA? CB? DB? DC 研究一个排列问题,往往只需知道所有排列的个数而无需一一写出所有的排列,那么能否不通过一一写出所有的排列而直接“得”出所有排列的个数呢?这一节课我们将来共同探讨这个问题:排列数及其公式. 1.排列数的定义
从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,记作 .注意区别“一个排列”与“排列数”的不同:
“一个排列”是指“从n个不同元素中,任取m个元素按照一定的顺序排成一列”,不是数;
“排列数”是指“从n个不同元素中取出m个元素的所有排列的个数”,是一个数.因此符号只代表排列数,而不表示具体的排列. 2.排列数公式 这里m、n 且m<n,这个公式叫做排列数公式.它有以下三个特点:
(1)第一个因数是n,后面每一个因数比它前面一个因数少1.
(2)最后一个因数是n-m+1.
(3)共有m个因数.正整数1到n的连乘积,叫做n的阶乘,用n! 表示。当m=n时例1. 计算
(1) ? (2) ? (3) 解:(1)
(2)
(3) 规定0!=1例2.解方程。 解:原方程可化为2x(2x-1)(2x-2)=100x(x-1)
∵x≠0,x≠1 ∴?2x-1=25
解得x=13 经检验x=13 是原方程的根。 例3.证明: 。 证明:右边1.全排列数(阶乘)
2.阶乘变形 例3:求证:1!+2·2!+3·3!+…+n·n!=(n+1)!-1分析:n·n!=(n+1)!-n!再见
