8.4三元一次方程组的解法 专项练习(含解析)
文档属性
| 名称 | 8.4三元一次方程组的解法 专项练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 76.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 15:27:16 | ||
图片预览


文档简介
七年级数学下册三元一次方程组的解法专项练习
学校: 姓名: 班级: 考号:
评卷人 得分 一、选择题
1. 下列各方程组中,是三元一次方程组的是( )
①②
③④
A. ①②④ B. ①②③ C. ②③ D. ①②③④
2. 解方程组若要使运算简便,消元的方法应选( )
A. 消去x B. 消去y C. 消去z D. 以上说法都不对
3. 方程组的解是( )
A. B. C. D.
4. 已知方程组则x+y+z的值为( )
A. 6 B. -6 C. 5 D. -5
5. 某校团委与社区联合举办“保护地球,人人有责”活动,选派20名学生分三组到120个店铺发传单,若第一,二,三小组每人分别负责8,6,5个店铺,且每组至少有两人,则学生分组方案有( )
A. 6种 B. 5种 C. 4种 D. 3种
评卷人 得分 二、填空题
6. 若x+2y+3z=10,4x+3y+2z=15,则x+y+z的值是 .
7. 已知2ay+5b3x+ycz-x与-4a2xb5cy是同类项,则x-y+z的值为 .
8. 在y=ax2+bx+c中,当x=1时,y=0;当x=2时,y=4;当x=3时,y=10,则当x=4时,y= .
9. 若|a+b-3|+(5a-b-c)2+|2c+b-8|=0,则a= ,b= ,c= .
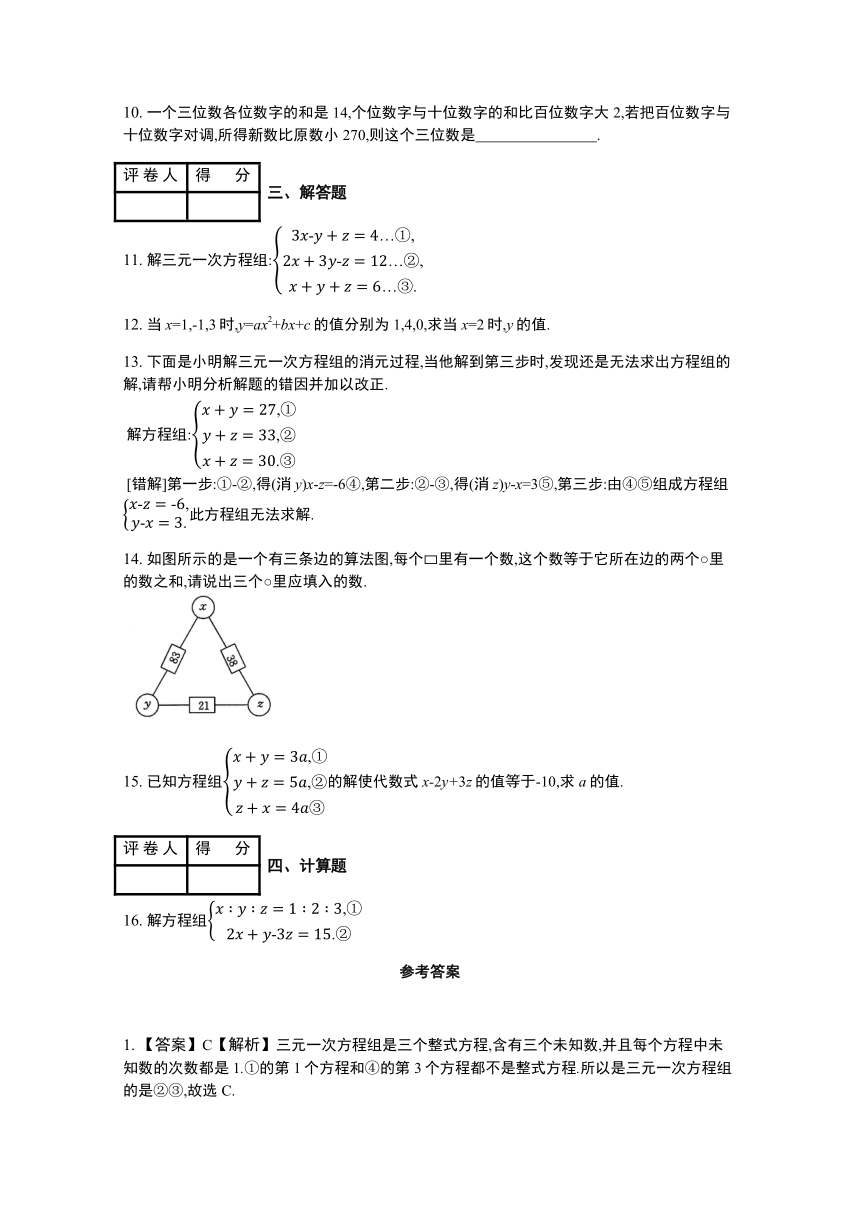
10. 一个三位数各位数字的和是14,个位数字与十位数字的和比百位数字大2,若把百位数字与十位数字对调,所得新数比原数小270,则这个三位数是 .
评卷人 得分 三、解答题
11. 解三元一次方程组:
12. 当x=1,-1,3时,y=ax2+bx+c的值分别为1,4,0,求当x=2时,y的值.
13. 下面是小明解三元一次方程组的消元过程,当他解到第三步时,发现还是无法求出方程组的解,请帮小明分析解题的错因并加以改正.
解方程组:
[错解]第一步:①-②,得(消y)x-z=-6④,第二步:②-③,得(消z)y-x=3⑤,第三步:由④⑤组成方程组此方程组无法求解.
14. 如图所示的是一个有三条边的算法图,每个 里有一个数,这个数等于它所在边的两个○里的数之和,请说出三个○里应填入的数.
15. 已知方程组的解使代数式x-2y+3z的值等于-10,求a的值.
评卷人 得分 四、计算题
16. 解方程组
参考答案
1. 【答案】C【解析】三元一次方程组是三个整式方程,含有三个未知数,并且每个方程中未知数的次数都是1.①的第1个方程和④的第3个方程都不是整式方程.所以是三元一次方程组的是②③,故选C.
2. 【答案】B【解析】∵y的系数的绝对值都是1,∴消去y较简便.故选B.
3. 【答案】C【解析】方程组由①得x=z+4.④由②得y=(z+1).⑤
把④⑤代入③,得(z+4)+(z+1)-z=-1,解得z=-11.把z=-11分别代入④⑤,得x=-7,y=-5.
所以原方程组的解为故选C.
4. 【答案】C【解析】把方程组中的三个方程相加得2(x+y+z)=3+(-2)+9=10,即x+y+z=5,故选C.
5. 【答案】B【解析】设第一小组有x人,第二小组有y人,第三小组有z人,
则由题意得则y=20-3x.
当x=2时,y=14,z=4,符合题意;
当x=3时,y=11,z=6,符合题意;
当x=4时,y=8,z=8,符合题意;
当x=5时,y=5,z=10,符合题意;
当x=6时,y=2,z=12,符合题意.
故学生分组方案有5种.故选B.
6. 【答案】5
【解析】x+2y+3z=10①,4x+3y+2z=15②,①+②得:5x+5y+5z=25,∴x+y+z=5.
7. 【答案】4
【解析】由同类项的定义,可列出方程组解得所以x-y+z=4.
8. 【答案】18
【解析】由题意得解得
所以y=x2+x-2.当x=4时得y=42+4-2=18.
9. 【答案】1;2;3
【解析】∵三个非负数的和为0,∴每个非负数都为0,
由此可得方程组解得
10. 【答案】635
【解析】设这个三位数的个位数字为x,十位数字为y,百位数字为z.
由题意列方程组,得
解得故这个三位数是635.
11. 【答案】①+②得5x+2y=16…④,
③+②得3x+4y=18…⑤,
得方程组
解得,
代入③得2+3+z=6,
∴z=1.
∴方程组的解为
12. 【答案】由题意得:解得
∴y=x2-x+.
当x=2时,y=×22-×2+=1-3+.
13. 【答案】错解原因是消元的目的不明确,消元时,应始终对同一个未知数进行,否则就达不到消元的目的.
正解:②-③,得y-x=3,④,
由①④组成方程组解得
将x=12代入③,得z=18.
∴方程组的解为
14. 【答案】由题意列方程得
①+②+③,得2(x+y+z)=142,即x+y+z=71.④
④-①,得z=-12,④-②,得x=50,④-③,得y=33.
∴三元一次方程组的解为
15. 【答案】解法1:②-①,得z-x=2a.④
③+④,得2z=6a,即z=3a.
把z=3a分别代入②和③,得y=2a,x=a.所以
把x=a,y=2a,z=3a代入x-2y+3z=-10,得
a-2×2a+3×3a=-10,解得a=-.
解法2:①+②+③,得2(x+y+z)=12a,
即x+y+z=6a.④
④-①,得z=3a.④-②,得x=a.
④-③,得y=2a.所以
以下同解法1,略.
16. 【答案】设x=k,y=2k,z=3k,代入②得:2k+2k-9k=15.
解得k=-3.
所以原方程组的解为
学校: 姓名: 班级: 考号:
评卷人 得分 一、选择题
1. 下列各方程组中,是三元一次方程组的是( )
①②
③④
A. ①②④ B. ①②③ C. ②③ D. ①②③④
2. 解方程组若要使运算简便,消元的方法应选( )
A. 消去x B. 消去y C. 消去z D. 以上说法都不对
3. 方程组的解是( )
A. B. C. D.
4. 已知方程组则x+y+z的值为( )
A. 6 B. -6 C. 5 D. -5
5. 某校团委与社区联合举办“保护地球,人人有责”活动,选派20名学生分三组到120个店铺发传单,若第一,二,三小组每人分别负责8,6,5个店铺,且每组至少有两人,则学生分组方案有( )
A. 6种 B. 5种 C. 4种 D. 3种
评卷人 得分 二、填空题
6. 若x+2y+3z=10,4x+3y+2z=15,则x+y+z的值是 .
7. 已知2ay+5b3x+ycz-x与-4a2xb5cy是同类项,则x-y+z的值为 .
8. 在y=ax2+bx+c中,当x=1时,y=0;当x=2时,y=4;当x=3时,y=10,则当x=4时,y= .
9. 若|a+b-3|+(5a-b-c)2+|2c+b-8|=0,则a= ,b= ,c= .
10. 一个三位数各位数字的和是14,个位数字与十位数字的和比百位数字大2,若把百位数字与十位数字对调,所得新数比原数小270,则这个三位数是 .
评卷人 得分 三、解答题
11. 解三元一次方程组:
12. 当x=1,-1,3时,y=ax2+bx+c的值分别为1,4,0,求当x=2时,y的值.
13. 下面是小明解三元一次方程组的消元过程,当他解到第三步时,发现还是无法求出方程组的解,请帮小明分析解题的错因并加以改正.
解方程组:
[错解]第一步:①-②,得(消y)x-z=-6④,第二步:②-③,得(消z)y-x=3⑤,第三步:由④⑤组成方程组此方程组无法求解.
14. 如图所示的是一个有三条边的算法图,每个 里有一个数,这个数等于它所在边的两个○里的数之和,请说出三个○里应填入的数.
15. 已知方程组的解使代数式x-2y+3z的值等于-10,求a的值.
评卷人 得分 四、计算题
16. 解方程组
参考答案
1. 【答案】C【解析】三元一次方程组是三个整式方程,含有三个未知数,并且每个方程中未知数的次数都是1.①的第1个方程和④的第3个方程都不是整式方程.所以是三元一次方程组的是②③,故选C.
2. 【答案】B【解析】∵y的系数的绝对值都是1,∴消去y较简便.故选B.
3. 【答案】C【解析】方程组由①得x=z+4.④由②得y=(z+1).⑤
把④⑤代入③,得(z+4)+(z+1)-z=-1,解得z=-11.把z=-11分别代入④⑤,得x=-7,y=-5.
所以原方程组的解为故选C.
4. 【答案】C【解析】把方程组中的三个方程相加得2(x+y+z)=3+(-2)+9=10,即x+y+z=5,故选C.
5. 【答案】B【解析】设第一小组有x人,第二小组有y人,第三小组有z人,
则由题意得则y=20-3x.
当x=2时,y=14,z=4,符合题意;
当x=3时,y=11,z=6,符合题意;
当x=4时,y=8,z=8,符合题意;
当x=5时,y=5,z=10,符合题意;
当x=6时,y=2,z=12,符合题意.
故学生分组方案有5种.故选B.
6. 【答案】5
【解析】x+2y+3z=10①,4x+3y+2z=15②,①+②得:5x+5y+5z=25,∴x+y+z=5.
7. 【答案】4
【解析】由同类项的定义,可列出方程组解得所以x-y+z=4.
8. 【答案】18
【解析】由题意得解得
所以y=x2+x-2.当x=4时得y=42+4-2=18.
9. 【答案】1;2;3
【解析】∵三个非负数的和为0,∴每个非负数都为0,
由此可得方程组解得
10. 【答案】635
【解析】设这个三位数的个位数字为x,十位数字为y,百位数字为z.
由题意列方程组,得
解得故这个三位数是635.
11. 【答案】①+②得5x+2y=16…④,
③+②得3x+4y=18…⑤,
得方程组
解得,
代入③得2+3+z=6,
∴z=1.
∴方程组的解为
12. 【答案】由题意得:解得
∴y=x2-x+.
当x=2时,y=×22-×2+=1-3+.
13. 【答案】错解原因是消元的目的不明确,消元时,应始终对同一个未知数进行,否则就达不到消元的目的.
正解:②-③,得y-x=3,④,
由①④组成方程组解得
将x=12代入③,得z=18.
∴方程组的解为
14. 【答案】由题意列方程得
①+②+③,得2(x+y+z)=142,即x+y+z=71.④
④-①,得z=-12,④-②,得x=50,④-③,得y=33.
∴三元一次方程组的解为
15. 【答案】解法1:②-①,得z-x=2a.④
③+④,得2z=6a,即z=3a.
把z=3a分别代入②和③,得y=2a,x=a.所以
把x=a,y=2a,z=3a代入x-2y+3z=-10,得
a-2×2a+3×3a=-10,解得a=-.
解法2:①+②+③,得2(x+y+z)=12a,
即x+y+z=6a.④
④-①,得z=3a.④-②,得x=a.
④-③,得y=2a.所以
以下同解法1,略.
16. 【答案】设x=k,y=2k,z=3k,代入②得:2k+2k-9k=15.
解得k=-3.
所以原方程组的解为
