11.2.1.1 三角形内角和定理 课件(共15张PPT)
文档属性
| 名称 | 11.2.1.1 三角形内角和定理 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 901.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 16:42:34 | ||
图片预览





文档简介
(共15张PPT)
人教版 八年级上册
11.2 与三角形有关的角
11.2.1 三角形的内角
11.2.1.1 三角形内角和定理
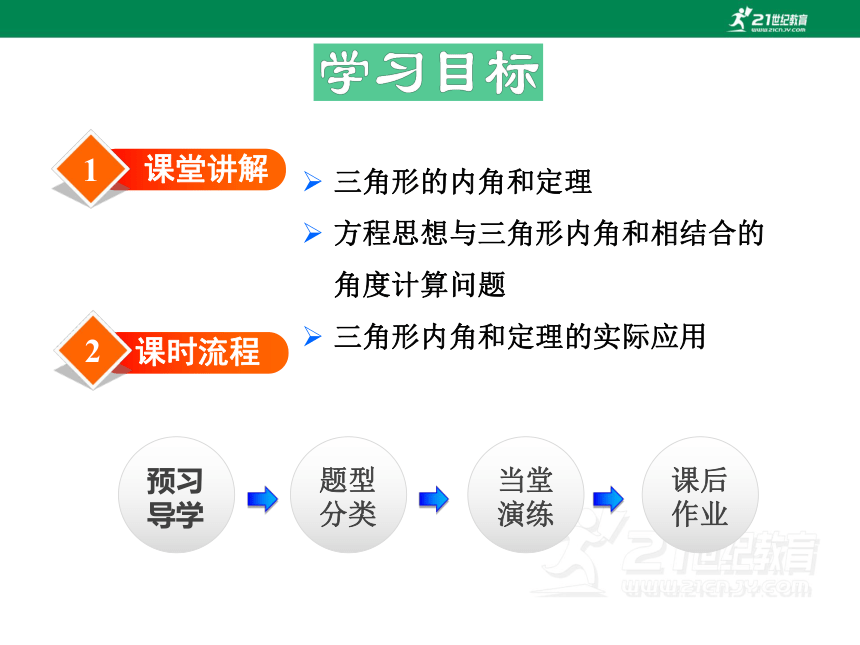
1
课堂讲解
三角形的内角和定理
方程思想与三角形内角和相结合的角度计算问题
三角形内角和定理的实际应用
2
课时流程
当堂演练
预习导学
题型分类
课后作业
三角形内角和定理
定理:三角形三个内角的和等于_______.
180°
【例1】 如图,在△ABC中,∠A=36°,∠C=72°,BD平分∠ABC,求∠DBC的度数.
一
题型
三角形的内角和定理
解:∵∠A=36°,∠C=72°,
∴∠ABC=180°-∠A-∠C= 180°-36°-72°=72°,
∵BD平分∠ABC,
∴∠DBC= ∠ABC= ×72°=36°.
二
题型
方程思想与三角形内角和相结合的角度计算问题
【例2】 在△ABC中,∠A= ∠B= ∠C,求∠A的度数.
解:∵∠A= ∠B= ∠C,
∴∠B=2∠A,∠C=3∠A,
由三角形内角和定理,得∠A+2∠A+3∠A=180°,
解得∠A=30°.
【金点子】运用列方程的方法解答有关角度问题.数学中的求值题,多数用列方程的方法来解决.
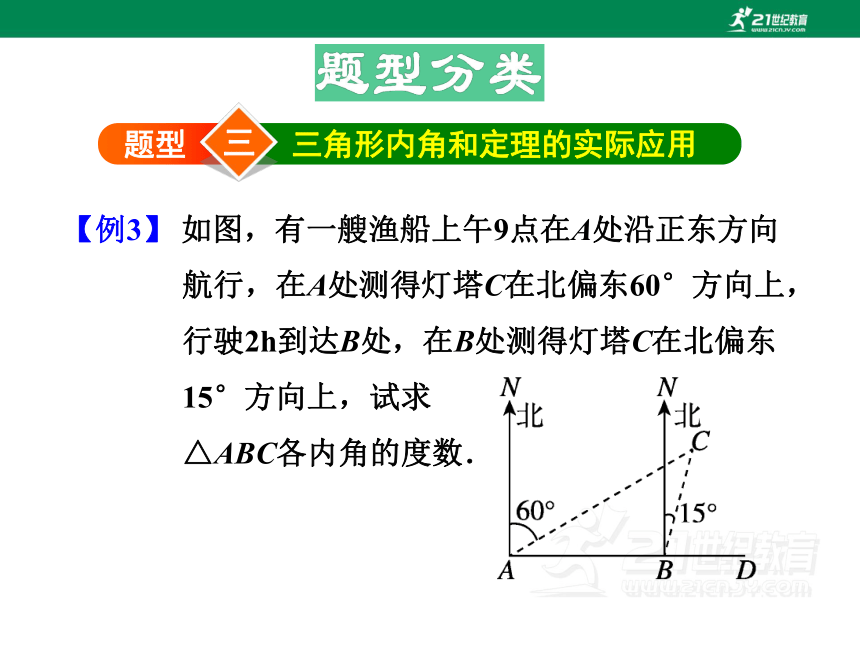
【例3】 如图,有一艘渔船上午9点在A处沿正东方向航行,在A处测得灯塔C在北偏东60°方向上,行驶2h到达B处,在B处测得灯塔C在北偏东15°方向上,试求
△ABC各内角的度数.
三
题型
三角形内角和定理的实际应用
解:∵∠CAB=90°-60°=30°,
∠ABC=90°+15°=105°,
∴∠C=180°-∠CAB-∠CBA=45°.
【金点子】利用三角形内角和与方位角的知识综合求解.
1.(中考 贵港)在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( )
A.35° B.40°
C.45° D.50°
C
2.如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,则从灯塔P观测A,B两处的视角∠P的度数是( )
A.30° B.32°
C.35° D.40°
A
3.如图,∠1+∠2+∠3+∠4=( )
A.360° B.180°
C.280° D.320°
C
4.在△ABC中,已知∠B-∠A=5°,∠C-∠B=20°,求三角形各内角的度数.
解:∵∠B-∠A=5°,∠C-∠B=20°,
∴∠B=5°+∠A,∠C=20°+∠B,
设∠A=x°,则∠B=5°+x°,
∠C=20°+5°+x°=25°+x°,
∵∠A+∠B+∠C=180°,
即x°+5°+x°+25°+x°=180°,解得x=50,
∴∠A=50°,∠B=55°,∠C=75°.
请完成本课时对应的课外演练
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
11.2 与三角形有关的角
11.2.1 三角形的内角
11.2.1.1 三角形内角和定理
1
课堂讲解
三角形的内角和定理
方程思想与三角形内角和相结合的角度计算问题
三角形内角和定理的实际应用
2
课时流程
当堂演练
预习导学
题型分类
课后作业
三角形内角和定理
定理:三角形三个内角的和等于_______.
180°
【例1】 如图,在△ABC中,∠A=36°,∠C=72°,BD平分∠ABC,求∠DBC的度数.
一
题型
三角形的内角和定理
解:∵∠A=36°,∠C=72°,
∴∠ABC=180°-∠A-∠C= 180°-36°-72°=72°,
∵BD平分∠ABC,
∴∠DBC= ∠ABC= ×72°=36°.
二
题型
方程思想与三角形内角和相结合的角度计算问题
【例2】 在△ABC中,∠A= ∠B= ∠C,求∠A的度数.
解:∵∠A= ∠B= ∠C,
∴∠B=2∠A,∠C=3∠A,
由三角形内角和定理,得∠A+2∠A+3∠A=180°,
解得∠A=30°.
【金点子】运用列方程的方法解答有关角度问题.数学中的求值题,多数用列方程的方法来解决.
【例3】 如图,有一艘渔船上午9点在A处沿正东方向航行,在A处测得灯塔C在北偏东60°方向上,行驶2h到达B处,在B处测得灯塔C在北偏东15°方向上,试求
△ABC各内角的度数.
三
题型
三角形内角和定理的实际应用
解:∵∠CAB=90°-60°=30°,
∠ABC=90°+15°=105°,
∴∠C=180°-∠CAB-∠CBA=45°.
【金点子】利用三角形内角和与方位角的知识综合求解.
1.(中考 贵港)在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( )
A.35° B.40°
C.45° D.50°
C
2.如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,则从灯塔P观测A,B两处的视角∠P的度数是( )
A.30° B.32°
C.35° D.40°
A
3.如图,∠1+∠2+∠3+∠4=( )
A.360° B.180°
C.280° D.320°
C
4.在△ABC中,已知∠B-∠A=5°,∠C-∠B=20°,求三角形各内角的度数.
解:∵∠B-∠A=5°,∠C-∠B=20°,
∴∠B=5°+∠A,∠C=20°+∠B,
设∠A=x°,则∠B=5°+x°,
∠C=20°+5°+x°=25°+x°,
∵∠A+∠B+∠C=180°,
即x°+5°+x°+25°+x°=180°,解得x=50,
∴∠A=50°,∠B=55°,∠C=75°.
请完成本课时对应的课外演练
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
