11.1.2 三角形的高、中线与角平分线 课件(共17张PPT)
文档属性
| 名称 | 11.1.2 三角形的高、中线与角平分线 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 929.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 16:25:52 | ||
图片预览





文档简介
(共17张PPT)
人教版 八年级上册
11.1 与三角形有关的线段
11.1.2 三角形的高、中线与角平分线
1
课堂讲解
三角形的高、中线与角平分线的概念
三角形的面积
2
课时流程
当堂演练
预习导学
题型分类
课后作业
1.三角形的高、中线与角平分线的概念
高:从三角形的一个顶点向它所对的边所在的直线画垂线,顶点和垂足之间的线段叫做三角形的高.
中线:在三角形中,连接一个顶点和它所对的边的中点的线段,叫做三角形的中线.
角平分线:在三角形中,一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
注意:三角形的高、中线与角平分线均是_______.
线段
2.三角形的重心及面积公式
重心:三角形_______________叫做三角形的重心.
面积公式:S= ah(a是三角形的边,h是这条边上的高).
规律:三角形一边上的中线将三角形分成面积相等的两部分.
三条中线的交点
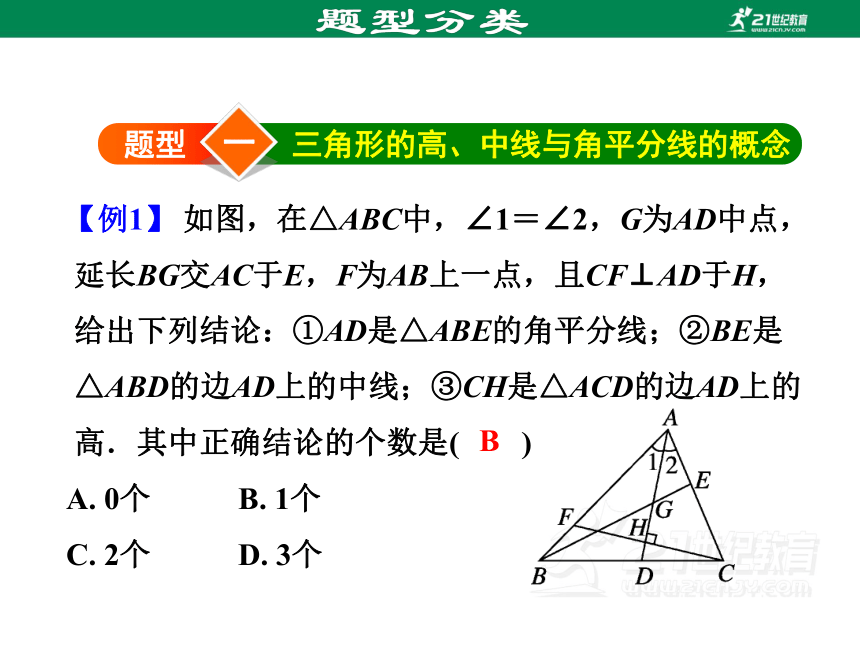
【例1】 如图,在△ABC中,∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,且CF⊥AD于H,给出下列结论:①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH是△ACD的边AD上的高.其中正确结论的个数是( )
A. 0个 B. 1个
C. 2个 D. 3个
一
题型
三角形的高、中线与角平分线的概念
B
【金点子】三角形的角平分线、中线、高是三角形中的三种重要线段,掌握它们的概念是关键.
二
题型
三角形的面积
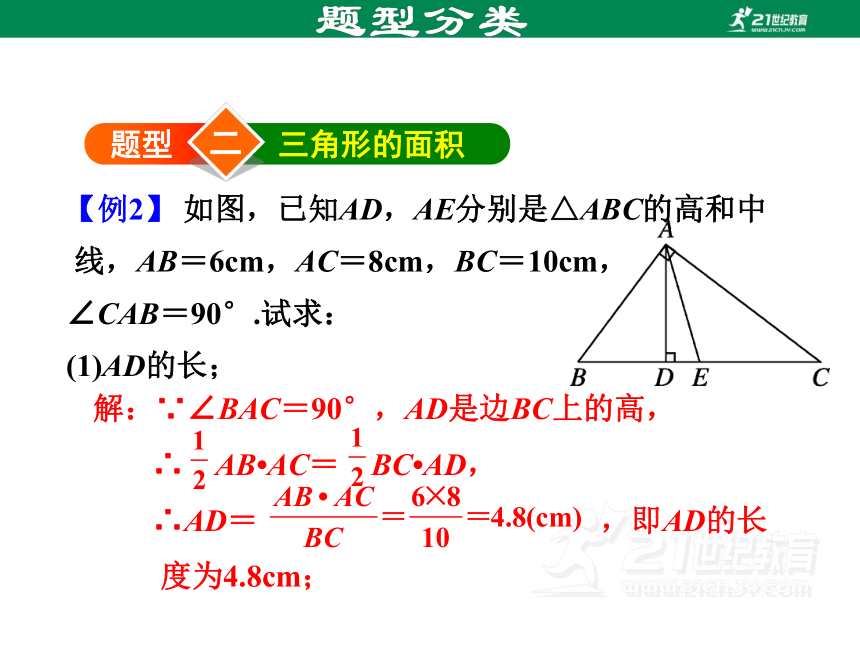
【例2】 如图,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,
∠CAB=90°.试求:
(1)AD的长;
解:∵∠BAC=90°,AD是边BC上的高,
∴ AB AC= BC AD,
∴AD= ,即AD的长度为4.8cm;
解:∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC= AB AC= ×6×8=24(cm2).
又∵AE是边BC上的中线,∴BE=EC,
∴ BE AD= EC AD,即S△ABE=S△AEC,
∴S△ABE= S△ABC=12cm2.
即△ABE的面积是12cm2.
(2)△ABE的面积;
(3)△ACE和△ABE的周长差.
解:∵AE为边BC上的中线, ∴BE=CE,
∴△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=8-6=2(cm),
即△ACE和△ABE的周长差是2cm.
【金点子】(1)利用面积公式可以求直角三角形斜边上的高;(2)三角形一边上的中线把三角形的面积两等分.
1.下面四个图形中,线段BE是△ABC的高的图是 ( )
A
A
B
C
D
2.三角形的下列线段中,能将三角形分成面积相等的两部分的是( )
A.中线 B.角平分线
C.高 D.边
A
3.如图,已知∠1=∠2,∠3=∠4,则下列结论正确的个数为( )
①AD平分∠BAF;
②AF平分∠DAC;
③AE平分∠DAF;
④AE平分∠BAC.
A.1 B.2 C.3 D.4
B
4.如图,在△ABC中,AD⊥BC,BE⊥AC,BC=12,AC=8,AD=6,BE的长为多少?
解:∵在△ABC中,AD⊥BC,BE⊥AC,
∴S△ABC= BC AD,S△ABC= AC BE.
∴BC AD=AC BE,
∵BC=12,AC=8,AD=6,
请完成本课时对应的课外演练
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
11.1 与三角形有关的线段
11.1.2 三角形的高、中线与角平分线
1
课堂讲解
三角形的高、中线与角平分线的概念
三角形的面积
2
课时流程
当堂演练
预习导学
题型分类
课后作业
1.三角形的高、中线与角平分线的概念
高:从三角形的一个顶点向它所对的边所在的直线画垂线,顶点和垂足之间的线段叫做三角形的高.
中线:在三角形中,连接一个顶点和它所对的边的中点的线段,叫做三角形的中线.
角平分线:在三角形中,一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
注意:三角形的高、中线与角平分线均是_______.
线段
2.三角形的重心及面积公式
重心:三角形_______________叫做三角形的重心.
面积公式:S= ah(a是三角形的边,h是这条边上的高).
规律:三角形一边上的中线将三角形分成面积相等的两部分.
三条中线的交点
【例1】 如图,在△ABC中,∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,且CF⊥AD于H,给出下列结论:①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH是△ACD的边AD上的高.其中正确结论的个数是( )
A. 0个 B. 1个
C. 2个 D. 3个
一
题型
三角形的高、中线与角平分线的概念
B
【金点子】三角形的角平分线、中线、高是三角形中的三种重要线段,掌握它们的概念是关键.
二
题型
三角形的面积
【例2】 如图,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,
∠CAB=90°.试求:
(1)AD的长;
解:∵∠BAC=90°,AD是边BC上的高,
∴ AB AC= BC AD,
∴AD= ,即AD的长度为4.8cm;
解:∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC= AB AC= ×6×8=24(cm2).
又∵AE是边BC上的中线,∴BE=EC,
∴ BE AD= EC AD,即S△ABE=S△AEC,
∴S△ABE= S△ABC=12cm2.
即△ABE的面积是12cm2.
(2)△ABE的面积;
(3)△ACE和△ABE的周长差.
解:∵AE为边BC上的中线, ∴BE=CE,
∴△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=8-6=2(cm),
即△ACE和△ABE的周长差是2cm.
【金点子】(1)利用面积公式可以求直角三角形斜边上的高;(2)三角形一边上的中线把三角形的面积两等分.
1.下面四个图形中,线段BE是△ABC的高的图是 ( )
A
A
B
C
D
2.三角形的下列线段中,能将三角形分成面积相等的两部分的是( )
A.中线 B.角平分线
C.高 D.边
A
3.如图,已知∠1=∠2,∠3=∠4,则下列结论正确的个数为( )
①AD平分∠BAF;
②AF平分∠DAC;
③AE平分∠DAF;
④AE平分∠BAC.
A.1 B.2 C.3 D.4
B
4.如图,在△ABC中,AD⊥BC,BE⊥AC,BC=12,AC=8,AD=6,BE的长为多少?
解:∵在△ABC中,AD⊥BC,BE⊥AC,
∴S△ABC= BC AD,S△ABC= AC BE.
∴BC AD=AC BE,
∵BC=12,AC=8,AD=6,
请完成本课时对应的课外演练
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
