11.2.1.2 直角三角形的性质与判定 习题课件(共13张PPT)
文档属性
| 名称 | 11.2.1.2 直角三角形的性质与判定 习题课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 883.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 15:54:33 | ||
图片预览




文档简介
(共13张PPT)
人教版 八年级上册
11.2 与三角形有关的角
11.2.1 三角形的内角
第2课时 直角三角形的性质与判定
1
2
3
4
5
6
7
8
9
1.在一个直角三角形中,两个锐角相等,则这两个锐角的度数是____.
2.如图,AB,CD相交于点O,AC⊥CD于点C,若∠BOD=38°,则∠A等于____.
返回
45°
52°
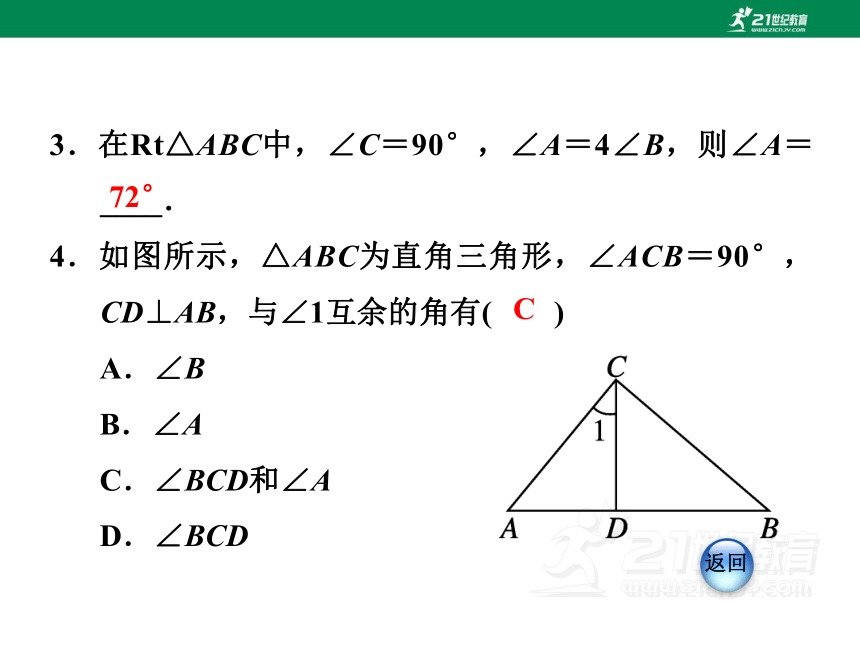
3.在Rt△ABC中,∠C=90°,∠A=4∠B,则∠A=____.
4.如图所示,△ABC为直角三角形,∠ACB=90°,CD⊥AB,与∠1互余的角有( )
A.∠B
B.∠A
C.∠BCD和∠A
D.∠BCD
72°
C
返回
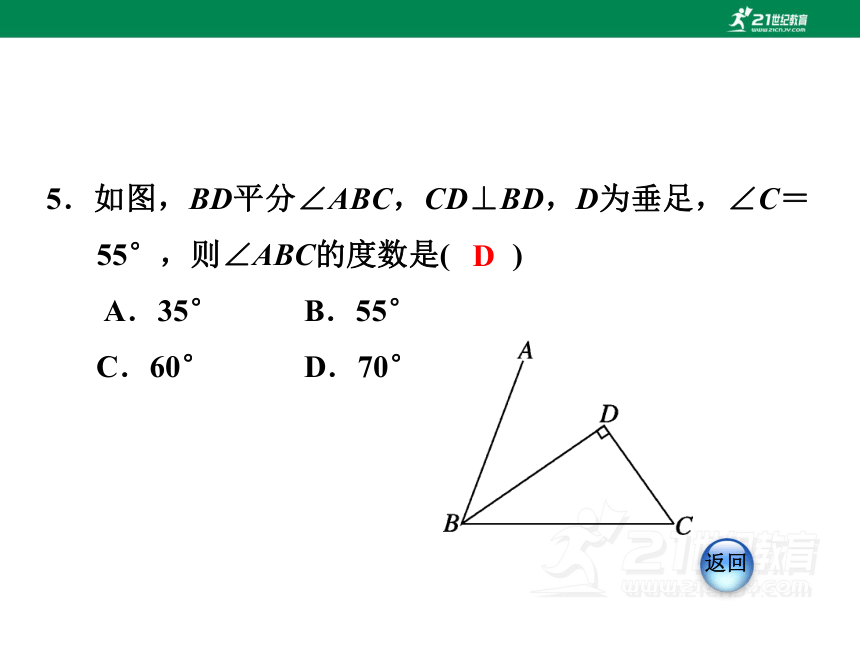
5.如图,BD平分∠ABC,CD⊥BD,D为垂足,∠C=55°,则∠ABC的度数是( )
A.35° B.55°
C.60° D.70°
D
返回
6.如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
求证:△ACD是直角三角形.
证明:∵∠ACB=90°,∴∠A+∠B=90°,
∵∠ACD=∠B,∴∠A+∠ACD=90°,
∴∠ADC=90°,
∴△ACD是直角三角形.
返回
7.如图,Rt△ABC中,∠C=90°,∠CAB、∠CBA的平分线AD、BE交于F,求∠AFB的度数.
解:∵∠C=90°,
∴∠CAB+∠CBA=90°,
∵AD、BE平分∠CAB、∠CBA,
∴∠FAB+∠FBA=45°,
∴∠AFB=135°.
返回
8.如图,AB∥CD,直线EF分别交AB,CD于点E, F,∠BEF的平分线与∠DFE的平分线相交于点P,试说明△EPF为直角三角形.
解:
返回
∵AB∥CD,
∴∠BEF+∠DFE=180°.
∵EP为∠BEF的平分线,FP为∠EFD的平分线,
∴∠PEF= ∠BEF,∠PFE= ∠DFE.
∴∠PEF+∠PFE= (∠BEF+∠DFE)= ×180°=90°.
∴∠EPF=180°-(∠PEF+∠PFE)=90°.
∴△EPF为直角三角形.
9.如图,在△ACB中,∠ACB=90°,CD⊥AB于D.
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
证明:(1)∵∠ACB=90°,
CD⊥AB于D,
∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,
∴∠ACD=∠B;
(2)在Rt△AFC中,∠CFA=90°-∠CAF,
同理在Rt△AED中,∠AED=90°-∠DAE.
又∵AF平分∠CAB,
∴∠CAF=∠DAE,
∴∠AED=∠CFE,
又∵∠CEF=∠AED,
∴∠CEF=∠CFE.
证明:
返回
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
11.2 与三角形有关的角
11.2.1 三角形的内角
第2课时 直角三角形的性质与判定
1
2
3
4
5
6
7
8
9
1.在一个直角三角形中,两个锐角相等,则这两个锐角的度数是____.
2.如图,AB,CD相交于点O,AC⊥CD于点C,若∠BOD=38°,则∠A等于____.
返回
45°
52°
3.在Rt△ABC中,∠C=90°,∠A=4∠B,则∠A=____.
4.如图所示,△ABC为直角三角形,∠ACB=90°,CD⊥AB,与∠1互余的角有( )
A.∠B
B.∠A
C.∠BCD和∠A
D.∠BCD
72°
C
返回
5.如图,BD平分∠ABC,CD⊥BD,D为垂足,∠C=55°,则∠ABC的度数是( )
A.35° B.55°
C.60° D.70°
D
返回
6.如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
求证:△ACD是直角三角形.
证明:∵∠ACB=90°,∴∠A+∠B=90°,
∵∠ACD=∠B,∴∠A+∠ACD=90°,
∴∠ADC=90°,
∴△ACD是直角三角形.
返回
7.如图,Rt△ABC中,∠C=90°,∠CAB、∠CBA的平分线AD、BE交于F,求∠AFB的度数.
解:∵∠C=90°,
∴∠CAB+∠CBA=90°,
∵AD、BE平分∠CAB、∠CBA,
∴∠FAB+∠FBA=45°,
∴∠AFB=135°.
返回
8.如图,AB∥CD,直线EF分别交AB,CD于点E, F,∠BEF的平分线与∠DFE的平分线相交于点P,试说明△EPF为直角三角形.
解:
返回
∵AB∥CD,
∴∠BEF+∠DFE=180°.
∵EP为∠BEF的平分线,FP为∠EFD的平分线,
∴∠PEF= ∠BEF,∠PFE= ∠DFE.
∴∠PEF+∠PFE= (∠BEF+∠DFE)= ×180°=90°.
∴∠EPF=180°-(∠PEF+∠PFE)=90°.
∴△EPF为直角三角形.
9.如图,在△ACB中,∠ACB=90°,CD⊥AB于D.
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
证明:(1)∵∠ACB=90°,
CD⊥AB于D,
∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,
∴∠ACD=∠B;
(2)在Rt△AFC中,∠CFA=90°-∠CAF,
同理在Rt△AED中,∠AED=90°-∠DAE.
又∵AF平分∠CAB,
∴∠CAF=∠DAE,
∴∠AED=∠CFE,
又∵∠CEF=∠AED,
∴∠CEF=∠CFE.
证明:
返回
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
