11.2.1.1 三角形内角和定理 习题课件(共14张PPT)
文档属性
| 名称 | 11.2.1.1 三角形内角和定理 习题课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 885.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 15:51:13 | ||
图片预览






文档简介
(共14张PPT)
人教版 八年级上册
11.2 与三角形有关的角
11.2.1 三角形的内角
11.2.1.1 三角形内角和定理
1
2
3
4
5
6
7
8
9
10
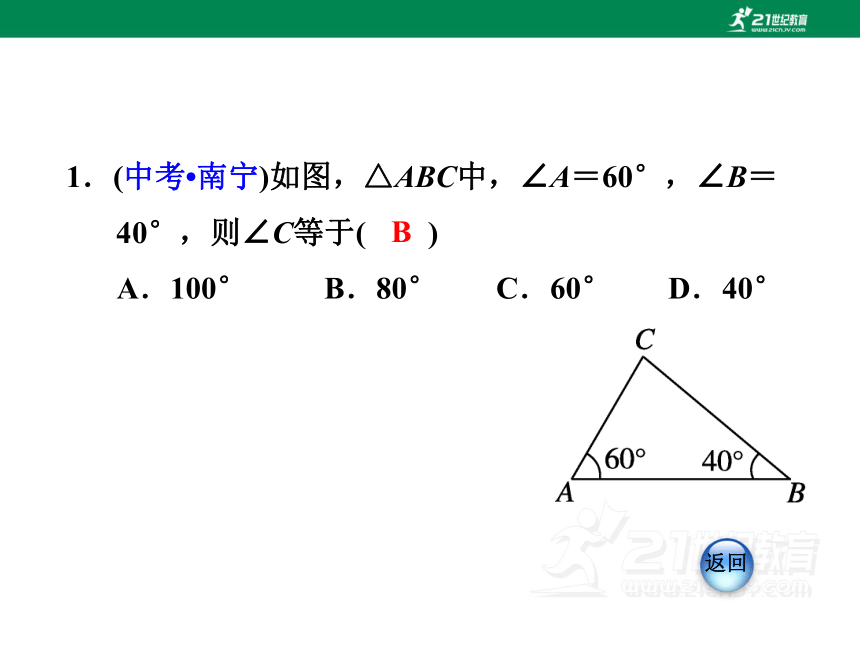
1.(中考 南宁)如图,△ABC中,∠A=60°,∠B=40°,则∠C等于( )
A.100° B.80° C.60° D.40°
返回
B
2.在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )
A.等边三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
返回
D
返回
3.在△ABC中,∠A ∶∠B ∶∠C=3 ∶4 ∶5,则∠C等于( )
A.45° B.60°
C.75° D.90°
C
4.如图,点O是△ABC内一点,∠A=80°,BO、CO分别是∠ABC和∠ACB的平分线,则∠BOC等于( )
A.140° B.120°
C.130° D.无法确定
返回
C
5.如图,△ABC中,点D、E分别在AB、AC边上,DE∥BC,∠A=50°,∠C=70°,那么∠ADE的度数是_______.
返回
60°
6.如图,△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠ADE=155°,则∠B的度数为______.
返回
65°
7.如图,将∠BAC沿DE向∠BAC内折叠,使AD与A′D重合,AE与A′E重合,若∠A=30°,则∠1+ ∠2=_______.
返回
60°
8.如图,在△ABC中,∠A=46°,CE是∠ACB的平分线,B,C,D在同一条直线上,DF∥EC,∠D=42°.求∠B的度数.
返回
解:∵FD∥EC,∠D=42°,
∴∠BCE=∠D=42°,
∵CE是∠ACB的平分线,
∴∠ACB=2∠BCE=84°,
∵∠A=46°,
∴∠B=180°-84°-46°=50°.
9.如图,已知D为△ABC的边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.
解:∵∠AFE=90°,
∴∠AEF=90°-∠A=90°-35°
=55°,
∴∠CED=∠AEF=55°,
∴∠ACD=180°-∠CED-∠D=180°-55°-42°=83°.
10.如图,△ABC中,∠ACB=∠ABC,∠A=40°,P是△ABC内一点,且∠1=∠2,求∠BPC的度数.
解:∵∠A=40°,∠ACB=∠ABC,
∴∠ACB=∠ABC=70°.
又∵∠1=∠2,
∴∠BCP=∠ABP.
∴∠2+∠BCP=70°.
∴∠BPC=180°-(∠2+∠BCP)=110°.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
11.2 与三角形有关的角
11.2.1 三角形的内角
11.2.1.1 三角形内角和定理
1
2
3
4
5
6
7
8
9
10
1.(中考 南宁)如图,△ABC中,∠A=60°,∠B=40°,则∠C等于( )
A.100° B.80° C.60° D.40°
返回
B
2.在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )
A.等边三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
返回
D
返回
3.在△ABC中,∠A ∶∠B ∶∠C=3 ∶4 ∶5,则∠C等于( )
A.45° B.60°
C.75° D.90°
C
4.如图,点O是△ABC内一点,∠A=80°,BO、CO分别是∠ABC和∠ACB的平分线,则∠BOC等于( )
A.140° B.120°
C.130° D.无法确定
返回
C
5.如图,△ABC中,点D、E分别在AB、AC边上,DE∥BC,∠A=50°,∠C=70°,那么∠ADE的度数是_______.
返回
60°
6.如图,△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠ADE=155°,则∠B的度数为______.
返回
65°
7.如图,将∠BAC沿DE向∠BAC内折叠,使AD与A′D重合,AE与A′E重合,若∠A=30°,则∠1+ ∠2=_______.
返回
60°
8.如图,在△ABC中,∠A=46°,CE是∠ACB的平分线,B,C,D在同一条直线上,DF∥EC,∠D=42°.求∠B的度数.
返回
解:∵FD∥EC,∠D=42°,
∴∠BCE=∠D=42°,
∵CE是∠ACB的平分线,
∴∠ACB=2∠BCE=84°,
∵∠A=46°,
∴∠B=180°-84°-46°=50°.
9.如图,已知D为△ABC的边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.
解:∵∠AFE=90°,
∴∠AEF=90°-∠A=90°-35°
=55°,
∴∠CED=∠AEF=55°,
∴∠ACD=180°-∠CED-∠D=180°-55°-42°=83°.
10.如图,△ABC中,∠ACB=∠ABC,∠A=40°,P是△ABC内一点,且∠1=∠2,求∠BPC的度数.
解:∵∠A=40°,∠ACB=∠ABC,
∴∠ACB=∠ABC=70°.
又∵∠1=∠2,
∴∠BCP=∠ABP.
∴∠2+∠BCP=70°.
∴∠BPC=180°-(∠2+∠BCP)=110°.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
