第十一章《三角形》本章复习课件(共17张PPT)
文档属性
| 名称 | 第十一章《三角形》本章复习课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 955.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 16:49:31 | ||
图片预览





文档简介
(共17张PPT)
人教版 八年级上册
第十一章 三角形
本章复习课
1
2
3
4
5
6
7
8
9
10
11
12
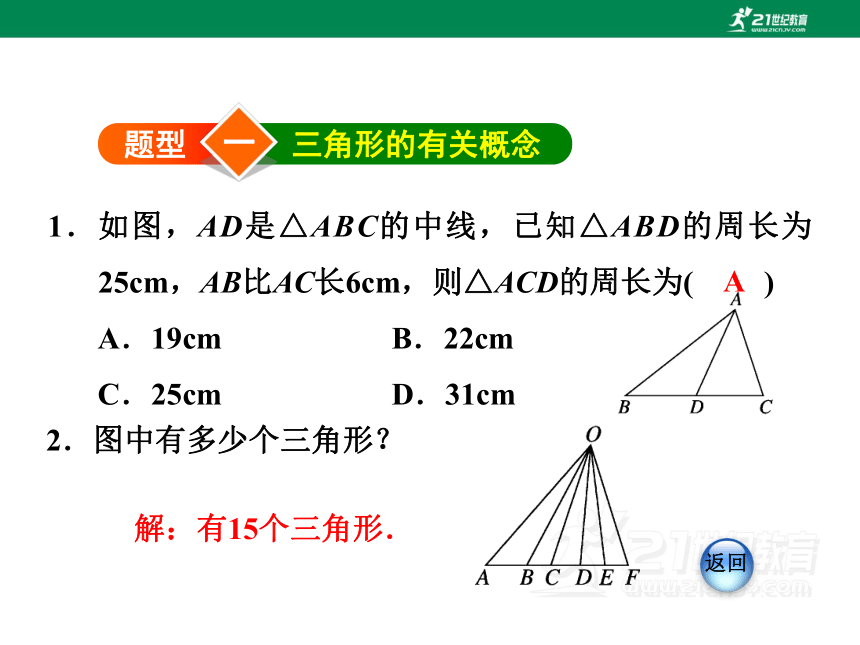
1.如图,AD是△ABC的中线,已知△ABD的周长为25cm,AB比AC长6cm,则△ACD的周长为( )
A.19cm B.22cm
C.25cm D.31cm
返回
A
一
题型
三角形的有关概念
2.图中有多少个三角形?
解:有15个三角形.
3.下列长度的小木棒,把它们首尾顺次相接能摆成一个三角形的是( )
A.1,1,3
B.5,6,7
C.1,8,18
D.3,4,10
返回
B
二
题型
三角形的三边关系
4.若a、b、c为三角形的三边,且a、b满足
+(b-2)2=0,求第三边c的取值范围.
解:由题意知a2-9=0,(b-2)2=0,则a=±3,b=2.因为a>0,所以a=3.由三角形的三边关系,得a-b<c<a+b,即1<c<5.
返回
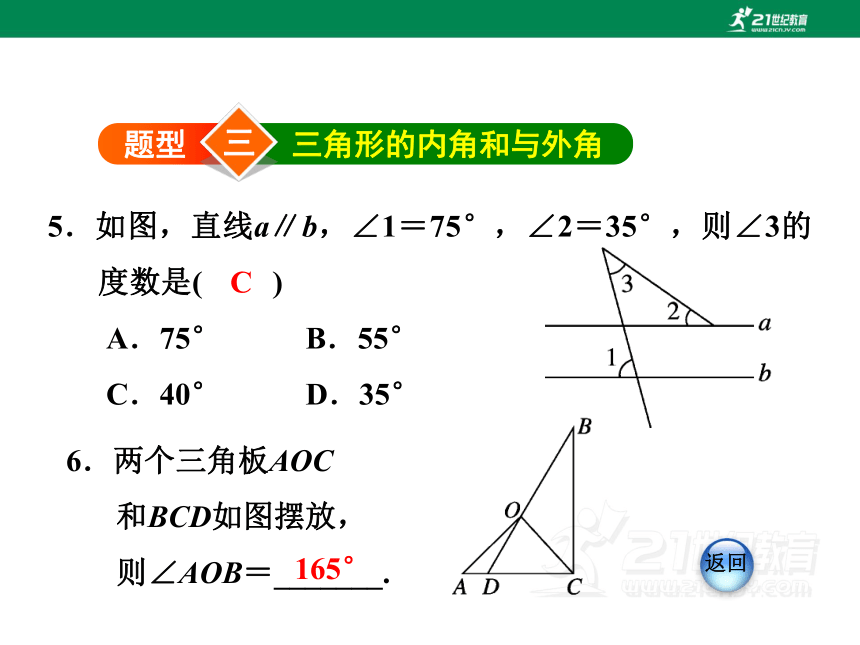
5.如图,直线a∥b,∠1=75°,∠2=35°,则∠3的度数是( )
A.75° B.55°
C.40° D.35°
C
三
题型
三角形的内角和与外角
6.两个三角板AOC
和BCD如图摆放,
则∠AOB=_______.
165°
返回
7.如图,已知∠A=20°,∠B=27°,AC⊥DE,垂足为P,求∠1,∠D的度数.
解:∵AC⊥DE,∴∠APE=90°.
∵∠1是△AEP的外角,
∴∠1=∠A+∠APE.
∵∠A=20°,∴∠1=20°+90°=110°.
在△BDE中,∠1+∠D+∠B=180°,∵∠B=27°,∴∠D=180°-110°-27°=43°.
返回
8.如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E,求∠AEC的度数.
解:
∵∠B=40°,
∴∠BAC+∠BCA=180°-40°=140°,
∴∠DAC+∠FCA=180°-∠BAC+180°-
∠BCA=360°-140°=220°,
∵AE和CE分别平分∠DAC和∠FCA,
∴∠EAC= ∠DAC,∠ECA= ∠FCA,
∴∠EAC+∠ECA= (∠DAC+∠FCA)=110°,
∴∠AEC=180°-(∠EAC+∠ECA)=
180°-110°=70°.
返回
9.如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.
(1)求∠CAD的度数;
解:(1)∵BE平分∠ABC,
∴∠ABC=2∠EBC=64°,
∴∠EBC=32°,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵∠C=∠AEB-∠EBC=70°-32°=38°,
∴∠CAD=90°-38°=52°;
(2)若点F为线段BC上的任意一点,当△EFC为直角三角形时,求∠BEF的度数.
(2)分两种情况:
①当∠EFC=90°时,如答图①所示,则∠BFE=90°,
∴∠BEF=90°-∠EBC=90°-32°=58°;
②当∠FEC=90°时,如答图②所示,
则∠EFC=90°-38°=52°,
∴∠BEF=∠EFC-∠EBC=52°-32°=20°.
综上所述:∠BEF的度数为58°或20°.
返回
10.下列判断中正确的是( )
A.四边形的外角和大于内角和
B.若多边形边数从3增加到n(n为大于3的自然数),它们外角和的度数不变
C.一个多边形的内角中,锐角的个数可以任意多
D.一个多边形的内角和为1 880°
B
四
题型
多边形的内角和与外角和
返回
11.如图,求∠A+∠B+∠C+∠D+∠E+∠F的和.
解:连接AF.
∵在△AOF和△COD中,
∠AOF=∠COD,
∴∠C+∠D=∠OAF+∠OFA,
∴∠DAB+∠B+∠C+∠D+∠E+∠CFE=
∠OAF+∠OFA+∠CFE+∠OAB+∠E+∠B=
∠BAF+∠AFE+∠E+∠B=360°.
返回
12.如图,六边形ABCDEF各内角相等,∠1=∠2=60°,AB与DE有怎样的位置关系?AD与BC有怎样的位置关系?为什么?
AB∥DE,AD∥BC,
∵六边形ABCDEF的内角都相等,
∴六边形ABCDEF的每一个内角都等于120°,
∴∠EDC=∠FAB=120°,
∵∠1=∠2=60°,∴∠EDA=∠DAB=60°,
∴AB∥DE,
∵∠C=120°,∠2=60°,∴∠2+∠C=180°,
∴AD∥BC.
解:
返回
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
第十一章 三角形
本章复习课
1
2
3
4
5
6
7
8
9
10
11
12
1.如图,AD是△ABC的中线,已知△ABD的周长为25cm,AB比AC长6cm,则△ACD的周长为( )
A.19cm B.22cm
C.25cm D.31cm
返回
A
一
题型
三角形的有关概念
2.图中有多少个三角形?
解:有15个三角形.
3.下列长度的小木棒,把它们首尾顺次相接能摆成一个三角形的是( )
A.1,1,3
B.5,6,7
C.1,8,18
D.3,4,10
返回
B
二
题型
三角形的三边关系
4.若a、b、c为三角形的三边,且a、b满足
+(b-2)2=0,求第三边c的取值范围.
解:由题意知a2-9=0,(b-2)2=0,则a=±3,b=2.因为a>0,所以a=3.由三角形的三边关系,得a-b<c<a+b,即1<c<5.
返回
5.如图,直线a∥b,∠1=75°,∠2=35°,则∠3的度数是( )
A.75° B.55°
C.40° D.35°
C
三
题型
三角形的内角和与外角
6.两个三角板AOC
和BCD如图摆放,
则∠AOB=_______.
165°
返回
7.如图,已知∠A=20°,∠B=27°,AC⊥DE,垂足为P,求∠1,∠D的度数.
解:∵AC⊥DE,∴∠APE=90°.
∵∠1是△AEP的外角,
∴∠1=∠A+∠APE.
∵∠A=20°,∴∠1=20°+90°=110°.
在△BDE中,∠1+∠D+∠B=180°,∵∠B=27°,∴∠D=180°-110°-27°=43°.
返回
8.如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E,求∠AEC的度数.
解:
∵∠B=40°,
∴∠BAC+∠BCA=180°-40°=140°,
∴∠DAC+∠FCA=180°-∠BAC+180°-
∠BCA=360°-140°=220°,
∵AE和CE分别平分∠DAC和∠FCA,
∴∠EAC= ∠DAC,∠ECA= ∠FCA,
∴∠EAC+∠ECA= (∠DAC+∠FCA)=110°,
∴∠AEC=180°-(∠EAC+∠ECA)=
180°-110°=70°.
返回
9.如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.
(1)求∠CAD的度数;
解:(1)∵BE平分∠ABC,
∴∠ABC=2∠EBC=64°,
∴∠EBC=32°,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵∠C=∠AEB-∠EBC=70°-32°=38°,
∴∠CAD=90°-38°=52°;
(2)若点F为线段BC上的任意一点,当△EFC为直角三角形时,求∠BEF的度数.
(2)分两种情况:
①当∠EFC=90°时,如答图①所示,则∠BFE=90°,
∴∠BEF=90°-∠EBC=90°-32°=58°;
②当∠FEC=90°时,如答图②所示,
则∠EFC=90°-38°=52°,
∴∠BEF=∠EFC-∠EBC=52°-32°=20°.
综上所述:∠BEF的度数为58°或20°.
返回
10.下列判断中正确的是( )
A.四边形的外角和大于内角和
B.若多边形边数从3增加到n(n为大于3的自然数),它们外角和的度数不变
C.一个多边形的内角中,锐角的个数可以任意多
D.一个多边形的内角和为1 880°
B
四
题型
多边形的内角和与外角和
返回
11.如图,求∠A+∠B+∠C+∠D+∠E+∠F的和.
解:连接AF.
∵在△AOF和△COD中,
∠AOF=∠COD,
∴∠C+∠D=∠OAF+∠OFA,
∴∠DAB+∠B+∠C+∠D+∠E+∠CFE=
∠OAF+∠OFA+∠CFE+∠OAB+∠E+∠B=
∠BAF+∠AFE+∠E+∠B=360°.
返回
12.如图,六边形ABCDEF各内角相等,∠1=∠2=60°,AB与DE有怎样的位置关系?AD与BC有怎样的位置关系?为什么?
AB∥DE,AD∥BC,
∵六边形ABCDEF的内角都相等,
∴六边形ABCDEF的每一个内角都等于120°,
∴∠EDC=∠FAB=120°,
∵∠1=∠2=60°,∴∠EDA=∠DAB=60°,
∴AB∥DE,
∵∠C=120°,∠2=60°,∴∠2+∠C=180°,
∴AD∥BC.
解:
返回
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
