沪科版数学八年级下册 17.1 一元二次方程 课件(共15张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 17.1 一元二次方程 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 146.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
17.1 一元二次方程
导入新课
复习引入
没有未知数
1.下列式子哪些是方程?
2+6=8
2x+3
5x+6=22
x+3y=8
x-5<18
代数式
一元一次方程
二元一次方程
不等式
分式方程
想一想:什么叫一元二次方程呢?
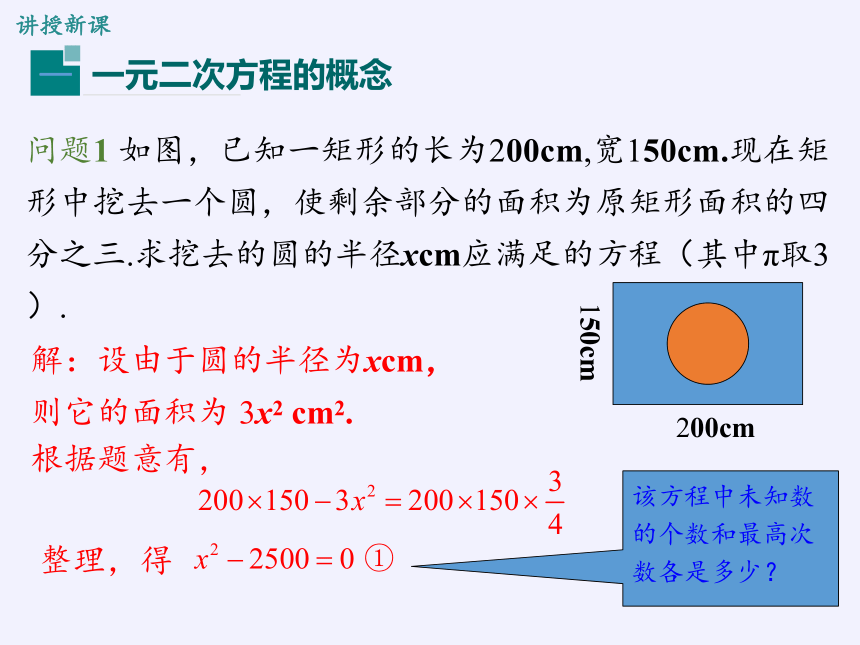
问题1 如图,已知一矩形的长为200cm,宽150cm.现在矩形中挖去一个圆,使剩余部分的面积为原矩形面积的四分之三.求挖去的圆的半径xcm应满足的方程(其中π取3).
解:设由于圆的半径为xcm,则它的面积为 3x2 cm2.
整理,得
该方程中未知数的个数和最高次数各是多少?
一元二次方程的概念
一
讲授新课
根据题意有,
200cm
150cm
问题2 在一块宽20m、长32m的矩形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),把矩形空地分成大小一样的六块,建成小花坛.如图要使花坛的总面积为570m2,问小路的宽应为多少?
32
20
x
1.若设小路的宽是xm,则横向小路的面积______m2,纵向小路的面积是 m2,两者重叠的面积是 m2.
32x
2.由于花坛的总面积是570m2.你能根据题意,列出方程吗?
整理以上方程可得:
思考:
2×20x
32×20-(32x+2×20x)+2x2=570
2x2
x2-36x+35=0 ②
32
20
x
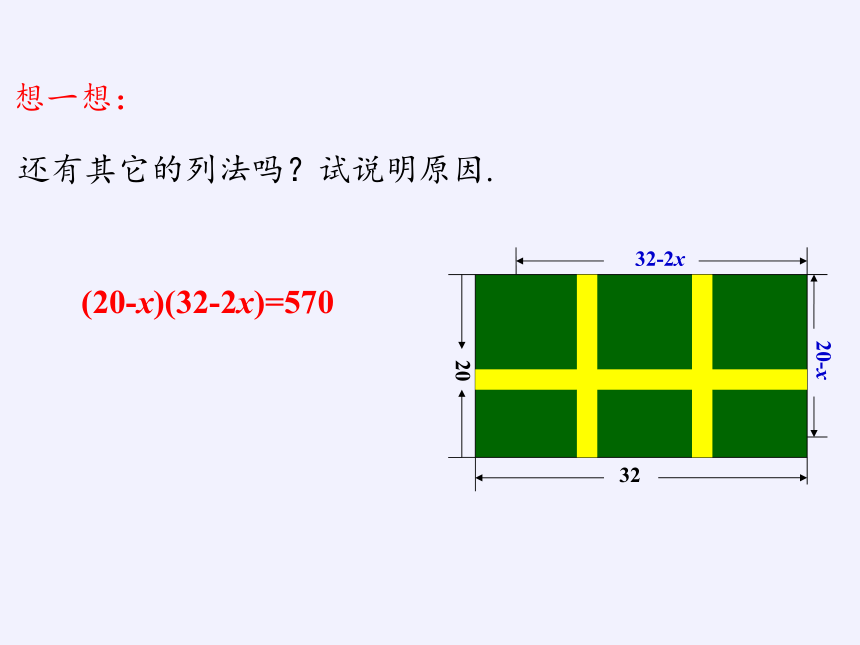
想一想:
还有其它的列法吗?试说明原因.
(20-x)(32-2x)=570
32-2x
20-x
32
20
观察与思考
方程①、②都不是一元一次方程.那么这两个方程与一元一次方程的区别在哪里?它们有什么共同特点呢?
特点:
①都是整式方程;
②只含一个未知数;
③未知数的最高次数是2.
x2-36x+35=0 ②
只含有一个未知数x,并且未知数的最高次数是2的整式方程,叫做一元二次方程.
任何一个关于x的一元二次方程,经过整理都可以化为 ax2+bx +c = 0(a , b , c为常数, a≠0)
ax2 称为二次项, a 称为二次项系数.
bx 称为一次项, b 称为一次项系数.
c 称为常数项.
思考:为什么要限制a≠0,b,c可以为零吗
知识要点
一元二次方程的概念
一元二次方程的一般形式是
典例精析
例1 下列选项中,关于x的一元二次方程的是( )
C
不是整式方程
含两个未知数
化简整理成
x2-3x+2=0
少了限制条件
a≠0
提示
判断一个方程是不是一元二次方程,首先看是不是整式方程;如是再进一步化简整理后再作判断.
例2:将方程3x(x-1)=5(x+2)化为一般形式,并分别指出它们的二次项、一次项和常数项及它们的系数.
解:
去括号,得
3x2-3x=5x+10.
移项、合并同类项,得一元二次方程的一般形式
3x2-8x-10=0.
其中二次项是3x2,系数是3;一次项是-8x,系数是-8;常数项是-10.
系数和项均包含前面的符号.
注意
一元二次方程的根
二
一元二次方程的根
使一元二次方程等号两边相等的未知数的值叫作一元二次方程的解(又叫做根).
例3:下面哪些数是方程 x2 – x – 6 = 0 的解
-4 ,-3 , -2 ,-1 ,0 ,1,2,3 ,4
解:
3和-2.
你注意到了吗?一元二次方程可能不止一个根.
当堂练习
1. 下列哪些是一元二次方程?如果是一元二次方程,化为一般式:
√
×
√
×
×
√
3x+2=5x-2
x2=0
(x+3)(2x-4)=x2
3y2=(3y+1)(y-2)
x2=x3+x2-1
3x2=5x-1
(1)
(4)
(2)
(3)
(6)
(5)
2.填空:
方程 一般形式 二次项系数 一次项系数 常数项
-2
1
3
1
3
-5
4
0
-5
3
-2
课堂小结
一元二次方程
概念
是整式方程;
含一个未知数;
最高次数是2.
一般形式
ax2+bx+c=0 (a ≠0)
其中(a≠0)是一元二次方程的必要条件;
根
使方程左右两边相等的未知数的值.
谢 谢
17.1 一元二次方程
导入新课
复习引入
没有未知数
1.下列式子哪些是方程?
2+6=8
2x+3
5x+6=22
x+3y=8
x-5<18
代数式
一元一次方程
二元一次方程
不等式
分式方程
想一想:什么叫一元二次方程呢?
问题1 如图,已知一矩形的长为200cm,宽150cm.现在矩形中挖去一个圆,使剩余部分的面积为原矩形面积的四分之三.求挖去的圆的半径xcm应满足的方程(其中π取3).
解:设由于圆的半径为xcm,则它的面积为 3x2 cm2.
整理,得
该方程中未知数的个数和最高次数各是多少?
一元二次方程的概念
一
讲授新课
根据题意有,
200cm
150cm
问题2 在一块宽20m、长32m的矩形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),把矩形空地分成大小一样的六块,建成小花坛.如图要使花坛的总面积为570m2,问小路的宽应为多少?
32
20
x
1.若设小路的宽是xm,则横向小路的面积______m2,纵向小路的面积是 m2,两者重叠的面积是 m2.
32x
2.由于花坛的总面积是570m2.你能根据题意,列出方程吗?
整理以上方程可得:
思考:
2×20x
32×20-(32x+2×20x)+2x2=570
2x2
x2-36x+35=0 ②
32
20
x
想一想:
还有其它的列法吗?试说明原因.
(20-x)(32-2x)=570
32-2x
20-x
32
20
观察与思考
方程①、②都不是一元一次方程.那么这两个方程与一元一次方程的区别在哪里?它们有什么共同特点呢?
特点:
①都是整式方程;
②只含一个未知数;
③未知数的最高次数是2.
x2-36x+35=0 ②
只含有一个未知数x,并且未知数的最高次数是2的整式方程,叫做一元二次方程.
任何一个关于x的一元二次方程,经过整理都可以化为 ax2+bx +c = 0(a , b , c为常数, a≠0)
ax2 称为二次项, a 称为二次项系数.
bx 称为一次项, b 称为一次项系数.
c 称为常数项.
思考:为什么要限制a≠0,b,c可以为零吗
知识要点
一元二次方程的概念
一元二次方程的一般形式是
典例精析
例1 下列选项中,关于x的一元二次方程的是( )
C
不是整式方程
含两个未知数
化简整理成
x2-3x+2=0
少了限制条件
a≠0
提示
判断一个方程是不是一元二次方程,首先看是不是整式方程;如是再进一步化简整理后再作判断.
例2:将方程3x(x-1)=5(x+2)化为一般形式,并分别指出它们的二次项、一次项和常数项及它们的系数.
解:
去括号,得
3x2-3x=5x+10.
移项、合并同类项,得一元二次方程的一般形式
3x2-8x-10=0.
其中二次项是3x2,系数是3;一次项是-8x,系数是-8;常数项是-10.
系数和项均包含前面的符号.
注意
一元二次方程的根
二
一元二次方程的根
使一元二次方程等号两边相等的未知数的值叫作一元二次方程的解(又叫做根).
例3:下面哪些数是方程 x2 – x – 6 = 0 的解
-4 ,-3 , -2 ,-1 ,0 ,1,2,3 ,4
解:
3和-2.
你注意到了吗?一元二次方程可能不止一个根.
当堂练习
1. 下列哪些是一元二次方程?如果是一元二次方程,化为一般式:
√
×
√
×
×
√
3x+2=5x-2
x2=0
(x+3)(2x-4)=x2
3y2=(3y+1)(y-2)
x2=x3+x2-1
3x2=5x-1
(1)
(4)
(2)
(3)
(6)
(5)
2.填空:
方程 一般形式 二次项系数 一次项系数 常数项
-2
1
3
1
3
-5
4
0
-5
3
-2
课堂小结
一元二次方程
概念
是整式方程;
含一个未知数;
最高次数是2.
一般形式
ax2+bx+c=0 (a ≠0)
其中(a≠0)是一元二次方程的必要条件;
根
使方程左右两边相等的未知数的值.
谢 谢
