冀教版数学七年级下册 第七章 相交线与平行线 复习课件(共20张PPT)
文档属性
| 名称 | 冀教版数学七年级下册 第七章 相交线与平行线 复习课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 324.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 19:27:06 | ||
图片预览






文档简介
(共20张PPT)
第七章 相交线与平行线 复习课件
知识结构
相交线
两条
直线
相交
邻补角、对顶角
对顶角相等
垂线及其性质
点到直线的距离
两条
直线
被第
三条
直线
所截
同位角、内错角、同旁内角
平行线
平行公理
平移
判定
性质
每个命题都由条件和结论两部分组成。条件是已知事项,结论是由已事项推断出的事项。
一般地,命题可以写成“如果……,那么……”的形式,其中“如果”引出的部分是条件,“那么”引出的部分是结论。
正确的命题称为真命题不正确的的命题称为假命题
要说明一个命题是假命题,通常可以举出一个例子,使之具备命题的条件,而不具备命题的结论,这种例子称为反例
定义:对名称和术语的含义加以描述,作出明确
的规定,也就是给出它们的定义。
命题:判断一件事情的句子,叫做命题
知多少
公理:公认的真命题称为公理(axiom)。
证明:除了公理外,其它真命题的正确性都通过推理
的方法证实。推理的过程称为证明。
定理:经过证明的真命题称为定理(theorem)。
本套教材选用如下命题作为公理:
1.两直线被第三条直线所截,如果同位角相等,
那么这两条直线平行;
2.两条平行线被第三条直线所截,同位角相等;
3.两边及夹角对应相等的两个三角形全等;
4.两角及其夹边对应相等的两个三角形全等;
5.三边对应相等的两个三角形全等;
6.全等三角形的对应边相等,对应角相等。
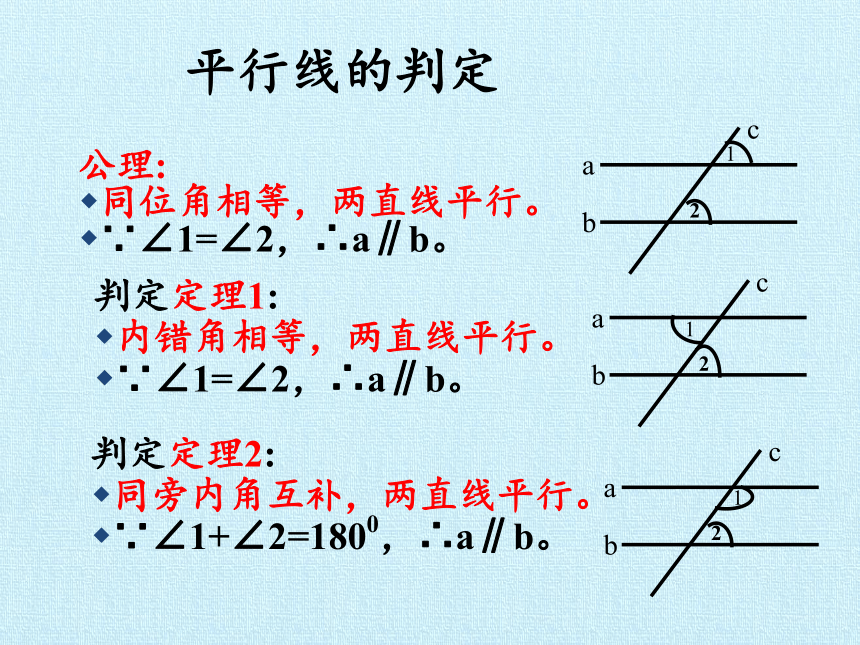
平行线的判定
公理:
同位角相等,两直线平行。
∵∠1=∠2,∴a∥b。
判定定理1:
内错角相等,两直线平行。
∵∠1=∠2,∴a∥b。
判定定理2:
同旁内角互补,两直线平行。
∵∠1+∠2=1800,∴a∥b。
a
b
c
2
1
a
b
c
1
2
a
b
c
1
2
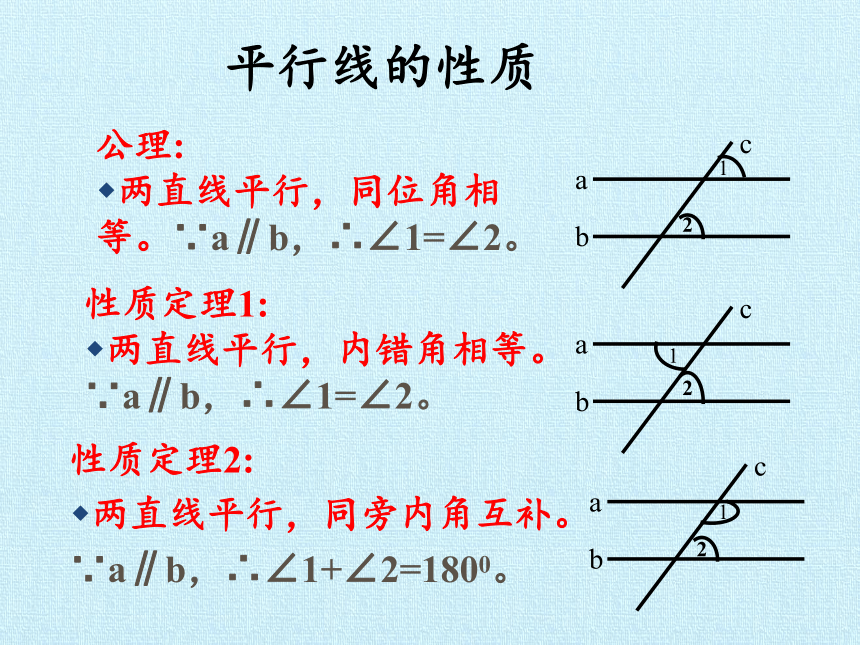
公理:
两直线平行,同位角相等。∵a∥b,∴∠1=∠2。
性质定理1:
两直线平行,内错角相等。
∵a∥b,∴∠1=∠2。
性质定理2:
两直线平行,同旁内角互补。
∵a∥b,∴∠1+∠2=1800。
a
b
c
2
1
a
b
c
1
2
a
b
c
1
2
平行线的性质
三角形内角和定理
三角形内角和定理三角形三个内角的和等于1800。
△ABC中,∠A+∠B+∠C=1800。
∠A+∠B+∠C=1800的几种变形:
∠A=1800–(∠B+∠C)。
∠B=1800–(∠A+∠C)。
∠C=1800–(∠A+∠B)。
∠A+∠B=1800-∠C。
∠B+∠C=1800-∠A。
∠A+∠C=1800-∠B。
这里的结论,以后可以直接运用。
A
B
C
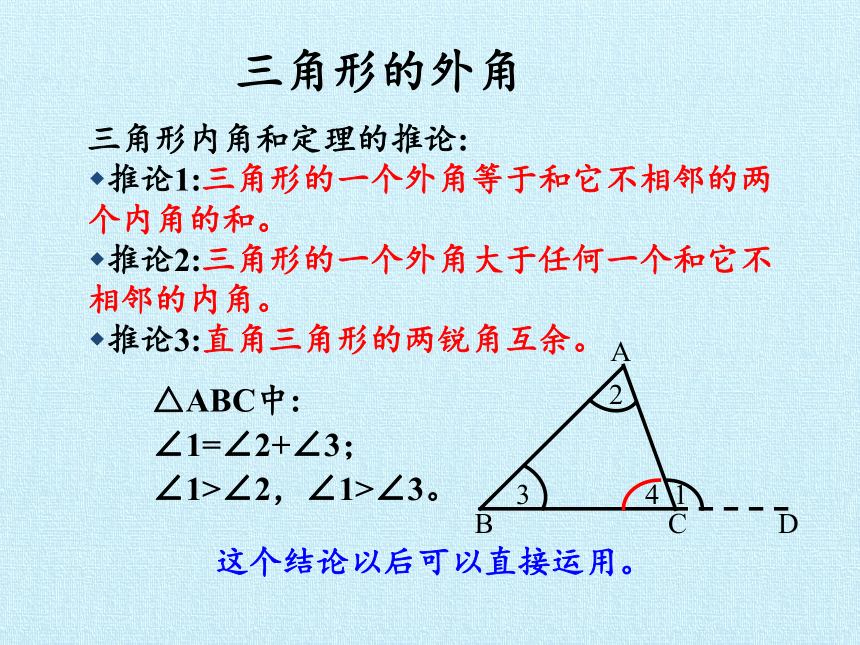
三角形的外角
三角形内角和定理的推论:
推论1:三角形的一个外角等于和它不相邻的两个内角的和。
推论2:三角形的一个外角大于任何一个和它不相邻的内角。
推论3:直角三角形的两锐角互余。
△ABC中:
∠1=∠2+∠3;
∠1>∠2,∠1>∠3。
A
B
C
D
1
2
3
4
这个结论以后可以直接运用。
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证;
(4)分析证明思路,写出证明过程。
如图:∠1是△ABC的一个外角,∠1与图中的
其它角有什么关系?
∠1+∠4=1800;
∠1>∠2;
∠1>∠3;
∠1=∠2+∠3。
证明:∵∠2+∠3+∠4=1800(三角形内角和定理),
∠1+∠4=1800(平角的意义),
∴∠1=∠2+∠3。(等量代换)。
∴∠1>∠2,∠1>∠3(和大于部分)。
A
B
C
D
1
2
3
4
能证明你的结论吗?
用文字表述为:
三角形的一个外角等于和它不相邻的两个内角的和。
三角形的一个外角大于任何一个和它不相邻的内角。
探索思考
外角的内涵与外延
在这里,我们通过三角形内角和定理直接推导出两个新定理。像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论。
推论可以当作定理使用。
三角形内角和定理的推论:
推论1:三角形的一个外角等于和它不相邻的两个内角的和。
推论2:三角形的一个外角大于任何一个和它不相邻的内角。
A
B
C
D
1
2
3
4
例1:已知:如图6-13,在△ABC中,AD平分外角∠EAC,∠B=∠C。
求证:AD∥BC。
A
C
D
B
E
分析:要证明AD∥BC,只需要证明“同位角相等”,“内错角相等”或“同旁内角互补”。
·
·
例题赏析
例2.已知:如图所示,在△ABC中,外角∠DCA=100°,
∠A=45°
求:∠B和∠ACB的大小。
A
B
C
D
解:∵∠DCA是△ABC的一个外角(已知)
∠DCA=100°(已知),
∴∠B=100°-45°=55°。(三角形的一个外角等于和它不相邻的两个内角的和)。
又∵∠DCA+∠BCA=180°(平角意义)。
∴∠ACB=80°(等式的性质)。
∠A=45°(已知),
例题赏析
证明(1):∵ ∠BDC是△DCE的一个外角(外角意义),
∴∠BDC>∠CED(三角形的一个外角大于和它不相邻的任何一个外角)。
∴∠DEC>∠A(三角形的一个外角大于和它不相邻的任何一个外角)。
∴∠BDC>∠A(不等式的性质)。
∵∠DEC是△ABE的一个外角(外角意义),
例3:已知:如图所示。
求证:(1)∠BDC>∠A;
(2)∠BDC=∠A+∠B+∠C。
B
C
A
D
E
例题赏析
证明(2):∵∠BDC是△DCE的一个外角(外角意义),
∴∠BDC=∠C+∠CED(三角形的一个外角等于和它不相邻的两个内角的和)。
∴∠DEC=∠A+∠B(三角形的一个外角等于和它不相邻的两个外角的和)。
∴∠BDC=∠A+∠B+∠C(等式的性质)。
∵∠DEC是△ABE的一个外角(外角意义),
B
C
A
D
E
1.如图:将正方形的四个顶点用线段连接,什么样的线段最短?研究发现,并非对角线最短,而是如图所示的连法最短(即用线段AE,DE,EF,BF,CF把四个顶点连接起来)。
已知图中∠DAE=∠ADE=300,∠AEF=∠BFE=1200。你能证明此时的AB∥EF吗?
A
B
C
D
1题图
E
F
课堂练习
2.已知:如图,直线a,b被直线c所截,a∥b。
求证:∠1+∠2=1800。
b
a
c
2
1
2题图
∴∠2+∠4=1800(两直线平行,同旁内角互补)
证明1:∵a∥b(已知)
∴∠2=∠3(两直线平行,内错角相等)
又∵∠1+∠3=1800(平角意义)
∴∠1+∠2=1800(等量代换)
证明2:∵a∥b(已知)
∠1=∠4(对顶角相等)
∴∠1+∠2=1800(等量代换)
b
a
c
2
1
2题图
3
4
3.已知:如图,∠1+∠2=1800。
求证:∠3=∠4。
分析:要证明∠3=∠4,只要证明CD∥EF;而由∠1+∠2=1800,可得∠1+∠5=1800。从而可得CD∥EF
4
1
2
3
O
C
E
A
B
F
D
3题图
5
谢 谢
第七章 相交线与平行线 复习课件
知识结构
相交线
两条
直线
相交
邻补角、对顶角
对顶角相等
垂线及其性质
点到直线的距离
两条
直线
被第
三条
直线
所截
同位角、内错角、同旁内角
平行线
平行公理
平移
判定
性质
每个命题都由条件和结论两部分组成。条件是已知事项,结论是由已事项推断出的事项。
一般地,命题可以写成“如果……,那么……”的形式,其中“如果”引出的部分是条件,“那么”引出的部分是结论。
正确的命题称为真命题不正确的的命题称为假命题
要说明一个命题是假命题,通常可以举出一个例子,使之具备命题的条件,而不具备命题的结论,这种例子称为反例
定义:对名称和术语的含义加以描述,作出明确
的规定,也就是给出它们的定义。
命题:判断一件事情的句子,叫做命题
知多少
公理:公认的真命题称为公理(axiom)。
证明:除了公理外,其它真命题的正确性都通过推理
的方法证实。推理的过程称为证明。
定理:经过证明的真命题称为定理(theorem)。
本套教材选用如下命题作为公理:
1.两直线被第三条直线所截,如果同位角相等,
那么这两条直线平行;
2.两条平行线被第三条直线所截,同位角相等;
3.两边及夹角对应相等的两个三角形全等;
4.两角及其夹边对应相等的两个三角形全等;
5.三边对应相等的两个三角形全等;
6.全等三角形的对应边相等,对应角相等。
平行线的判定
公理:
同位角相等,两直线平行。
∵∠1=∠2,∴a∥b。
判定定理1:
内错角相等,两直线平行。
∵∠1=∠2,∴a∥b。
判定定理2:
同旁内角互补,两直线平行。
∵∠1+∠2=1800,∴a∥b。
a
b
c
2
1
a
b
c
1
2
a
b
c
1
2
公理:
两直线平行,同位角相等。∵a∥b,∴∠1=∠2。
性质定理1:
两直线平行,内错角相等。
∵a∥b,∴∠1=∠2。
性质定理2:
两直线平行,同旁内角互补。
∵a∥b,∴∠1+∠2=1800。
a
b
c
2
1
a
b
c
1
2
a
b
c
1
2
平行线的性质
三角形内角和定理
三角形内角和定理三角形三个内角的和等于1800。
△ABC中,∠A+∠B+∠C=1800。
∠A+∠B+∠C=1800的几种变形:
∠A=1800–(∠B+∠C)。
∠B=1800–(∠A+∠C)。
∠C=1800–(∠A+∠B)。
∠A+∠B=1800-∠C。
∠B+∠C=1800-∠A。
∠A+∠C=1800-∠B。
这里的结论,以后可以直接运用。
A
B
C
三角形的外角
三角形内角和定理的推论:
推论1:三角形的一个外角等于和它不相邻的两个内角的和。
推论2:三角形的一个外角大于任何一个和它不相邻的内角。
推论3:直角三角形的两锐角互余。
△ABC中:
∠1=∠2+∠3;
∠1>∠2,∠1>∠3。
A
B
C
D
1
2
3
4
这个结论以后可以直接运用。
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证;
(4)分析证明思路,写出证明过程。
如图:∠1是△ABC的一个外角,∠1与图中的
其它角有什么关系?
∠1+∠4=1800;
∠1>∠2;
∠1>∠3;
∠1=∠2+∠3。
证明:∵∠2+∠3+∠4=1800(三角形内角和定理),
∠1+∠4=1800(平角的意义),
∴∠1=∠2+∠3。(等量代换)。
∴∠1>∠2,∠1>∠3(和大于部分)。
A
B
C
D
1
2
3
4
能证明你的结论吗?
用文字表述为:
三角形的一个外角等于和它不相邻的两个内角的和。
三角形的一个外角大于任何一个和它不相邻的内角。
探索思考
外角的内涵与外延
在这里,我们通过三角形内角和定理直接推导出两个新定理。像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论。
推论可以当作定理使用。
三角形内角和定理的推论:
推论1:三角形的一个外角等于和它不相邻的两个内角的和。
推论2:三角形的一个外角大于任何一个和它不相邻的内角。
A
B
C
D
1
2
3
4
例1:已知:如图6-13,在△ABC中,AD平分外角∠EAC,∠B=∠C。
求证:AD∥BC。
A
C
D
B
E
分析:要证明AD∥BC,只需要证明“同位角相等”,“内错角相等”或“同旁内角互补”。
·
·
例题赏析
例2.已知:如图所示,在△ABC中,外角∠DCA=100°,
∠A=45°
求:∠B和∠ACB的大小。
A
B
C
D
解:∵∠DCA是△ABC的一个外角(已知)
∠DCA=100°(已知),
∴∠B=100°-45°=55°。(三角形的一个外角等于和它不相邻的两个内角的和)。
又∵∠DCA+∠BCA=180°(平角意义)。
∴∠ACB=80°(等式的性质)。
∠A=45°(已知),
例题赏析
证明(1):∵ ∠BDC是△DCE的一个外角(外角意义),
∴∠BDC>∠CED(三角形的一个外角大于和它不相邻的任何一个外角)。
∴∠DEC>∠A(三角形的一个外角大于和它不相邻的任何一个外角)。
∴∠BDC>∠A(不等式的性质)。
∵∠DEC是△ABE的一个外角(外角意义),
例3:已知:如图所示。
求证:(1)∠BDC>∠A;
(2)∠BDC=∠A+∠B+∠C。
B
C
A
D
E
例题赏析
证明(2):∵∠BDC是△DCE的一个外角(外角意义),
∴∠BDC=∠C+∠CED(三角形的一个外角等于和它不相邻的两个内角的和)。
∴∠DEC=∠A+∠B(三角形的一个外角等于和它不相邻的两个外角的和)。
∴∠BDC=∠A+∠B+∠C(等式的性质)。
∵∠DEC是△ABE的一个外角(外角意义),
B
C
A
D
E
1.如图:将正方形的四个顶点用线段连接,什么样的线段最短?研究发现,并非对角线最短,而是如图所示的连法最短(即用线段AE,DE,EF,BF,CF把四个顶点连接起来)。
已知图中∠DAE=∠ADE=300,∠AEF=∠BFE=1200。你能证明此时的AB∥EF吗?
A
B
C
D
1题图
E
F
课堂练习
2.已知:如图,直线a,b被直线c所截,a∥b。
求证:∠1+∠2=1800。
b
a
c
2
1
2题图
∴∠2+∠4=1800(两直线平行,同旁内角互补)
证明1:∵a∥b(已知)
∴∠2=∠3(两直线平行,内错角相等)
又∵∠1+∠3=1800(平角意义)
∴∠1+∠2=1800(等量代换)
证明2:∵a∥b(已知)
∠1=∠4(对顶角相等)
∴∠1+∠2=1800(等量代换)
b
a
c
2
1
2题图
3
4
3.已知:如图,∠1+∠2=1800。
求证:∠3=∠4。
分析:要证明∠3=∠4,只要证明CD∥EF;而由∠1+∠2=1800,可得∠1+∠5=1800。从而可得CD∥EF
4
1
2
3
O
C
E
A
B
F
D
3题图
5
谢 谢
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
