小学数学人教版六年级下正比例 表格式教学设计
文档属性
| 名称 | 小学数学人教版六年级下正比例 表格式教学设计 |
|
|
| 格式 | docx | ||
| 文件大小 | 910.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 17:22:16 | ||
图片预览


文档简介
《正比例》
教学目标:
理解正比例的意义,能根据意义判断两种量是否成正比例关系。认识正比例图象 。
在观察、比较、交流等学习过程中,培养抽象意识和概括分析能力,渗透模型、函数以及数形结合思想。
感受数学知识间的联系,体会数学的价值。
教学重点:理解正比例的意义
教学难点:根据意义判断两种量是否成正比例关系
教学准备:学习单、课件
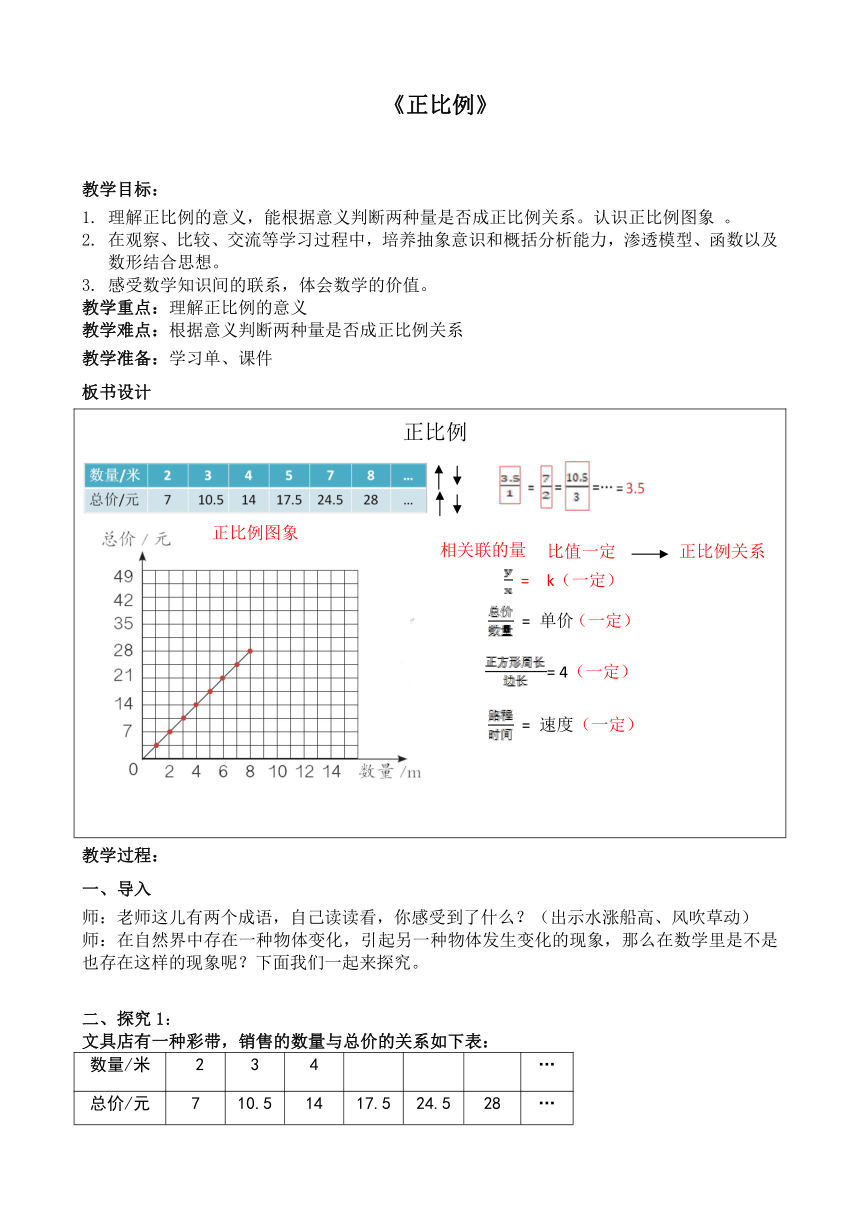
板书设计
正比例 (
正比例图象
) (
正比例关系
) (
相关联的量
) (
= k(一定)
) (
= 速度
(一定)
) (
=
4
(一定)
) (
=
单价
(一定)
) (
比值一定
) (
)
教学过程:
一、导入
师:老师这儿有两个成语,自己读读看,你感受到了什么?(出示水涨船高、风吹草动)
师:在自然界中存在一种物体变化,引起另一种物体发生变化的现象,那么在数学里是不是也存在这样的现象呢?下面我们一起来探究。
二、探究1:
文具店有一种彩带,销售的数量与总价的关系如下表:
数量/米 2 3 4 …
总价/元 7 10.5 14 17.5 24.5 28 …
请你把表格填写完整。 观察表格,你发现了什么? 3.利用表格中的数据用图象表示总价和数量的关系。 (
探究1:
(1)、师:看到探究1,请你在学习单上先完成第1和第2小题。
反馈
师:先请同学来说一说你是怎么填写表格的?
师:你在填表的过程中,你又发现了什么呢?
预设:
a、总价随数量的增加而增加,随数量的减少而减少
师:你是从什么方向观察得到的?
b、单价不变,都是3.5元。
师:你是怎么知道单价是不变的?
师:你能用个式子来表示总价、数量的关系吗?
师:同学们真会观察,无论是横着观察,还是竖着观察,都能找到总价和数量的关联。
师:像这样,我们说总价和数量就是成正比例关系。
师:今天,我们就是来研究正比例。
(2)、师:其实这两个量成正比例关系,表中的这些数据还可以用图象表示。 (师介绍画法,生尝试)
反馈
师:
这两位同学画的图象有什么共同点?(直的线)
师:又有什么不同点呢?(有长短)
师:这条线可以延长吗?
师:我们延长后,在延长线上的取这两个点也符合单价是3.5元,比值一定的要求吗?
师:所以啊,这条线上所有的点都具有什么共同点?(比值一定)
师:既然两端可以延伸,这端可以延伸至哪个点?(0,0)表示什么意思?
师:这个图象就是
正比例图象。
是一条从(
0,0
)出发
的一条直的线。
(3)、师:学到这里,你认为当总价和数量怎么样时才可以说成正比例关系呢?
(预设:a、总价随数量的增加而增加,随数量的减少而减少;b、总价比数量,单价一定;c、图象是一条从(0,0)出发的直的线。)
)
三、探究2: 任选其中一个材料,用你的方法判断相应材料中的两个量是否成正比例关系。
材料一: 边长/厘米1234…周长/厘米…
边长/厘米1234…面积/平方厘米…
1、请填写两张表格,计算正方形的周长和面积。 2、观察表格,请你用自己的方法判断出表格中哪两种量成正比例关系。 材料二: 汽车行驶的路程和时间如下表: 时间/时 1 2 3 4 5 … 路程/千米 80 160 240 320 400 …
路程和时间成正比关系吗?用自己的方法说明。 (
探究2:
(
1
)、师:
其他还有哪些量也是成正比例关系呢,我们一起来探究。
老师给大家准备了两个材料,请你任选其中一个材料,用你的方法判断相应材料中的两个量是否成正比例关系。
材料1:
师:你们看这位同学写的,得出周长和边长成正比例关系,面积和边长不成正比例关系,真的是这样的吗?谁来说你的想法?
师:你能用一个式子表示出周长和边长的数量关系吗?
师:还有想补充的吗?
师:对啊,从图像也能判断,周长和边长的关系图像是一条从(0,0)出发的直直的线,而面积和边长的关系图像,则是一条曲线。
师:所以说,面积和边长光是变化同步,有关联还不够,未必是成正比例关系,还得满足什么要求?
材料2:
展示求比值和画图象两种方法。
(2)、师;同学们,现在你们认为成正比例关系的两个量需要符合哪些要求?
(预设:比值一定,相关联,图象是直的线)
师:我们说如果两个量是相关联的量,且它们的比值一定,那这两个量就是成正比例关系。(板书)
师:像黑板上的这些式子,都是两两相关联,且它们的比值一定,所以里面的两个量是成正比例关系。
师:如果我们用一个字母式子来表示它们的正比例关系,你会想到什么式子?
师:在数学中,我们习惯用字母y和x表示两个相关联的量,用k表示它们的比值,比值一定,这就是表示正比例关系的式子。这些式子都能用这个字母式子来表示。
)
四、 巩固练习
练习1:判断下面每题中的两种量是否成正比例关系,并说明理由。 1、圆的周长与它的直径。 2、书的总页数一定,已读的页数与未读的页数。 3、工作总量一定,工作效率和工作时间。 (
练习1:
预设:
举例子,求比值;
数量关系式
师:同学们,在刚才的练习中,你们大致用到了几种判断两种量是否成正比例关系方法?
师:还可以根据给出的两种量想它们的数量关系式,再根据式子判断它们的比值是否一定。
)
练习2: 面批: (
练习
2:
正比例图象的应用
会判断正比例关系
概括出正比例字母关系式
)
教学目标:
理解正比例的意义,能根据意义判断两种量是否成正比例关系。认识正比例图象 。
在观察、比较、交流等学习过程中,培养抽象意识和概括分析能力,渗透模型、函数以及数形结合思想。
感受数学知识间的联系,体会数学的价值。
教学重点:理解正比例的意义
教学难点:根据意义判断两种量是否成正比例关系
教学准备:学习单、课件
板书设计
正比例 (
正比例图象
) (
正比例关系
) (
相关联的量
) (
= k(一定)
) (
= 速度
(一定)
) (
=
4
(一定)
) (
=
单价
(一定)
) (
比值一定
) (
)
教学过程:
一、导入
师:老师这儿有两个成语,自己读读看,你感受到了什么?(出示水涨船高、风吹草动)
师:在自然界中存在一种物体变化,引起另一种物体发生变化的现象,那么在数学里是不是也存在这样的现象呢?下面我们一起来探究。
二、探究1:
文具店有一种彩带,销售的数量与总价的关系如下表:
数量/米 2 3 4 …
总价/元 7 10.5 14 17.5 24.5 28 …
请你把表格填写完整。 观察表格,你发现了什么? 3.利用表格中的数据用图象表示总价和数量的关系。 (
探究1:
(1)、师:看到探究1,请你在学习单上先完成第1和第2小题。
反馈
师:先请同学来说一说你是怎么填写表格的?
师:你在填表的过程中,你又发现了什么呢?
预设:
a、总价随数量的增加而增加,随数量的减少而减少
师:你是从什么方向观察得到的?
b、单价不变,都是3.5元。
师:你是怎么知道单价是不变的?
师:你能用个式子来表示总价、数量的关系吗?
师:同学们真会观察,无论是横着观察,还是竖着观察,都能找到总价和数量的关联。
师:像这样,我们说总价和数量就是成正比例关系。
师:今天,我们就是来研究正比例。
(2)、师:其实这两个量成正比例关系,表中的这些数据还可以用图象表示。 (师介绍画法,生尝试)
反馈
师:
这两位同学画的图象有什么共同点?(直的线)
师:又有什么不同点呢?(有长短)
师:这条线可以延长吗?
师:我们延长后,在延长线上的取这两个点也符合单价是3.5元,比值一定的要求吗?
师:所以啊,这条线上所有的点都具有什么共同点?(比值一定)
师:既然两端可以延伸,这端可以延伸至哪个点?(0,0)表示什么意思?
师:这个图象就是
正比例图象。
是一条从(
0,0
)出发
的一条直的线。
(3)、师:学到这里,你认为当总价和数量怎么样时才可以说成正比例关系呢?
(预设:a、总价随数量的增加而增加,随数量的减少而减少;b、总价比数量,单价一定;c、图象是一条从(0,0)出发的直的线。)
)
三、探究2: 任选其中一个材料,用你的方法判断相应材料中的两个量是否成正比例关系。
材料一: 边长/厘米1234…周长/厘米…
边长/厘米1234…面积/平方厘米…
1、请填写两张表格,计算正方形的周长和面积。 2、观察表格,请你用自己的方法判断出表格中哪两种量成正比例关系。 材料二: 汽车行驶的路程和时间如下表: 时间/时 1 2 3 4 5 … 路程/千米 80 160 240 320 400 …
路程和时间成正比关系吗?用自己的方法说明。 (
探究2:
(
1
)、师:
其他还有哪些量也是成正比例关系呢,我们一起来探究。
老师给大家准备了两个材料,请你任选其中一个材料,用你的方法判断相应材料中的两个量是否成正比例关系。
材料1:
师:你们看这位同学写的,得出周长和边长成正比例关系,面积和边长不成正比例关系,真的是这样的吗?谁来说你的想法?
师:你能用一个式子表示出周长和边长的数量关系吗?
师:还有想补充的吗?
师:对啊,从图像也能判断,周长和边长的关系图像是一条从(0,0)出发的直直的线,而面积和边长的关系图像,则是一条曲线。
师:所以说,面积和边长光是变化同步,有关联还不够,未必是成正比例关系,还得满足什么要求?
材料2:
展示求比值和画图象两种方法。
(2)、师;同学们,现在你们认为成正比例关系的两个量需要符合哪些要求?
(预设:比值一定,相关联,图象是直的线)
师:我们说如果两个量是相关联的量,且它们的比值一定,那这两个量就是成正比例关系。(板书)
师:像黑板上的这些式子,都是两两相关联,且它们的比值一定,所以里面的两个量是成正比例关系。
师:如果我们用一个字母式子来表示它们的正比例关系,你会想到什么式子?
师:在数学中,我们习惯用字母y和x表示两个相关联的量,用k表示它们的比值,比值一定,这就是表示正比例关系的式子。这些式子都能用这个字母式子来表示。
)
四、 巩固练习
练习1:判断下面每题中的两种量是否成正比例关系,并说明理由。 1、圆的周长与它的直径。 2、书的总页数一定,已读的页数与未读的页数。 3、工作总量一定,工作效率和工作时间。 (
练习1:
预设:
举例子,求比值;
数量关系式
师:同学们,在刚才的练习中,你们大致用到了几种判断两种量是否成正比例关系方法?
师:还可以根据给出的两种量想它们的数量关系式,再根据式子判断它们的比值是否一定。
)
练习2: 面批: (
练习
2:
正比例图象的应用
会判断正比例关系
概括出正比例字母关系式
)
