1.3.2杨辉三角与二项式系数的性质课件 新人教A版选修2
文档属性
| 名称 | 1.3.2杨辉三角与二项式系数的性质课件 新人教A版选修2 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-08 00:00:00 | ||
图片预览







文档简介
课件20张PPT。1.3.2“杨辉三角”与二项式系数的性质复习回顾二项展开式中的二项式系数指的是那些?共有多少个? 下面我们来研究二项式系数有些什么性质?我们先通过杨辉三角观察n为特殊值时,二项式系数有什么特点?1.“杨辉三角”的来历及规律 杨辉三角展开式中的二项式系数,如下表所示: 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 …… …… ……观察二项式系数表,寻求其规律: 不难发现,表中每行两端都是1,而且除1以外的每一个数都等于它肩上两个数的和.事实上,设表中任一不为1的数为Cn+1r,那么它肩上的两个数分别为Cnr-1及Cnr,知道Cn+1r = Cnr-1+Cnr 这就是组合数的性质2.(1)对称性:
与首末两端“等距离”的两个二项式系数相等.(a+b)n展开式的二项式系数依次是: (3)增减性与最大值. (2)递推性:
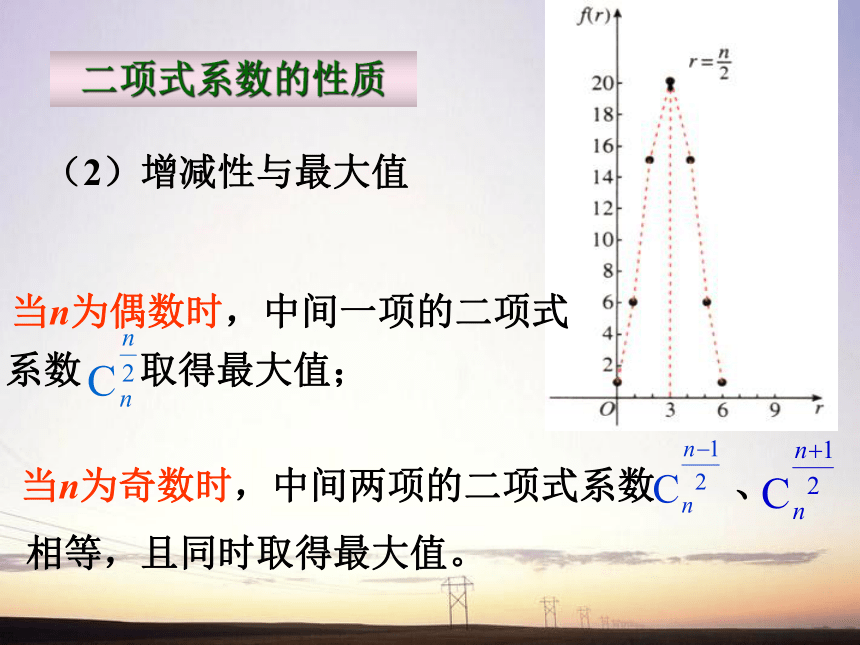
除1以外的每一个数都等于它肩上两个数的和.(4)各二项式系数的和. 当n为偶数时,中间一项取得最大项;
当n为奇数时,中间两项同时取得最大值。
可运用函数的观点,结合“杨辉三角”和函数图象,研究二项式系数的性质. (a+b)n展开式的二项式系数是
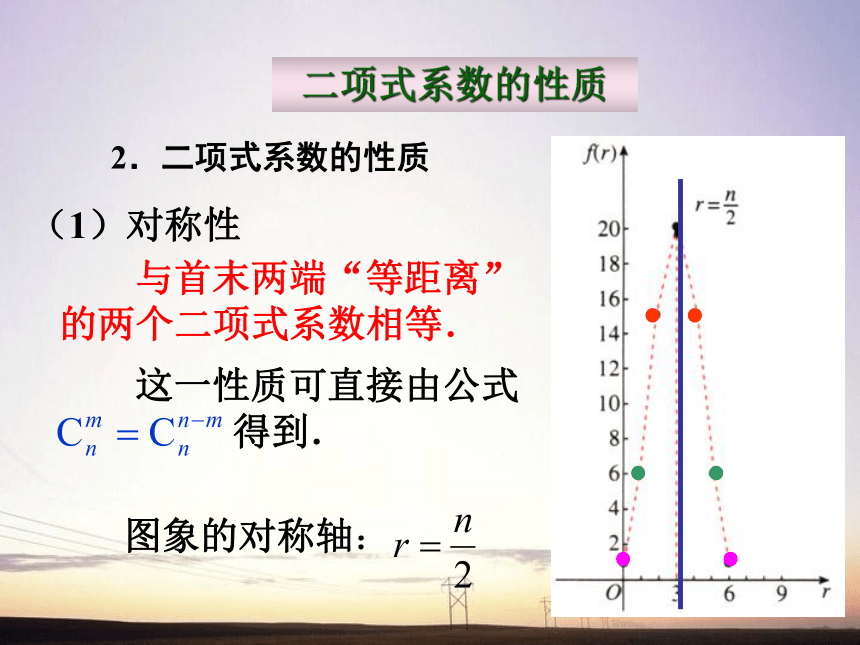
可看成是以r为自变量的函数f(r),其定义域是{0,1,2,…,n},当n=6时,其图象是右图中的7个孤立点.二项式系数的性质2.二项式系数的性质 (1)对称性 与首末两端“等距离”的两个二项式系数相等. 这一性质可直接由公式
得到.图象的对称轴:二项式系数的性质(2)增减性与最大值 (3)各二项式系数的和 二项式系数的性质在二项式定理中,令 ,则: 这就是说, 的展开式的各二项式系数的和等于:同时由于 ,上式还可以写成: 启示:在二项式定理中,对a,b赋予一些特定的值,是解决二项式有关问题的一种重要方法——赋值法。继续思考:
试证明在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.即证:证明:在展开式 中
令a=1,b=-1得 启示:在二项式定理中,对a,b赋予一些特定的值,是解决二项式有关问题的一种重要方法——赋值法。结束思考2求证:略证:由(1+x)n(1+x)n=(1+x)2n,两边展开后比较xn的系数得:
再由 得
课堂练习:
1)已知 ,那么 = ;
2) 的展开式中,二项式系数的最大值是 ;
3)若 的展开式中的第十项和第十一项的二项式系数最大,则n= ; 例1 证明在 的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和. 例3: 的展开式中第6项与第7项的系数相等,求展开式中二项式系数最大的项和系数最大的项。变式引申:
1、 的展开式中,系数绝对值最大的项是( )
A.第4项 B.第4、5项 C.第5项 D.第3、4项
2、若 展开式中的第6项的系数最大,则不含x的项等于( )
A.210 B.120 C.461 D.416例4、若 展开式中前三项系数成等差
数列,求(1)展开式中含x的一次幂的项;
(2)展开式中所有x 的有理项;
(3)展开式中系数最大的项。1、已知 的展开式中x3的系数
为 ,则常数a的值是_______ 2、在(1-x3)(1+x)10的展开式中x5的系数是( )
A.-297 B.-252 C. 297 D. 2073、(x+y+z)9中含x4y2z3的项的系数是__________课堂练习4.已知(1+ )n展开式中含x-2的项的系数为12,求n.
5.已知(10+xlgx)5的展开式中第4项为106,求x的值. 二项展开式中的二项式系数都是一些特殊的组合数,它有三条性质,要理解和掌握好,同时要注意“系数”与“二项式系数”的区别,不能混淆,只有二项式系数最大的才是中间项,而系数最大的不一定是中间项,尤其要理解和掌握“取特值”法,它是解决有关二项展开式系数的问题的重要手段。小结二项式系数的性质(2)增减性与最大值 由于:所以 相对于 的增减情况由 决定. 二项式系数的性质(2)增减性与最大值 由: 二项式系数是逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值。 可知,当 时,
与首末两端“等距离”的两个二项式系数相等.(a+b)n展开式的二项式系数依次是: (3)增减性与最大值. (2)递推性:
除1以外的每一个数都等于它肩上两个数的和.(4)各二项式系数的和. 当n为偶数时,中间一项取得最大项;
当n为奇数时,中间两项同时取得最大值。
可运用函数的观点,结合“杨辉三角”和函数图象,研究二项式系数的性质. (a+b)n展开式的二项式系数是
可看成是以r为自变量的函数f(r),其定义域是{0,1,2,…,n},当n=6时,其图象是右图中的7个孤立点.二项式系数的性质2.二项式系数的性质 (1)对称性 与首末两端“等距离”的两个二项式系数相等. 这一性质可直接由公式
得到.图象的对称轴:二项式系数的性质(2)增减性与最大值 (3)各二项式系数的和 二项式系数的性质在二项式定理中,令 ,则: 这就是说, 的展开式的各二项式系数的和等于:同时由于 ,上式还可以写成: 启示:在二项式定理中,对a,b赋予一些特定的值,是解决二项式有关问题的一种重要方法——赋值法。继续思考:
试证明在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.即证:证明:在展开式 中
令a=1,b=-1得 启示:在二项式定理中,对a,b赋予一些特定的值,是解决二项式有关问题的一种重要方法——赋值法。结束思考2求证:略证:由(1+x)n(1+x)n=(1+x)2n,两边展开后比较xn的系数得:
再由 得
课堂练习:
1)已知 ,那么 = ;
2) 的展开式中,二项式系数的最大值是 ;
3)若 的展开式中的第十项和第十一项的二项式系数最大,则n= ; 例1 证明在 的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和. 例3: 的展开式中第6项与第7项的系数相等,求展开式中二项式系数最大的项和系数最大的项。变式引申:
1、 的展开式中,系数绝对值最大的项是( )
A.第4项 B.第4、5项 C.第5项 D.第3、4项
2、若 展开式中的第6项的系数最大,则不含x的项等于( )
A.210 B.120 C.461 D.416例4、若 展开式中前三项系数成等差
数列,求(1)展开式中含x的一次幂的项;
(2)展开式中所有x 的有理项;
(3)展开式中系数最大的项。1、已知 的展开式中x3的系数
为 ,则常数a的值是_______ 2、在(1-x3)(1+x)10的展开式中x5的系数是( )
A.-297 B.-252 C. 297 D. 2073、(x+y+z)9中含x4y2z3的项的系数是__________课堂练习4.已知(1+ )n展开式中含x-2的项的系数为12,求n.
5.已知(10+xlgx)5的展开式中第4项为106,求x的值. 二项展开式中的二项式系数都是一些特殊的组合数,它有三条性质,要理解和掌握好,同时要注意“系数”与“二项式系数”的区别,不能混淆,只有二项式系数最大的才是中间项,而系数最大的不一定是中间项,尤其要理解和掌握“取特值”法,它是解决有关二项展开式系数的问题的重要手段。小结二项式系数的性质(2)增减性与最大值 由于:所以 相对于 的增减情况由 决定. 二项式系数的性质(2)增减性与最大值 由: 二项式系数是逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值。 可知,当 时,
