湘教版七年级下册 4.6 两条平行线间的距离课件(共15张PPT)
文档属性
| 名称 | 湘教版七年级下册 4.6 两条平行线间的距离课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 344.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 19:29:55 | ||
图片预览





文档简介
(共15张PPT)
1、你的数学课本右上角顶点与左下角顶点的距离是多少?请你量一量。
A
B
右上角顶点和左下
角顶点的距离是点
与点的距离。应测
量线段AB的长度。
梳理旧知,引出新课
2、你的数学课本右上角顶点到下面边缘线的距离是多少?请你量一量。
两点之间的距离是这两点间的线段的长度,点到直线的距离是这点到这条直线的垂线段的长度.
右上角顶点到
下面边缘线的
距离应测量线
段CD的长度。
C
D
3、怎样测量数学课本的宽度呢?
我们先来学习------
动手操作,归纳结论
主题一、 公垂线和公垂线段的概念
A
B
a
b
与两条平行直线都垂直的直线,叫做这两条平行直线的公垂线。
连接两个垂足的线段,叫做这两条平行直线的公垂线段
2、平行线的画法:
·
动手操作,归纳结论
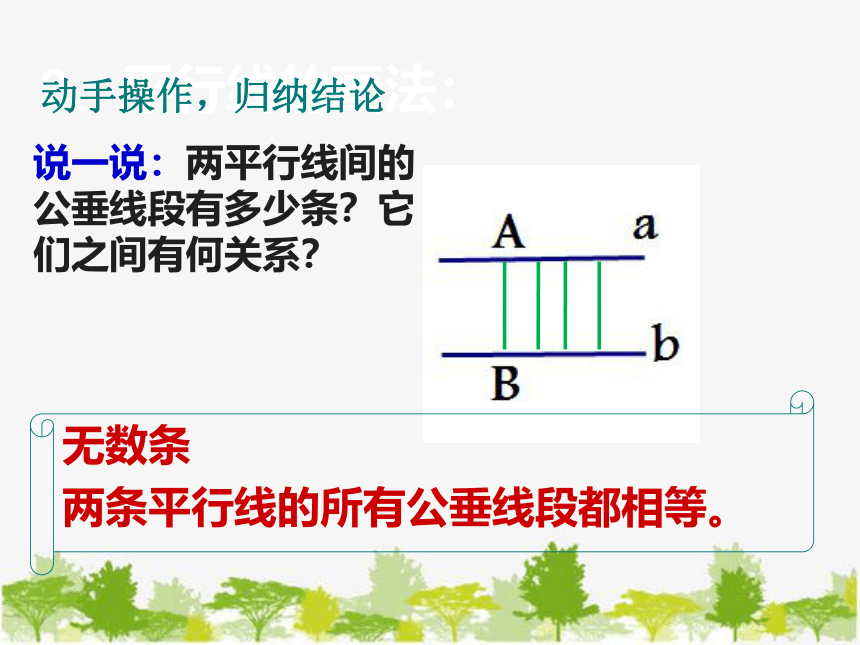
说一说:两平行线间的公垂线段有多少条?它们之间有何关系?
无数条
两条平行线的所有公垂线段都相等。
动手操作,归纳结论
主题二、 两条平行线间的距离
A
B
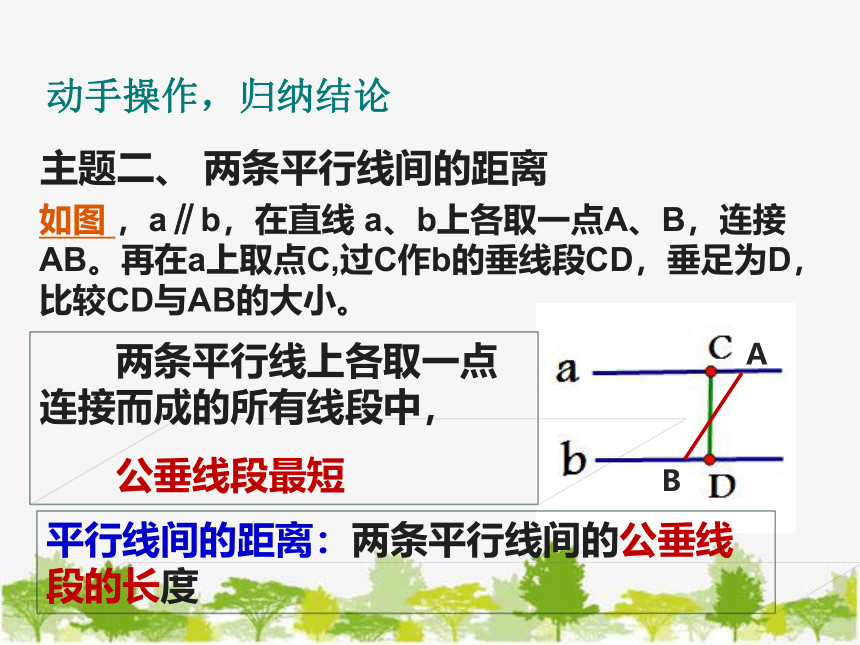
如图 ,a∥b,在直线 a、b上各取一点A、B,连接AB。再在a上取点C,过C作b的垂线段CD,垂足为D,比较CD与AB的大小。
两条平行线上各取一点连接而成的所有线段中,
公垂线段最短
平行线间的距离:两条平行线间的公垂线段的长度
试试看: 1、平行线间的距离是指( ) A 公垂线, B 公垂线段, C 公垂线段的长度, D 以上都不对。
注意:平行线间的距离是指“公垂线段的长度”,而不是“公垂线段”,更不是“公垂线”
C
2、已知AB∥CD,若四条线段PO【答】不对,因为平行线间的距离是两条平
行线之间的公垂线段的长度,而PO虽然是最
短的,但不一定是公垂线段。
应用迁移
1、测量平行线间的距离
请你量出课本的宽度,再与同学交流你的测量方法。
注意:
量测量两条平行线间的距离一定要测量公垂线段的长度。
边缘线是公垂线,
测量图中红色线段
就是书本的宽。
2、 求平行线间的距离 【例】如图设直线a、b、c是三条平行直线。已知a与b的距离为5厘米,b与c的距离为2厘米,求a与c的距离。
【解】在a 上任取一点A, 过A 作AC⊥a,分别与b,c相交于B,C 两点,则AB,BC,AC分别表示a 与b,b与c, a与c的公垂线段.
AC=AB+BC=5+2=7(cm)
因此a与c的距离是7 cm.
【变式练习】设直线a、b、c是三条平行直线。已知a与b的距离为5厘米,b与c的距离为2厘米,则a与c的距离为( ) A、7cm B、3cm
C、7cm或3cm D、以上都不对
【解析】直线c的位置有两种情况:一是如上题图情形,此时a,c的距离是7cm,二是直线c在直线a、b之间,此时a,c之间的距离是3cm.所以选C。
a
b
c
C
a
b
c
课堂练习 1、如图, MN∥AB,P,Q为直线MN 上的任意两点,三角形PAB和三角形QAB的面积有什么关系?为什么?
【解】三角形PAB与三角形QAB的面积相等。
理由:因为MN∥AB,则点P、Q到AB的距离相等,所以三角形PAB与三角形QAB的边AB上的高相等,又边AB公共,所以这两个三角形面积相等。
2、如图的四边形中,∠A=∠B=∠C=∠D=90°,这样的四边形叫做矩形.矩形的两组对边AB和DC,AD和BC相等吗?为什么?
【解】相等,
理由:AD、BC平行,且AB、DC是AD、BC两平行线间的公垂线段,所以AB=DC,同样的道理,AD=BC.
归纳小结:
这节课你有什么收获?
1、什么叫公垂线和公垂线段?
2、两平行线间的距离是指公垂线段的长,是数量,不是图形。
1、你的数学课本右上角顶点与左下角顶点的距离是多少?请你量一量。
A
B
右上角顶点和左下
角顶点的距离是点
与点的距离。应测
量线段AB的长度。
梳理旧知,引出新课
2、你的数学课本右上角顶点到下面边缘线的距离是多少?请你量一量。
两点之间的距离是这两点间的线段的长度,点到直线的距离是这点到这条直线的垂线段的长度.
右上角顶点到
下面边缘线的
距离应测量线
段CD的长度。
C
D
3、怎样测量数学课本的宽度呢?
我们先来学习------
动手操作,归纳结论
主题一、 公垂线和公垂线段的概念
A
B
a
b
与两条平行直线都垂直的直线,叫做这两条平行直线的公垂线。
连接两个垂足的线段,叫做这两条平行直线的公垂线段
2、平行线的画法:
·
动手操作,归纳结论
说一说:两平行线间的公垂线段有多少条?它们之间有何关系?
无数条
两条平行线的所有公垂线段都相等。
动手操作,归纳结论
主题二、 两条平行线间的距离
A
B
如图 ,a∥b,在直线 a、b上各取一点A、B,连接AB。再在a上取点C,过C作b的垂线段CD,垂足为D,比较CD与AB的大小。
两条平行线上各取一点连接而成的所有线段中,
公垂线段最短
平行线间的距离:两条平行线间的公垂线段的长度
试试看: 1、平行线间的距离是指( ) A 公垂线, B 公垂线段, C 公垂线段的长度, D 以上都不对。
注意:平行线间的距离是指“公垂线段的长度”,而不是“公垂线段”,更不是“公垂线”
C
2、已知AB∥CD,若四条线段PO
行线之间的公垂线段的长度,而PO虽然是最
短的,但不一定是公垂线段。
应用迁移
1、测量平行线间的距离
请你量出课本的宽度,再与同学交流你的测量方法。
注意:
量测量两条平行线间的距离一定要测量公垂线段的长度。
边缘线是公垂线,
测量图中红色线段
就是书本的宽。
2、 求平行线间的距离 【例】如图设直线a、b、c是三条平行直线。已知a与b的距离为5厘米,b与c的距离为2厘米,求a与c的距离。
【解】在a 上任取一点A, 过A 作AC⊥a,分别与b,c相交于B,C 两点,则AB,BC,AC分别表示a 与b,b与c, a与c的公垂线段.
AC=AB+BC=5+2=7(cm)
因此a与c的距离是7 cm.
【变式练习】设直线a、b、c是三条平行直线。已知a与b的距离为5厘米,b与c的距离为2厘米,则a与c的距离为( ) A、7cm B、3cm
C、7cm或3cm D、以上都不对
【解析】直线c的位置有两种情况:一是如上题图情形,此时a,c的距离是7cm,二是直线c在直线a、b之间,此时a,c之间的距离是3cm.所以选C。
a
b
c
C
a
b
c
课堂练习 1、如图, MN∥AB,P,Q为直线MN 上的任意两点,三角形PAB和三角形QAB的面积有什么关系?为什么?
【解】三角形PAB与三角形QAB的面积相等。
理由:因为MN∥AB,则点P、Q到AB的距离相等,所以三角形PAB与三角形QAB的边AB上的高相等,又边AB公共,所以这两个三角形面积相等。
2、如图的四边形中,∠A=∠B=∠C=∠D=90°,这样的四边形叫做矩形.矩形的两组对边AB和DC,AD和BC相等吗?为什么?
【解】相等,
理由:AD、BC平行,且AB、DC是AD、BC两平行线间的公垂线段,所以AB=DC,同样的道理,AD=BC.
归纳小结:
这节课你有什么收获?
1、什么叫公垂线和公垂线段?
2、两平行线间的距离是指公垂线段的长,是数量,不是图形。
