沪科版数学八年级下册 19.3《等腰梯形》-课件(共17张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 19.3《等腰梯形》-课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 906.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-05 21:31:28 | ||
图片预览

文档简介
(共17张PPT)
沪科版数学八年级下册
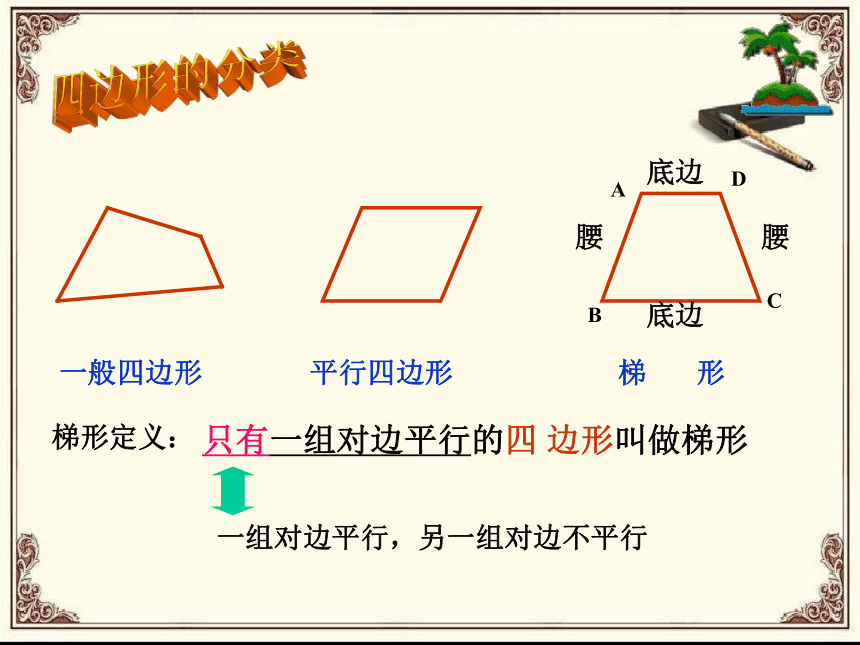
一般四边形
平行四边形
梯 形
梯形定义:
只有一组对边平行的四 边形叫做梯形
一组对边平行,另一组对边不平行
底边
底边
腰
腰
A
B
C
D
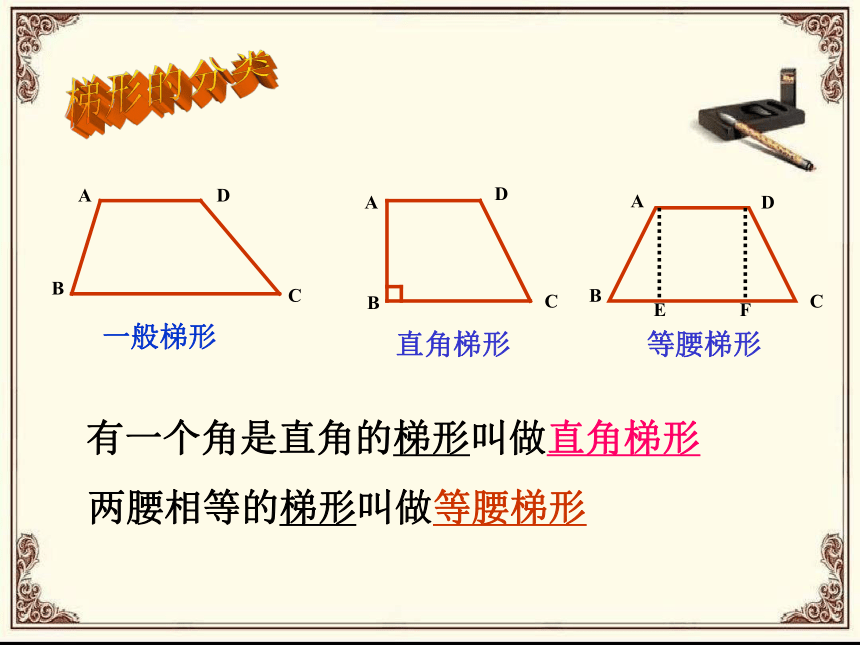
一般梯形
直角梯形
等腰梯形
有一个角是直角的梯形叫做直角梯形
两腰相等的梯形叫做等腰梯形
A
B
C
D
A
B
C
C
D
A
B
D
E
F
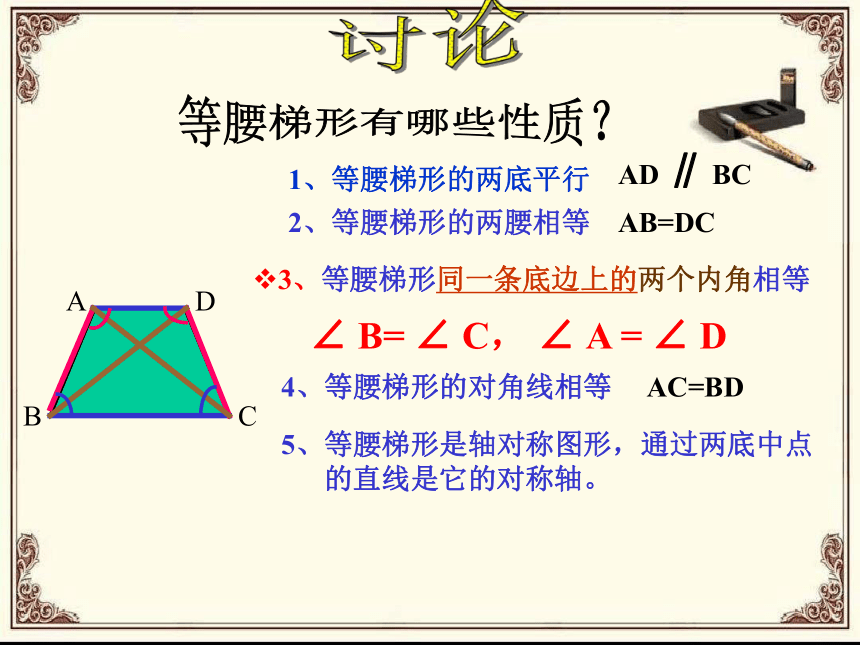
A
B
C
D
1、等腰梯形的两底平行
2、等腰梯形的两腰相等
3、等腰梯形同一条底边上的两个内角相等
AD ∥ BC
AB=DC
4、等腰梯形的对角线相等
AC=BD
5、等腰梯形是轴对称图形,通过两底中点
的直线是它的对称轴。
∠ B= ∠ C, ∠ A = ∠ D
等腰梯形同一条底边上的两个内角相等
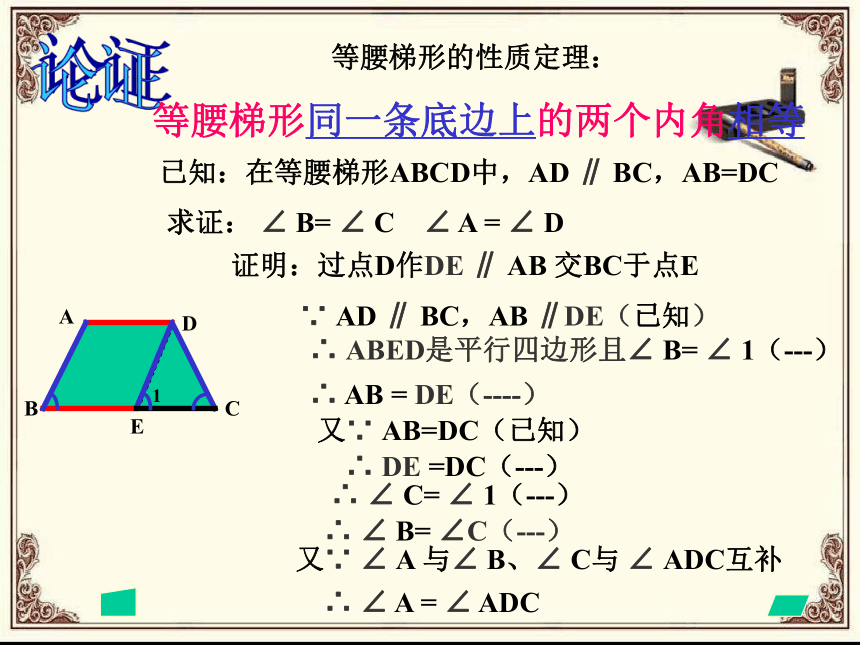
等腰梯形的性质定理:
A
B
C
D
E
1
已知:在等腰梯形ABCD中,AD ∥ BC,AB=DC
求证: ∠ B= ∠ C ∠ A = ∠ D
证明:过点D作DE ∥ AB 交BC于点E
∴ AB = DE(----)
又∵ AB=DC(已知)
∴ DE =DC(---)
∴ ∠ C= ∠ 1(---)
∴ ∠ B= ∠C(---)
又∵ ∠ A 与∠ B、∠ C与 ∠ ADC互补
∴ ∠ A = ∠ ADC
∵ AD ∥ BC,AB ∥DE(已知)
∴ ABED是平行四边形且∠ B= ∠ 1(---)
等腰梯形同一条底边上的两个内角相等
等腰梯形的性质定理:
A
B
C
D
E
1
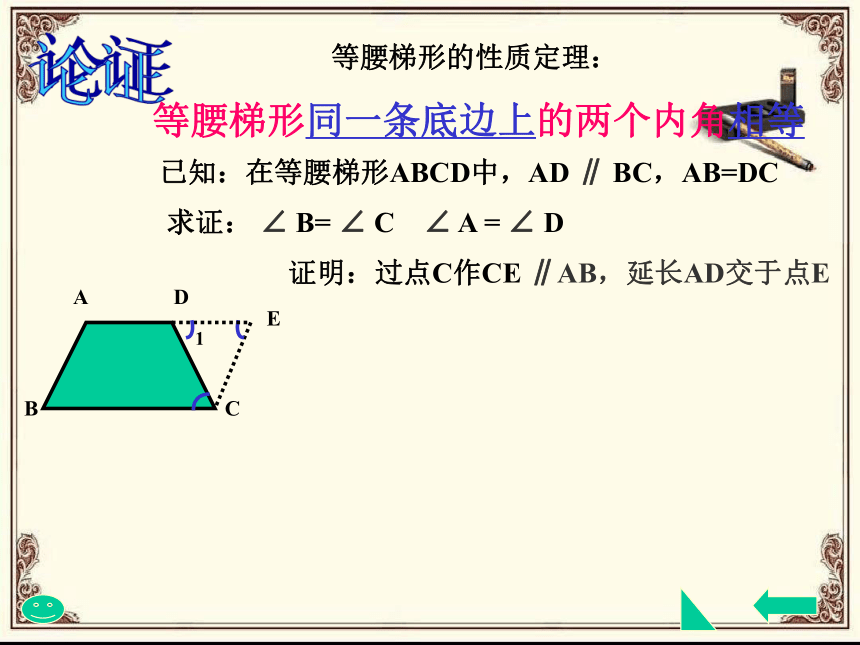
已知:在等腰梯形ABCD中,AD ∥ BC,AB=DC
求证: ∠ B= ∠ C ∠ A = ∠ D
证明:过点C作CE ∥AB,延长AD交于点E
等腰梯形同一底边上的两个内角相等
等腰梯形的性质定理:
A
B
C
D
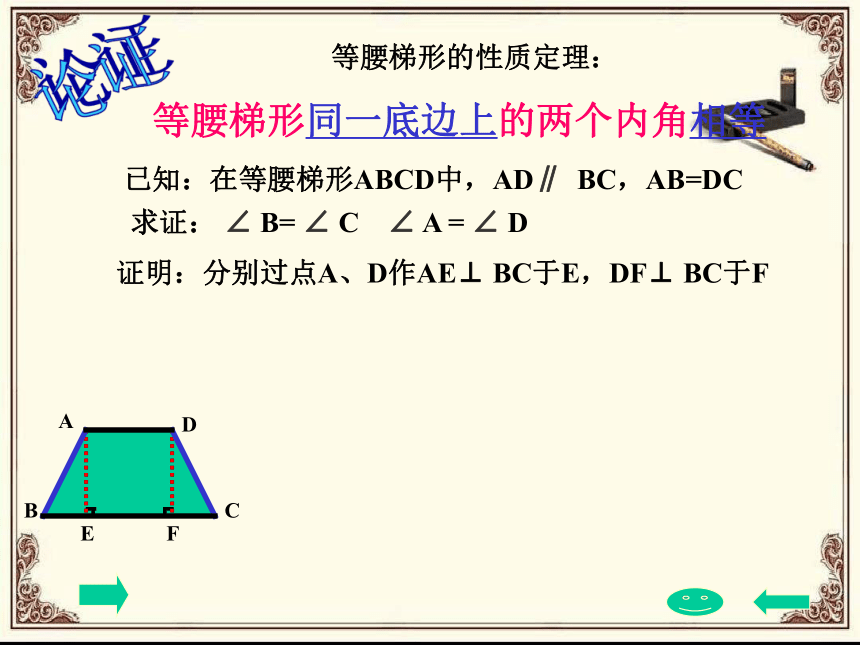
已知:在等腰梯形ABCD中,AD∥ BC,AB=DC
求证: ∠ B= ∠ C ∠ A = ∠ D
E
F
证明:分别过点A、D作AE⊥ BC于E,DF⊥ BC于F
性质定理 等腰梯形的对角线相等
A
B
C
D
已知:在等腰梯形ABCD中,AD ∥ BC,AB=DC
1
2
求证: AC=BD
证明: ∵ ABCD是等腰梯形
∴ ∠ ABC= ∠ DCB
又∵ AB=DC BC=CB
∴ △ ABC≌△DCB(SAS)
∴AC=BD(全等三角形的对应边相等)
O
(OB = OC OA = OD)
(等腰梯形同一条底边上的两个内角相等)
判定定理 同一底上的两个内角相等的梯 形是等腰梯形
已知:在梯形ABCD中,
AD∥BC,∠B= ∠C .
求证:AB=DC.
A
B
C
D
证明:过点D作DE ∥AB交BC于E
E
A
B
C
D
E
四边形ABCD是等腰梯形,延长两腰BA,
CD后交于点E,问△ EBC和△ EAD的形状如何?
证明:∵ABCD是等腰梯形
∴ ∠ B= ∠ C
∴EB = EC
∴ △ EBC是等腰三角形
∵ AD∥ BC
∴ ∠ B= ∠EAD ∠ C = ∠EDA
∴EA = ED(等角对等边)
即 △ EAD是等腰三角形
∴∠EAD = ∠EDA(等量代换)
又∵ ∠ B= ∠ C
(等腰梯形同一条底边上的两个内角相等)
如图:已知在等腰梯形ABCD中, AD ∥ BC,
AB=DC =4,AD =3,BC =7,求∠ B的度数。
A
B
C
D
E
4
3
3
4
4
4
如图:已知在等腰梯形ABCD中, AD ∥ BC,
AB=DC =4,AD =3,BC =7,求∠ B的度数。
A
B
C
D
E
F
4
4
3
3
2
2
作 高
平行移腰
平行移腰
平行移对角线
延长两腰
练习1:
已知:等腰梯形的一个底角为600,它的两底分别是6CM,16CM。求这个等腰梯形的周长。
A
B
C
D
6
16
练习2:
求证:两条对角线相等 的梯形是等腰梯形
课堂小结
1)等腰梯形有关性质定理和判定定理的论证。
2)解决等腰梯形问题的一般辅助线的作法。
谢 谢!
沪科版数学八年级下册
一般四边形
平行四边形
梯 形
梯形定义:
只有一组对边平行的四 边形叫做梯形
一组对边平行,另一组对边不平行
底边
底边
腰
腰
A
B
C
D
一般梯形
直角梯形
等腰梯形
有一个角是直角的梯形叫做直角梯形
两腰相等的梯形叫做等腰梯形
A
B
C
D
A
B
C
C
D
A
B
D
E
F
A
B
C
D
1、等腰梯形的两底平行
2、等腰梯形的两腰相等
3、等腰梯形同一条底边上的两个内角相等
AD ∥ BC
AB=DC
4、等腰梯形的对角线相等
AC=BD
5、等腰梯形是轴对称图形,通过两底中点
的直线是它的对称轴。
∠ B= ∠ C, ∠ A = ∠ D
等腰梯形同一条底边上的两个内角相等
等腰梯形的性质定理:
A
B
C
D
E
1
已知:在等腰梯形ABCD中,AD ∥ BC,AB=DC
求证: ∠ B= ∠ C ∠ A = ∠ D
证明:过点D作DE ∥ AB 交BC于点E
∴ AB = DE(----)
又∵ AB=DC(已知)
∴ DE =DC(---)
∴ ∠ C= ∠ 1(---)
∴ ∠ B= ∠C(---)
又∵ ∠ A 与∠ B、∠ C与 ∠ ADC互补
∴ ∠ A = ∠ ADC
∵ AD ∥ BC,AB ∥DE(已知)
∴ ABED是平行四边形且∠ B= ∠ 1(---)
等腰梯形同一条底边上的两个内角相等
等腰梯形的性质定理:
A
B
C
D
E
1
已知:在等腰梯形ABCD中,AD ∥ BC,AB=DC
求证: ∠ B= ∠ C ∠ A = ∠ D
证明:过点C作CE ∥AB,延长AD交于点E
等腰梯形同一底边上的两个内角相等
等腰梯形的性质定理:
A
B
C
D
已知:在等腰梯形ABCD中,AD∥ BC,AB=DC
求证: ∠ B= ∠ C ∠ A = ∠ D
E
F
证明:分别过点A、D作AE⊥ BC于E,DF⊥ BC于F
性质定理 等腰梯形的对角线相等
A
B
C
D
已知:在等腰梯形ABCD中,AD ∥ BC,AB=DC
1
2
求证: AC=BD
证明: ∵ ABCD是等腰梯形
∴ ∠ ABC= ∠ DCB
又∵ AB=DC BC=CB
∴ △ ABC≌△DCB(SAS)
∴AC=BD(全等三角形的对应边相等)
O
(OB = OC OA = OD)
(等腰梯形同一条底边上的两个内角相等)
判定定理 同一底上的两个内角相等的梯 形是等腰梯形
已知:在梯形ABCD中,
AD∥BC,∠B= ∠C .
求证:AB=DC.
A
B
C
D
证明:过点D作DE ∥AB交BC于E
E
A
B
C
D
E
四边形ABCD是等腰梯形,延长两腰BA,
CD后交于点E,问△ EBC和△ EAD的形状如何?
证明:∵ABCD是等腰梯形
∴ ∠ B= ∠ C
∴EB = EC
∴ △ EBC是等腰三角形
∵ AD∥ BC
∴ ∠ B= ∠EAD ∠ C = ∠EDA
∴EA = ED(等角对等边)
即 △ EAD是等腰三角形
∴∠EAD = ∠EDA(等量代换)
又∵ ∠ B= ∠ C
(等腰梯形同一条底边上的两个内角相等)
如图:已知在等腰梯形ABCD中, AD ∥ BC,
AB=DC =4,AD =3,BC =7,求∠ B的度数。
A
B
C
D
E
4
3
3
4
4
4
如图:已知在等腰梯形ABCD中, AD ∥ BC,
AB=DC =4,AD =3,BC =7,求∠ B的度数。
A
B
C
D
E
F
4
4
3
3
2
2
作 高
平行移腰
平行移腰
平行移对角线
延长两腰
练习1:
已知:等腰梯形的一个底角为600,它的两底分别是6CM,16CM。求这个等腰梯形的周长。
A
B
C
D
6
16
练习2:
求证:两条对角线相等 的梯形是等腰梯形
课堂小结
1)等腰梯形有关性质定理和判定定理的论证。
2)解决等腰梯形问题的一般辅助线的作法。
谢 谢!
