18.1 勾股定理 课件
图片预览



文档简介
课件19张PPT。第十八章 勾股定理
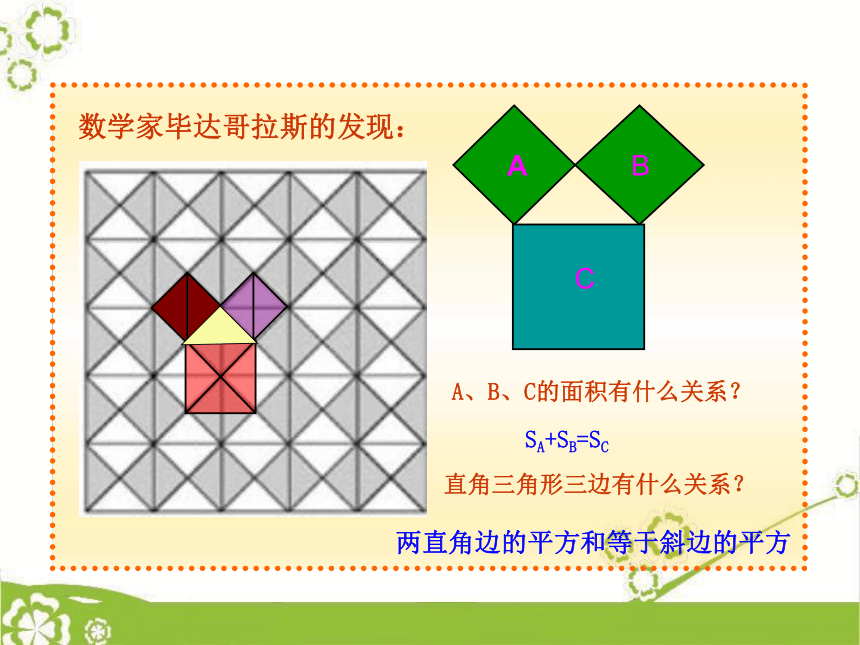
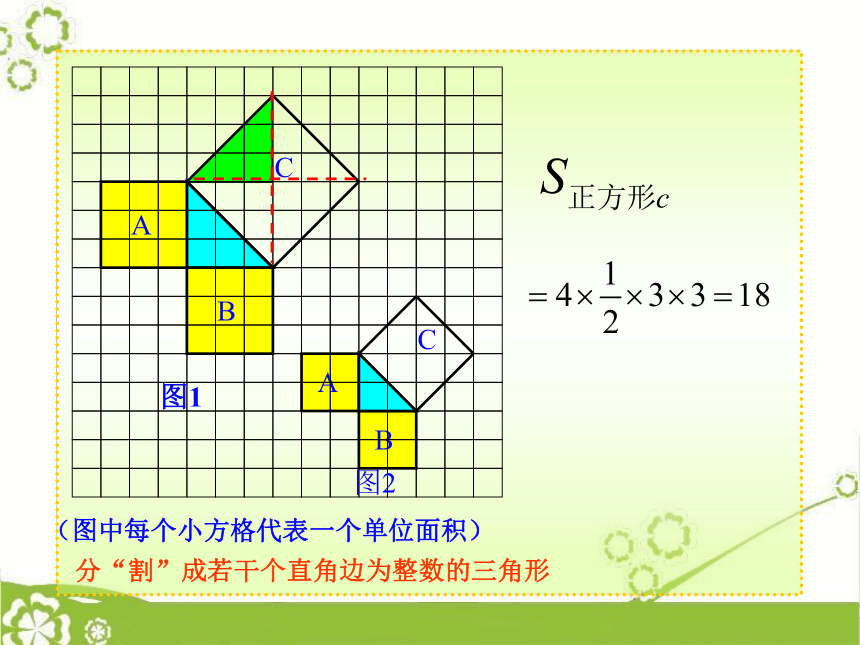
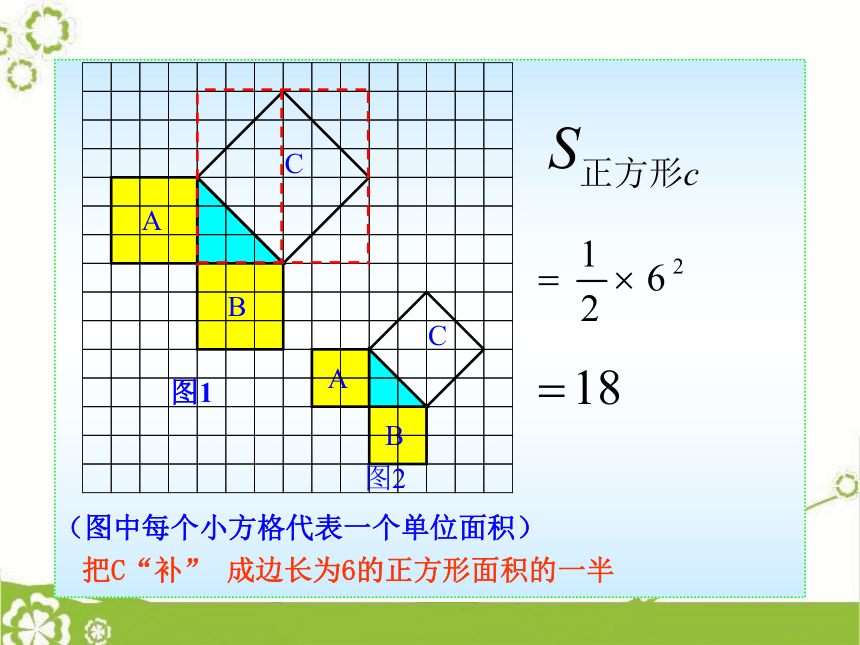
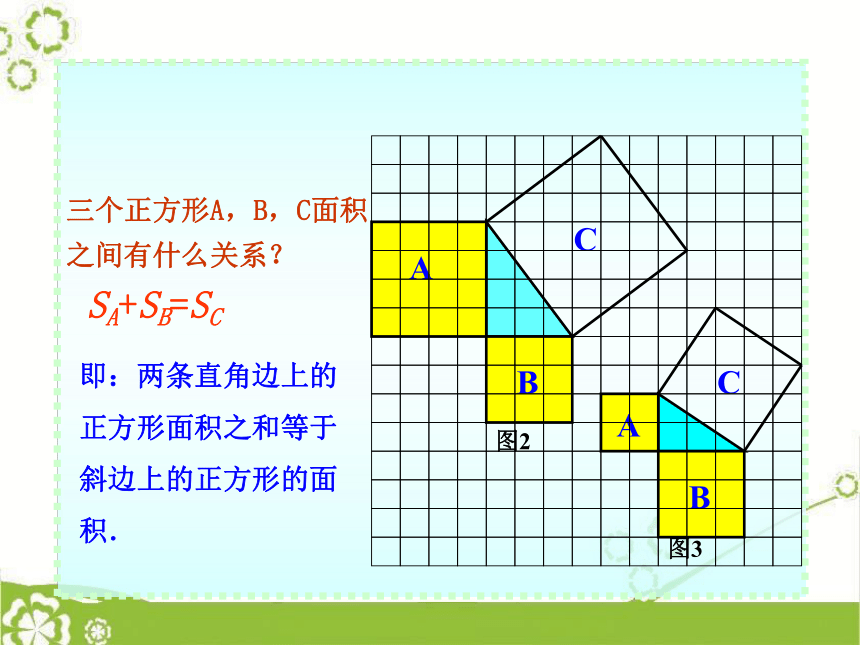
18.1 勾股定理这就是本届大会会徽的图案.你见过这个图案吗?你听说过勾股定理吗? 这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”. 相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系. 我们也来观察右图中的地面,看看有什么发现?数学家毕达哥拉斯的发现:A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直角边的平方和等于斜边的平方分“割”成若干个直角边为整数的三角形把C“补” 成边长为6的正方形面积的一半三个正方形A,B,C面积之间有什么关系?SA+SB=SC即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.acbSA+SB=SC设:直角三角形的三边长分别是a、b、c,猜想:两直角边a、b与斜边c 之间的关系?a2+b2=c2┏a2+b2=c2acb如果直角三角形的两直角边长分别是a、b,斜边长是c,那么a2+b2=c2。勾股弦命题1:赵爽弦图的证法化简得: c2 =a2+ b2. baa经过证明被确认正确的命题叫做定理.┏a2+b2=c2acb直角三角形两直角边的平方和等于斜边的平方.勾股弦勾股定理(毕达哥拉斯定理) 1.求下列图中表示边的未知数x、y、z的值.①81144xyz②③2.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x3.在Rt△ABC中, a=5,c=13,则下列计算正确的是
( )B正确运用6.在一个直角三角形中, 两边长分别为3、4,则第三边的长为________5 或 4.在等腰Rt△ABC中, a=b=1,则c=___5.在Rt△ABC中, ∠A=30°,AB=2,则BC= __AC=___第4题图第5题图1巩固提高 DA7.蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE智能提升 34125688.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49Thank you!
18.1 勾股定理这就是本届大会会徽的图案.你见过这个图案吗?你听说过勾股定理吗? 这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”. 相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系. 我们也来观察右图中的地面,看看有什么发现?数学家毕达哥拉斯的发现:A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直角边的平方和等于斜边的平方分“割”成若干个直角边为整数的三角形把C“补” 成边长为6的正方形面积的一半三个正方形A,B,C面积之间有什么关系?SA+SB=SC即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.acbSA+SB=SC设:直角三角形的三边长分别是a、b、c,猜想:两直角边a、b与斜边c 之间的关系?a2+b2=c2┏a2+b2=c2acb如果直角三角形的两直角边长分别是a、b,斜边长是c,那么a2+b2=c2。勾股弦命题1:赵爽弦图的证法化简得: c2 =a2+ b2. baa经过证明被确认正确的命题叫做定理.┏a2+b2=c2acb直角三角形两直角边的平方和等于斜边的平方.勾股弦勾股定理(毕达哥拉斯定理) 1.求下列图中表示边的未知数x、y、z的值.①81144xyz②③2.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x3.在Rt△ABC中, a=5,c=13,则下列计算正确的是
( )B正确运用6.在一个直角三角形中, 两边长分别为3、4,则第三边的长为________5 或 4.在等腰Rt△ABC中, a=b=1,则c=___5.在Rt△ABC中, ∠A=30°,AB=2,则BC= __AC=___第4题图第5题图1巩固提高 DA7.蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE智能提升 34125688.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49Thank you!
