18.2 勾股定理的逆定理 课件
文档属性
| 名称 | 18.2 勾股定理的逆定理 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-08 13:06:53 | ||
图片预览






文档简介
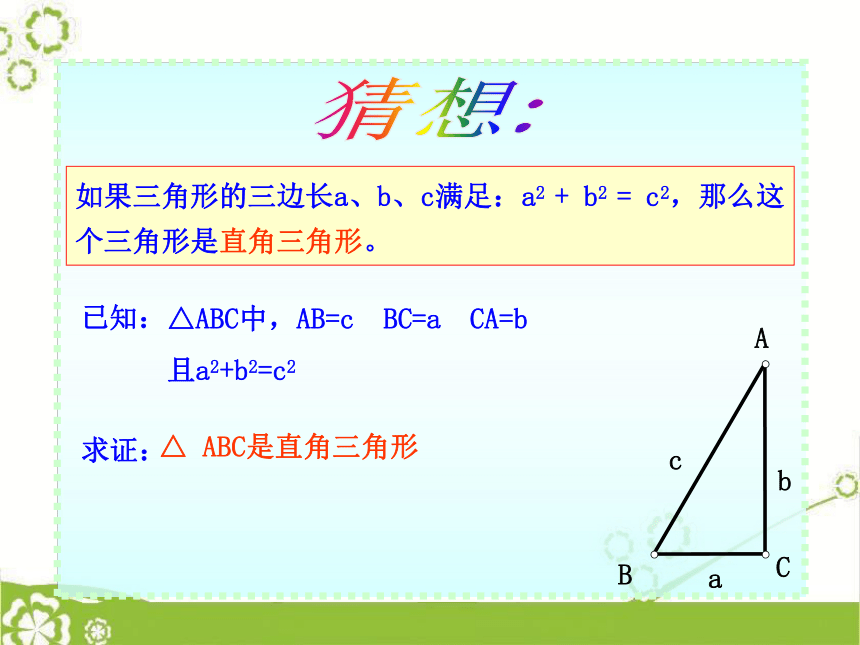
课件17张PPT。勾股定理的逆定理 如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2 古埃及人把一根绳子打上等距离的13个结,然后把第1个结和第13个结用木桩钉在一起,再分别用木桩把第4个结和第8个结钉牢(拉直绳子)。三角形的三边有什么关系呢?探索新知你能猜想出其中的数学道理吗?猜想:如果三角形的三边长a、b、c满足:a2 + b2 = c2,那么这个三角形是直角三角形。已知:△ABC中,AB=c BC=a CA=b
且a2+b2=c2求证:△ ABC是直角三角形已知:在△ABC中,AB=c,BC=a,CA=b,并且 ABbcab 证明:作?
在△ABC和△ ∴?ABC ∠C=∠ Ca(如图)求证:∠C=90°使∠则有中,△=90°≌=90°,题设和结论正好相反的两个命题,叫做互逆命题其中一个叫做原命题,另一个叫做原命题的逆命题 勾股定理的逆命题勾股定理互逆命题(逆定理)(互逆定理)如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2 巩固提高请指出下列命题的逆命题,(1)两直线平行,同位角相等。
(2)对顶角相等。
(3)如果两个实数相等,那么它们的绝对值相等。
(4)全等三角形的对应边相等。例1 判断由线段a、b、c组成的三角形是不是直角三角形:
(1)a=15, b=8, c=17
(2)a=13, b=14,c=15解:(1)像8,15,17这样,能够成为直角三角形三条边长的三个正整数,称为勾股数(或勾股弦数). 1、判断下列△ABC是不是直角三角形?(3) a=15 b=20 c=25 (2) a=13 b=14 c=15 (4) a:b: c=3:4:5 分析:根据题意我们可画出示意图如图所示,则可以看到应用新知2、工厂生产的产品都有一定的规格要求,如图所示:该模板中的AB、BC 相交成直角才符合规定。你能测出这个零件是否合格呢?(身边只有刻度尺)3、观察下列表格:挑战自我84854、如果△ABC的三边分别为a、b、c且满足a2+b2+c2
+50=6a+8b+10c,判定△ABC的形状. 这个三角形是直角三角形. 谈谈这节课你的收获吧!
且a2+b2=c2求证:△ ABC是直角三角形已知:在△ABC中,AB=c,BC=a,CA=b,并且 ABbcab 证明:作?
在△ABC和△ ∴?ABC ∠C=∠ Ca(如图)求证:∠C=90°使∠则有中,△=90°≌=90°,题设和结论正好相反的两个命题,叫做互逆命题其中一个叫做原命题,另一个叫做原命题的逆命题 勾股定理的逆命题勾股定理互逆命题(逆定理)(互逆定理)如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2 巩固提高请指出下列命题的逆命题,(1)两直线平行,同位角相等。
(2)对顶角相等。
(3)如果两个实数相等,那么它们的绝对值相等。
(4)全等三角形的对应边相等。例1 判断由线段a、b、c组成的三角形是不是直角三角形:
(1)a=15, b=8, c=17
(2)a=13, b=14,c=15解:(1)像8,15,17这样,能够成为直角三角形三条边长的三个正整数,称为勾股数(或勾股弦数). 1、判断下列△ABC是不是直角三角形?(3) a=15 b=20 c=25 (2) a=13 b=14 c=15 (4) a:b: c=3:4:5 分析:根据题意我们可画出示意图如图所示,则可以看到应用新知2、工厂生产的产品都有一定的规格要求,如图所示:该模板中的AB、BC 相交成直角才符合规定。你能测出这个零件是否合格呢?(身边只有刻度尺)3、观察下列表格:挑战自我84854、如果△ABC的三边分别为a、b、c且满足a2+b2+c2
+50=6a+8b+10c,判定△ABC的形状. 这个三角形是直角三角形. 谈谈这节课你的收获吧!
