探索三角形全等的条件(一)

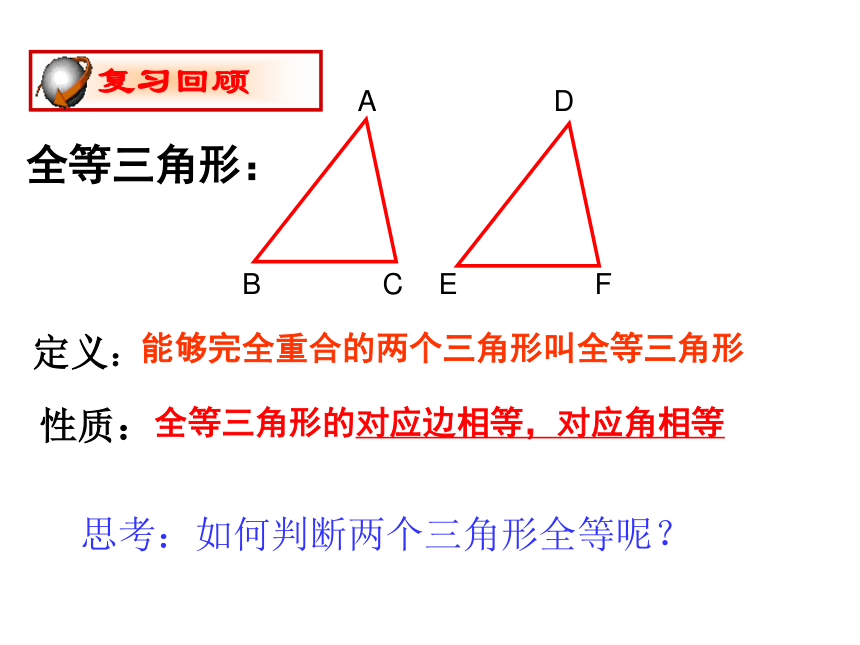
课件19张PPT。探索三角形全等的条件(一)全等三角形的对应边相等，对应角相等全等三角形：能够完全重合的两个三角形叫全等三角形定义：性质： 复习回顾思考：如何判断两个三角形全等呢？学习目标了解三角形全等“边边边”的条件，三角形的稳定性。
经历探索三角形全等条件的过程，体会利用操作、归纳获得数学结论的程；
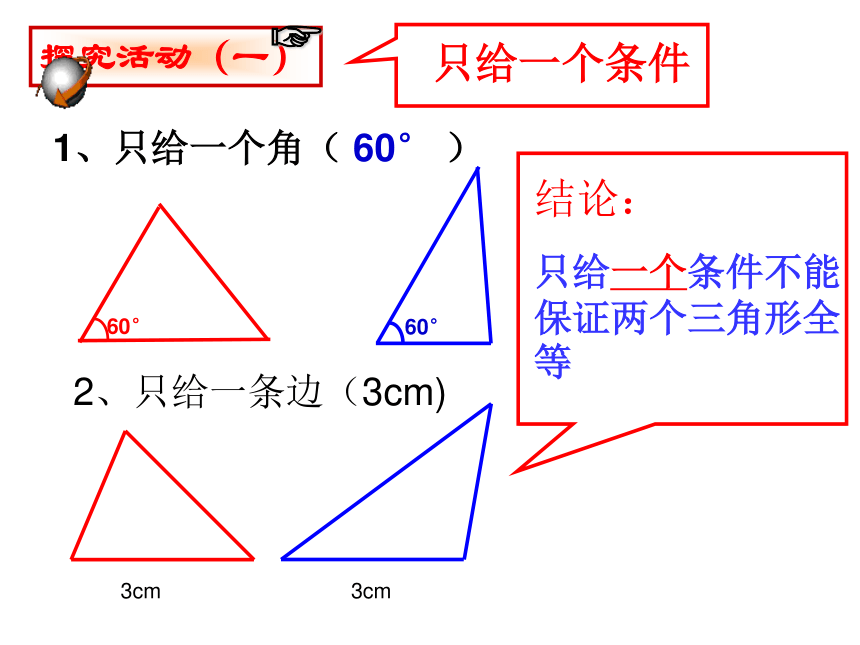
探究活动（一）?1、只给一个角（ 60° ）只给一个条件2、只给一条边（3cm)结论：
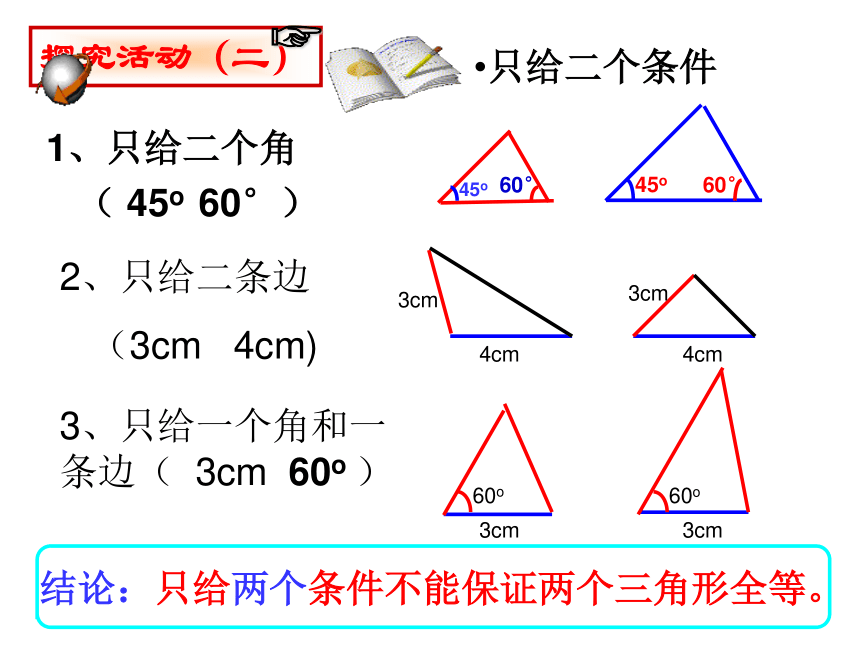
只给一个条件不能保证两个三角形全等1、只给二个角
（ 45o 60°）只给二个条件2、只给二条边
（3cm 4cm)3、只给一个角和一条边（ 3cm 60o ）结论：只给两个条件不能保证两个三角形全等。 有四种可能:(三个角、三条边、二角一边、二边一角)
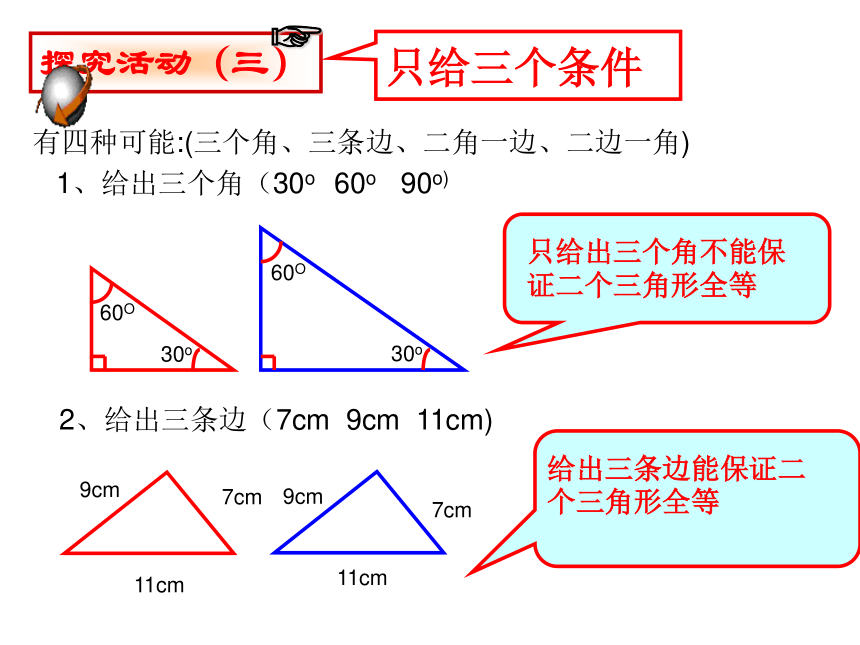
1、给出三个角（30o 60o 90o)
探究活动（三）?2、给出三条边（7cm 9cm 11cm)只给出三个角不能保证二个三角形全等给出三条边能保证二个三角形全等只给三个条件三角形全等条件的探究探究1、一个条件（一条边或一个角)对应相等的二个三角形全等(不成立)
探究2、两个条件（两个角、两条边、一个角一条边）对应相等的两
三角形全等（不成立）
探究3、有三个条件（三个角、三条边、两角一边、两边一角）
三角对应相等的两个三角形全等（不成立）
三边对应相等的两个三角形全等（成立）
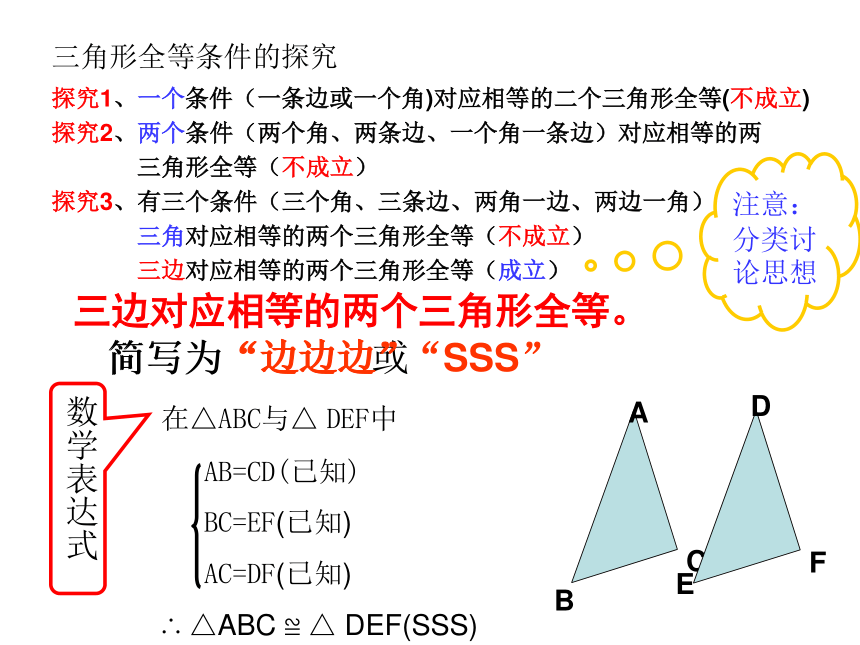
三边对应相等的两个三角形全等。简写为“边边边”或“SSS”数学表达式在△ABC与△ DEF中
AB=CD(已知)
BC=EF(已知)
AC=DF(已知)
∴ △ABC ≌ △ DEF(SSS)注意：
分类讨论思想简写为“边边边”例1、如右图，△ABC是一个钢架，AB=AC，AD是连接A与BC的中点D的支架。 求证:(1)△ ABD≌ △ ACD
(2) ∠B=∠C证明：∵D是BC中点∴BD=CD在△ ABD和△ ACD中AB=AC（已知）BD=CD（已证）AD=AD∴ △ ABD≌ △ ACD(SSS)(公共边）（1）（2）由（1）知△ABD≌△ACD∴ ∠B=∠C（全等三角形对应角相等）要证明两个三角形全等，首先看它们的三边是否对应相等。
例1、如右图，△ABC是一个钢架，AB=AC，AD是连接A与BC的中点D的支架。 求证:(1)△ ABD≌ △ ACD
(2) ∠B=∠C证明：∵D是BC中点∴BD=CD在△ ABD和△ ACD中AB=AC（已知）BD=CD（已证）AD=AD∴ △ ABD≌ △ ACD(SSS)(公共边）（1）（2）由（1）知△ABD≌△ACD∴ ∠B=∠C（全等三角形对应角相等）三角形全等书写一般步骤：1、写出在哪两个三角形中2、摆出的三个条件用大括号括起来3、写出全等结论注意：对应的点，应该
写在对应的位置 理由：由上面的结论可知，只要三角形三边长度确定了，这个三角形的形状和大小就完全确定了，三角形的这个性质叫做三角形稳定性。三角形具有稳定性四边形不具有稳定性三角形的稳定性探究活动（四）?你知道这是为什么吗？ 当堂达标1、试一试：四边形、五边形不具有稳定性，你能想出什么方法让它们的形状不发生改变吗？ 2、如图，AB=AD，BC=DC，试证明△ABC和△ADC全等。ABC证明：在△ABC和△ADC中
AB=AD（已知）
BC=CD（已知）
__= __（ ）
∴ △ABC △ADC（ ） ACAC公共边≌SSS如图，在四边形ABCD中，AB=CD,AD=BC,试说明，解：在△ ABD和△ CDB中
AB=CD(已知）AD=BC（已知）BD=DB（公共边）∴ △ ABD≌ △ CDB (SSS）注意：对应的点，应该
写在对应的位置3、 如图，已知AC=FE，BC=DE，点A，D，B， F在一条直线上 AD=FB,你觉得△ ABC和△ FDE全等吗？如果全等，请说明理由。解： △ ABC≌△ FDE ，理由是：
∵ AD=FB
∴ AD+DB=FB+DB
即 AB=FD
在△ ABC和△ FDE中
AC=FE（已知）
BC=DE（已知）
AB=FD（已证）
∴ △ ABC≌ △ FDE (SSS）请同学们谈谈本节课的收获与体会本节课你学到了什么？
有什么收获？