勾股定理逆定理
图片预览







文档简介
课件22张PPT。18.2 勾股定理的逆定理八年级数学组学习目标 1、 理解、识记并会正确运用勾股定理的逆定理。
2、 理解什么是互逆命题、逆定理。自学指导 认真看课本P68练习下面至P69练习上面。注意:
① “黄色标签”和“思考云图”中的提示,思考“探究”中的问题。
② 结合实例,理解什么是互逆命题、逆定理。
③ 例1例2的解题思路、步骤和格式。
6分钟后,比谁会用同样的方法正确地做出检测题。 古埃及人把一根绳子打上等距离的13个结,然后把第1个结和第13个结用木桩钉在一起,再分别用木桩把第4个结和第8个结钉牢(拉直绳子)。三角形的三边有什么关系呢?你能猜想出其中的数学道理吗?一,导入由以上实践,我们发现: 如果围成的三角形的三边分别是3,4,5,有下列的关系:“ ”,那么围成的三角形是直角三角形.做一做 如果三角形的三边分别是5cm,12cm,13cm,有下列的关系: .
那么画出的三角形是直角三角形吗?
换成三边分别是6cm,8cm,10cm
呢?
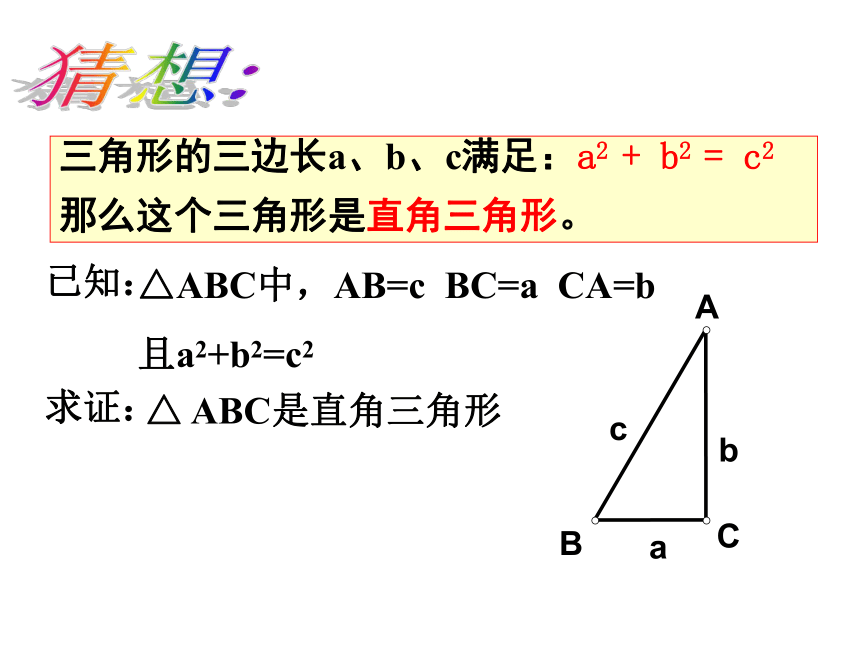
猜想:三角形的三边长a、b、c满足:a2 + b2 = c2
那么这个三角形是直角三角形。已知:△ABC中,AB=c BC=a CA=b
且a2+b2=c2求证:△ ABC是直角三角形
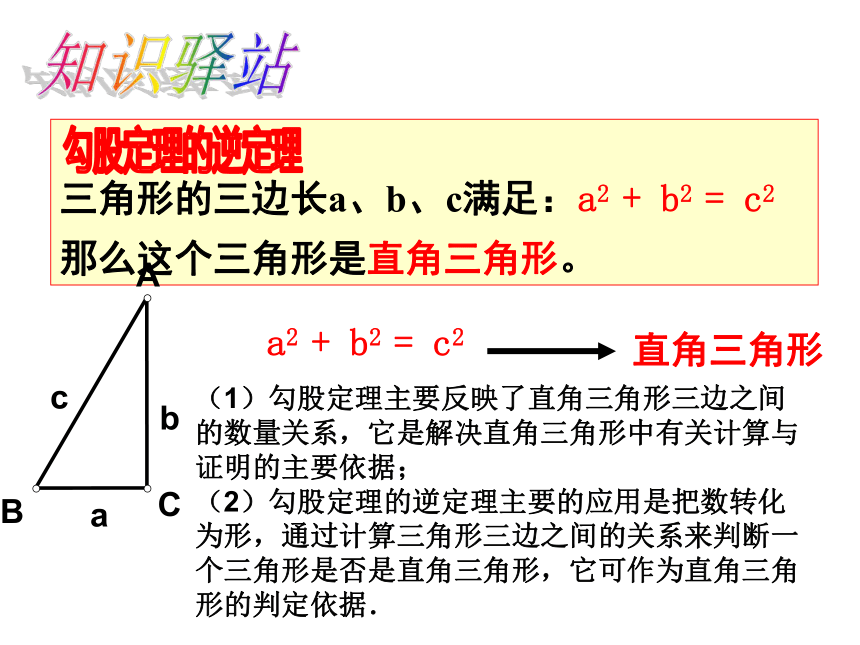
三角形的三边长a、b、c满足:a2 + b2 = c2
那么这个三角形是直角三角形。知识驿站勾股定理的逆定理(1)勾股定理主要反映了直角三角形三边之间的数量关系,它是解决直角三角形中有关计算与证明的主要依据;
(2)勾股定理的逆定理主要的应用是把数转化为形,通过计算三角形三边之间的关系来判断一个三角形是否是直角三角形,它可作为直角三角形的判定依据.1、判断下列△ABC是不是直角三角形?(3) a=15 b=20 c=25 (2) a=13 b=14 c=15 (4) a:b: c=3:4:5 检测一2、观察下列表格:能够成为直角三角形三条边长的
三个正整数,称为勾股数84854、古希腊的哲学家柏拉图曾指出:如果m
表示大于1的整数,a=2m,b=m2-1,c=m2+1,
那么a、b、c为勾股数,你认为对吗?(一)选择题: 检测二 1.在已知下列三组长度的线段中,不能构
成直角三角形的是 ( )
(A)5、12、13 (B)2、3、
(C)4、7、5 (D)1、 、 C (一)选择题: 练 习 2.下列命题中,假命题是 ( )
(A)三个角的度数之比为1 : 3 : 4的三角形是直角三角形
(B)三个角的度数之比为1 : : 2的三角形是直角三角形
(C)三边长度之比为1 : : 2的三角形是直角三角形
(D)三边长度之比为 : : 2的三角形是直角三角形 B 3.如果△ABC的三边分别为a、b、c且满足
a2+b2+c2+50=6a+8b+10c,
判定△ABC的形状. (二)解答题: 练 习 这个三角形是直角三角形. (二)解答题: 1.已知:a=m2-n2,b=2mn,c=m2+n2
(m、n为正整数,m>n).
试判定由a、b、c组成的三角形是不是直
角三角形. 不是练 习 思考1:△ABC三边a,b,c为边向外作正方形,
若S1+S2=S3成立,则△ABC是什么三角形?
为什么?思考2:已知△ABC是直角三角形,以
a,b,c为边向外作正方形,有S1+S2=S3?
为什么?思考交流a2 + b2 = c2直角三角形直角三角形a2 + b2 = c2拓广与应用 例2 “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行, “远航”号每小时航行16海里, “海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗? 例 3.在△ABC中,a=15, b=17, c=8,求此三角形的面积。∴△ABC为直角三角形,且∠B=90°
∴ △ABC的面积为
7.如图:AD⊥CD , AC⊥BC ,AB=13, CD=3 , AD=4 。求:(1)求AC长
(2)求BC长
8.如图, AD⊥CD ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长
(2)∠ACB的度数。变式训练勾股定理与逆定理的综合运用9.如图, AC⊥BC ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长
(2)求 的面积。
课堂小结a2 + b2 = c2直角三角形直角三角形a2 + b2 = c2(1)(2)当堂训练必做题:P76 1、2
选做题:P76 3、5
2、 理解什么是互逆命题、逆定理。自学指导 认真看课本P68练习下面至P69练习上面。注意:
① “黄色标签”和“思考云图”中的提示,思考“探究”中的问题。
② 结合实例,理解什么是互逆命题、逆定理。
③ 例1例2的解题思路、步骤和格式。
6分钟后,比谁会用同样的方法正确地做出检测题。 古埃及人把一根绳子打上等距离的13个结,然后把第1个结和第13个结用木桩钉在一起,再分别用木桩把第4个结和第8个结钉牢(拉直绳子)。三角形的三边有什么关系呢?你能猜想出其中的数学道理吗?一,导入由以上实践,我们发现: 如果围成的三角形的三边分别是3,4,5,有下列的关系:“ ”,那么围成的三角形是直角三角形.做一做 如果三角形的三边分别是5cm,12cm,13cm,有下列的关系: .
那么画出的三角形是直角三角形吗?
换成三边分别是6cm,8cm,10cm
呢?
猜想:三角形的三边长a、b、c满足:a2 + b2 = c2
那么这个三角形是直角三角形。已知:△ABC中,AB=c BC=a CA=b
且a2+b2=c2求证:△ ABC是直角三角形
三角形的三边长a、b、c满足:a2 + b2 = c2
那么这个三角形是直角三角形。知识驿站勾股定理的逆定理(1)勾股定理主要反映了直角三角形三边之间的数量关系,它是解决直角三角形中有关计算与证明的主要依据;
(2)勾股定理的逆定理主要的应用是把数转化为形,通过计算三角形三边之间的关系来判断一个三角形是否是直角三角形,它可作为直角三角形的判定依据.1、判断下列△ABC是不是直角三角形?(3) a=15 b=20 c=25 (2) a=13 b=14 c=15 (4) a:b: c=3:4:5 检测一2、观察下列表格:能够成为直角三角形三条边长的
三个正整数,称为勾股数84854、古希腊的哲学家柏拉图曾指出:如果m
表示大于1的整数,a=2m,b=m2-1,c=m2+1,
那么a、b、c为勾股数,你认为对吗?(一)选择题: 检测二 1.在已知下列三组长度的线段中,不能构
成直角三角形的是 ( )
(A)5、12、13 (B)2、3、
(C)4、7、5 (D)1、 、 C (一)选择题: 练 习 2.下列命题中,假命题是 ( )
(A)三个角的度数之比为1 : 3 : 4的三角形是直角三角形
(B)三个角的度数之比为1 : : 2的三角形是直角三角形
(C)三边长度之比为1 : : 2的三角形是直角三角形
(D)三边长度之比为 : : 2的三角形是直角三角形 B 3.如果△ABC的三边分别为a、b、c且满足
a2+b2+c2+50=6a+8b+10c,
判定△ABC的形状. (二)解答题: 练 习 这个三角形是直角三角形. (二)解答题: 1.已知:a=m2-n2,b=2mn,c=m2+n2
(m、n为正整数,m>n).
试判定由a、b、c组成的三角形是不是直
角三角形. 不是练 习 思考1:△ABC三边a,b,c为边向外作正方形,
若S1+S2=S3成立,则△ABC是什么三角形?
为什么?思考2:已知△ABC是直角三角形,以
a,b,c为边向外作正方形,有S1+S2=S3?
为什么?思考交流a2 + b2 = c2直角三角形直角三角形a2 + b2 = c2拓广与应用 例2 “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行, “远航”号每小时航行16海里, “海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗? 例 3.在△ABC中,a=15, b=17, c=8,求此三角形的面积。∴△ABC为直角三角形,且∠B=90°
∴ △ABC的面积为
7.如图:AD⊥CD , AC⊥BC ,AB=13, CD=3 , AD=4 。求:(1)求AC长
(2)求BC长
8.如图, AD⊥CD ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长
(2)∠ACB的度数。变式训练勾股定理与逆定理的综合运用9.如图, AC⊥BC ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长
(2)求 的面积。
课堂小结a2 + b2 = c2直角三角形直角三角形a2 + b2 = c2(1)(2)当堂训练必做题:P76 1、2
选做题:P76 3、5
