冀教版七年级下册 8.2 完全平方公式课件(共13张PPT)
文档属性
| 名称 | 冀教版七年级下册 8.2 完全平方公式课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 00:00:00 | ||
图片预览



文档简介
(共13张PPT)
冀教版 8.5乘法公式
学习目标
1.通过探索、归纳出完全平方公式,并能运用公式进行相应的计算。
2.了解完全平方公式的几何背景。
a
b
a
b
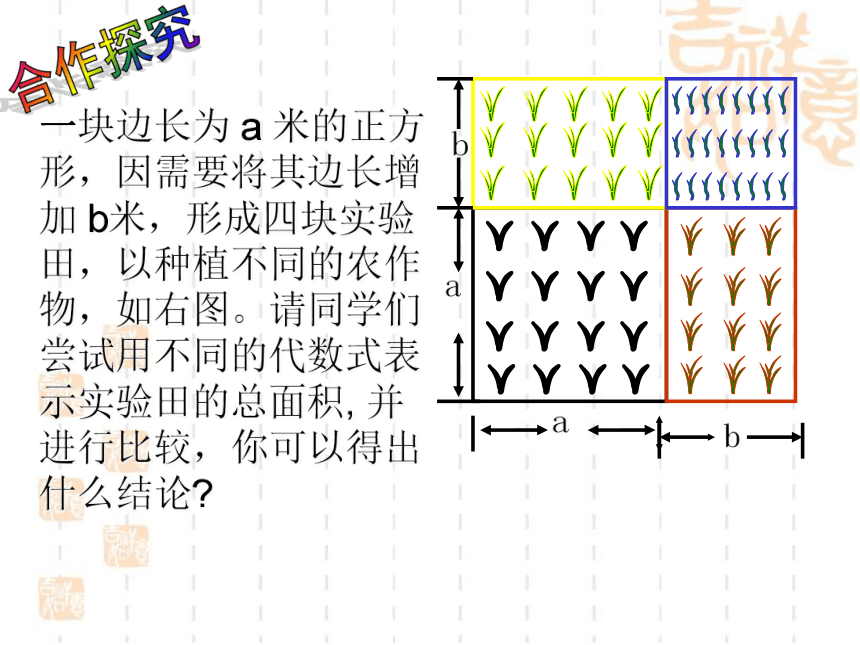
一块边长为 a 米的正方形,因需要将其边长增加 b米,形成四块实验田,以种植不同的农作物,如右图。请同学们尝试用不同的代数式表示实验田的总面积, 并进行比较,你可以得出什么结论
a
b
a
b
2b
3a
3a
2b
请同学们猜想:
(a-b)2
= a2 - 2ab+b2
分析:使用完全平方公式与平方差公式的使用一样, 明确哪个与公式中的 a对应 , 哪个与公式中的 b对应.
(2x+y)
完全平方公式的应用
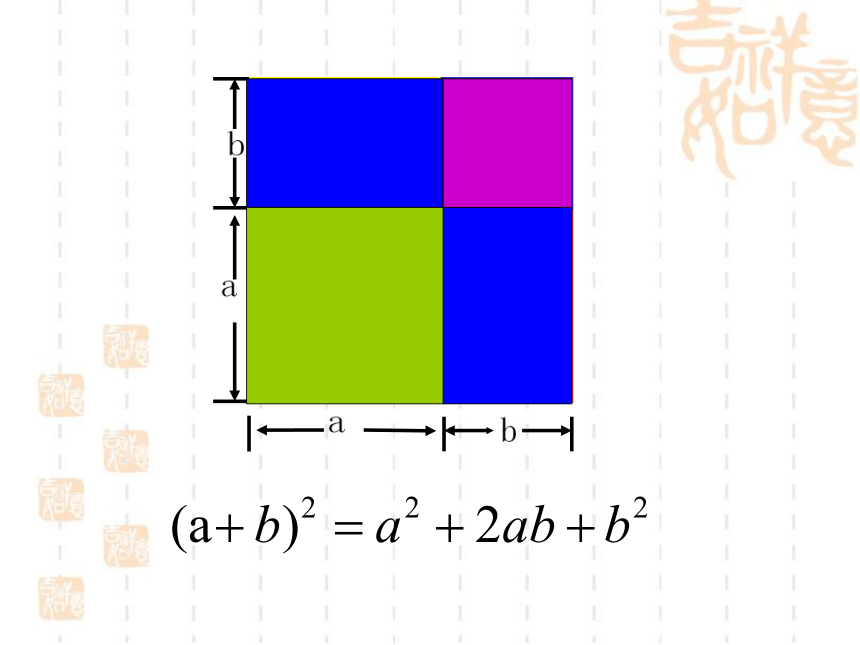
(a + b) =a + 2 a b + b
解
(2X +y﹚
=4x +4xy+y
=(2x)
+ 2 · (2x) · y
+y
快速秒题
竞速比赛:小组内两人为一组,为对方指定下面任意一题,让对方分析题目,并完成解答,需两人全部完成方为完成比赛,用时短的两组同学展示
运用完全平方公式有时能进行
简便方法计算:
解: 1022 =
(100+2)2
请你参考上面的老师的讲解,运用完全平方公式用简便方法计算 992
=1002+2×100×2+22
=10000+400+4
=10404
完全平方公式的变形
a2+b2 =
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
根据完全平方公式,尝试得到下列各式:
(a+b)2-2ab
(a-b)2+2ab
=
冲击新高峰:
已知:
求: 下列代数的值
谢 谢
冀教版 8.5乘法公式
学习目标
1.通过探索、归纳出完全平方公式,并能运用公式进行相应的计算。
2.了解完全平方公式的几何背景。
a
b
a
b
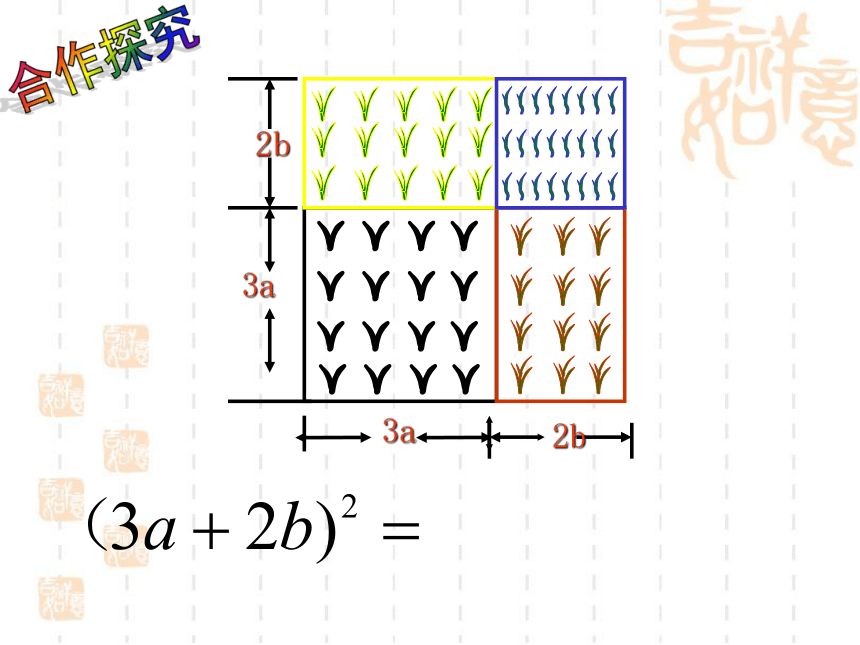
一块边长为 a 米的正方形,因需要将其边长增加 b米,形成四块实验田,以种植不同的农作物,如右图。请同学们尝试用不同的代数式表示实验田的总面积, 并进行比较,你可以得出什么结论
a
b
a
b
2b
3a
3a
2b
请同学们猜想:
(a-b)2
= a2 - 2ab+b2
分析:使用完全平方公式与平方差公式的使用一样, 明确哪个与公式中的 a对应 , 哪个与公式中的 b对应.
(2x+y)
完全平方公式的应用
(a + b) =a + 2 a b + b
解
(2X +y﹚
=4x +4xy+y
=(2x)
+ 2 · (2x) · y
+y
快速秒题
竞速比赛:小组内两人为一组,为对方指定下面任意一题,让对方分析题目,并完成解答,需两人全部完成方为完成比赛,用时短的两组同学展示
运用完全平方公式有时能进行
简便方法计算:
解: 1022 =
(100+2)2
请你参考上面的老师的讲解,运用完全平方公式用简便方法计算 992
=1002+2×100×2+22
=10000+400+4
=10404
完全平方公式的变形
a2+b2 =
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
根据完全平方公式,尝试得到下列各式:
(a+b)2-2ab
(a-b)2+2ab
=
冲击新高峰:
已知:
求: 下列代数的值
谢 谢
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
