鲁教版(五四制)数学六年级下册 7.2 探索直线平行的条件 课件(共19张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学六年级下册 7.2 探索直线平行的条件 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 400.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 08:49:20 | ||
图片预览





文档简介
(共19张PPT)
7.2 探索直线平行的条件(1)
复习引入
在同一平面内两条直线的位置关系有几种?分别是什么?
问题1:
如图,两条直线相交所构成的四个角中分别有何关系?
问题2:
相交和平行
问题3:
复习引入
什么叫两条直线平行?
在同一平面内,不相交的两条直线叫做平行线。
(1)同一平面内
(2) 没有交点
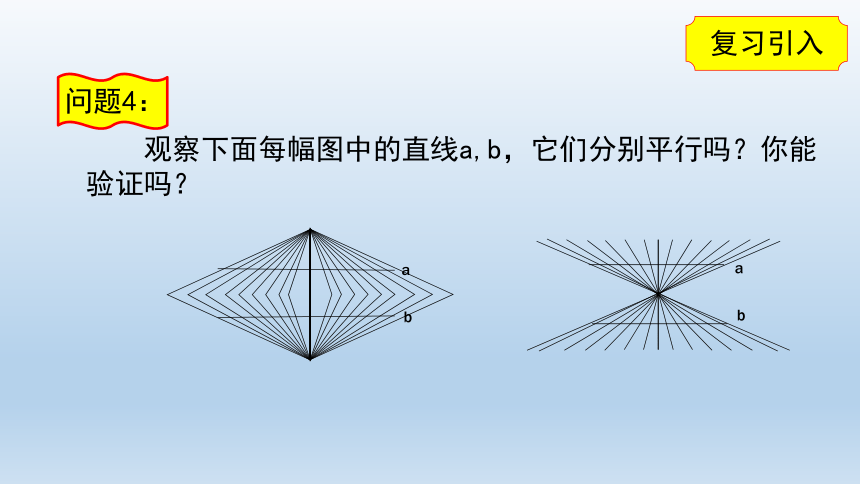
问题4:
观察下面每幅图中的直线a,b,它们分别平行吗?你能验证吗?
复习引入
a
b
a
b
新课学习
1.经历探索直线平行条件的过程,掌握利用同位角相等判别直线平行的结论,并能解决一些问题。
2.会识别由“三线八角”构成的同位角,会用三角尺过已知直线外一点画这条直线的平行线。
3、经历观察、操作、想象、推理、交流等活动,体会利用操作、归纳获得数学结论的过程,进一步发展空间想象、推理能力和有条理表达的能力。
4、在积极参与探索、交流的数学活动中,体验数学与实际生活的密切联系,激发学生的求知欲,感受与他人合作的重要性。
学习目标
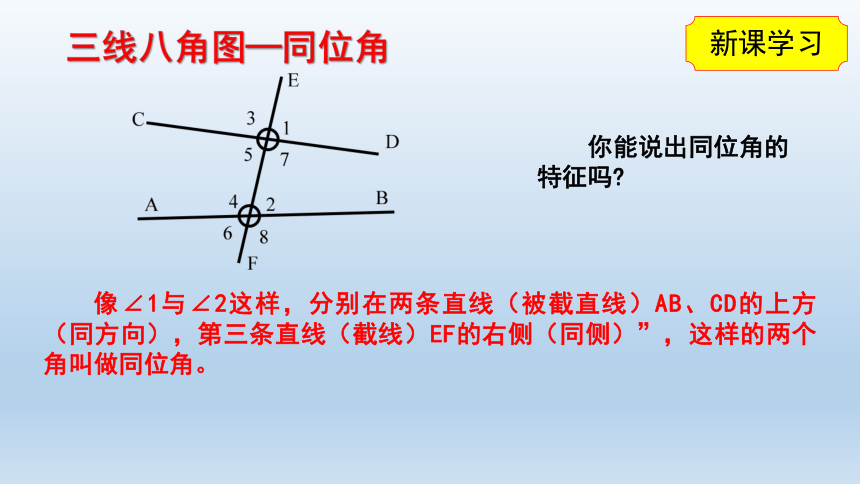
你能说出同位角的特征吗
像∠1与∠2这样,分别在两条直线(被截直线)AB、CD的上方(同方向),第三条直线(截线)EF的右侧(同侧)”,这样的两个角叫做同位角。
新课学习
三线八角图—同位角
新课学习
①
②
③
④
1
2
4
3
5
8
7
6
右上
左上
左下
右下
同位角是 F 形状
如图,∠1和∠2是 ,它是直线_______、_______被直线_______所截而成的,∠2和∠3是 ,它是直线_______、_______被直线_______所截而成的。
AB
BC
DE
同位角
BC
EF
DE
同位角
【巧识同位角】
根据老师的教具演示思考,直线a应满足什么条件才能与直线b平行呢?请你利用教具亲自动手操作。把你的发现在小组内交流。
新课学习
问题:
1
b
a
c
2
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
①直线a和b不平行
②直线a∥b
③直线a和b不平行
新课学习
两条直线平行的条件1
同位角相等,两直线平行。
1
2
符号语言:
∵∠1=∠2
∴a∥b(同位角相等,两直线平行)
新课学习
两条直线被第三条直线所截,如果同位角相等,那么两直线平行
两直线平行,用符号“∥”来表示。
练习1.如图,装修工人正在向墙上钉木条,如果木条b与墙壁的边缘垂直,那么木条a与墙壁的边缘所夹的角为多少度时,才能使木条a与木条b平行?
平行在日常生活中的应用
随堂练习
a
c
b
练习2. 指出下面点阵(点阵中相邻的四个点构成正方形)中互相平行的线段,并说明理由。
练习3. 如图,∠1=∠2=55°, ∠3等于多少度?直线AB、CD平行吗?说明你的理由。
随堂练习
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
A
B
F
E
D
C
G
H
1
2
4
3
问题2:分别过点C、D画直线AB的平行线EF、GH, EF与GH有怎样的位置关系?
议一议
问题1:你还记得怎样用移动三角板的方法画两条平行线吗?你能用这种方法过已知直线AB外一点P画它的平行线吗?请说出其中的道理。
一.放 二.靠 三.推 四.画
通过画图你有什么发现?
要求:过点P时用300的角;过点C时用600的角;过点D时用900的角。
1.过直线外一点有且只有一条直线与这条直线平行。
2.平行于同一条直线的两条直线平行。
注意:与前面学习的画垂线知识的区别。
我的发现
如果b∥a,c∥a,那么b∥c
1.如图,如果∠1=∠2,那么哪两条直线平行?为什么?
2.如图,∠AOC=∠APQ=∠CFE=46°,可得到哪些平行线?为什么?
学以致用
3. 如图,直线EF与∠DBG的两边相交于A,B两点,∠B的同位角是
和 ,∠CAB的同位角是 ,∠ECG的同位角是 。
学以致用
∠DAC
∠ACG
∠BCF
∠EAD
问题1:本节课你认为自己解决的最好的问题是什么?
问题2:本节课你有哪些收获?
总结反思
布置作业
1.(必做题)72页习题7.3第1、2题。
2.(选做题)如图,是由两块相同的直角三角板拼成的,
(1)请写出图中相等的角;
(2)写出图中平行的线段,并说明理由。
A
E
D
C
B
F
7.2 探索直线平行的条件(1)
复习引入
在同一平面内两条直线的位置关系有几种?分别是什么?
问题1:
如图,两条直线相交所构成的四个角中分别有何关系?
问题2:
相交和平行
问题3:
复习引入
什么叫两条直线平行?
在同一平面内,不相交的两条直线叫做平行线。
(1)同一平面内
(2) 没有交点
问题4:
观察下面每幅图中的直线a,b,它们分别平行吗?你能验证吗?
复习引入
a
b
a
b
新课学习
1.经历探索直线平行条件的过程,掌握利用同位角相等判别直线平行的结论,并能解决一些问题。
2.会识别由“三线八角”构成的同位角,会用三角尺过已知直线外一点画这条直线的平行线。
3、经历观察、操作、想象、推理、交流等活动,体会利用操作、归纳获得数学结论的过程,进一步发展空间想象、推理能力和有条理表达的能力。
4、在积极参与探索、交流的数学活动中,体验数学与实际生活的密切联系,激发学生的求知欲,感受与他人合作的重要性。
学习目标
你能说出同位角的特征吗
像∠1与∠2这样,分别在两条直线(被截直线)AB、CD的上方(同方向),第三条直线(截线)EF的右侧(同侧)”,这样的两个角叫做同位角。
新课学习
三线八角图—同位角
新课学习
①
②
③
④
1
2
4
3
5
8
7
6
右上
左上
左下
右下
同位角是 F 形状
如图,∠1和∠2是 ,它是直线_______、_______被直线_______所截而成的,∠2和∠3是 ,它是直线_______、_______被直线_______所截而成的。
AB
BC
DE
同位角
BC
EF
DE
同位角
【巧识同位角】
根据老师的教具演示思考,直线a应满足什么条件才能与直线b平行呢?请你利用教具亲自动手操作。把你的发现在小组内交流。
新课学习
问题:
1
b
a
c
2
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
①直线a和b不平行
②直线a∥b
③直线a和b不平行
新课学习
两条直线平行的条件1
同位角相等,两直线平行。
1
2
符号语言:
∵∠1=∠2
∴a∥b(同位角相等,两直线平行)
新课学习
两条直线被第三条直线所截,如果同位角相等,那么两直线平行
两直线平行,用符号“∥”来表示。
练习1.如图,装修工人正在向墙上钉木条,如果木条b与墙壁的边缘垂直,那么木条a与墙壁的边缘所夹的角为多少度时,才能使木条a与木条b平行?
平行在日常生活中的应用
随堂练习
a
c
b
练习2. 指出下面点阵(点阵中相邻的四个点构成正方形)中互相平行的线段,并说明理由。
练习3. 如图,∠1=∠2=55°, ∠3等于多少度?直线AB、CD平行吗?说明你的理由。
随堂练习
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
A
B
F
E
D
C
G
H
1
2
4
3
问题2:分别过点C、D画直线AB的平行线EF、GH, EF与GH有怎样的位置关系?
议一议
问题1:你还记得怎样用移动三角板的方法画两条平行线吗?你能用这种方法过已知直线AB外一点P画它的平行线吗?请说出其中的道理。
一.放 二.靠 三.推 四.画
通过画图你有什么发现?
要求:过点P时用300的角;过点C时用600的角;过点D时用900的角。
1.过直线外一点有且只有一条直线与这条直线平行。
2.平行于同一条直线的两条直线平行。
注意:与前面学习的画垂线知识的区别。
我的发现
如果b∥a,c∥a,那么b∥c
1.如图,如果∠1=∠2,那么哪两条直线平行?为什么?
2.如图,∠AOC=∠APQ=∠CFE=46°,可得到哪些平行线?为什么?
学以致用
3. 如图,直线EF与∠DBG的两边相交于A,B两点,∠B的同位角是
和 ,∠CAB的同位角是 ,∠ECG的同位角是 。
学以致用
∠DAC
∠ACG
∠BCF
∠EAD
问题1:本节课你认为自己解决的最好的问题是什么?
问题2:本节课你有哪些收获?
总结反思
布置作业
1.(必做题)72页习题7.3第1、2题。
2.(选做题)如图,是由两块相同的直角三角板拼成的,
(1)请写出图中相等的角;
(2)写出图中平行的线段,并说明理由。
A
E
D
C
B
F
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
