沪科版数学八年级下册 19.2平行四边形 课件(共32张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 19.2平行四边形 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 278.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 08:48:28 | ||
图片预览




文档简介
(共32张PPT)
平行四边形
两组对边分别平行的四边形叫做平行四边形。
学一学
A
B
C
D
∵ AD∥BC, AB∥CD
∴四边形ABCD是平行四边形。
几何语言:
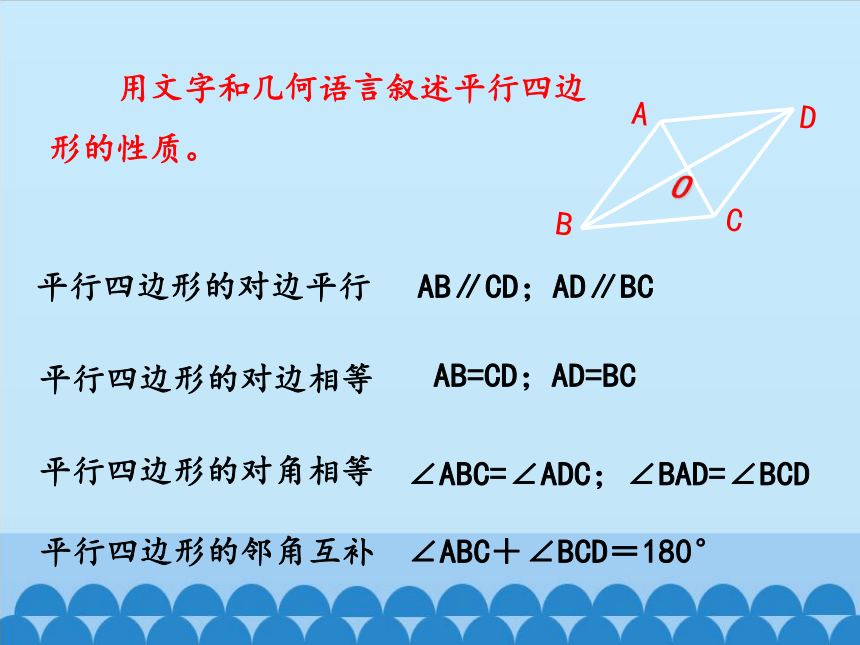
用文字和几何语言叙述平行四边形的性质。
平行四边形的对边相等
平行四边形的对边平行
平行四边形的对角相等
平行四边形的邻角互补
A
B
D
C
O
AB=CD;AD=BC
AB∥CD;AD∥BC
∠ABC=∠ADC;∠BAD=∠BCD
∠ABC+∠BCD=180°
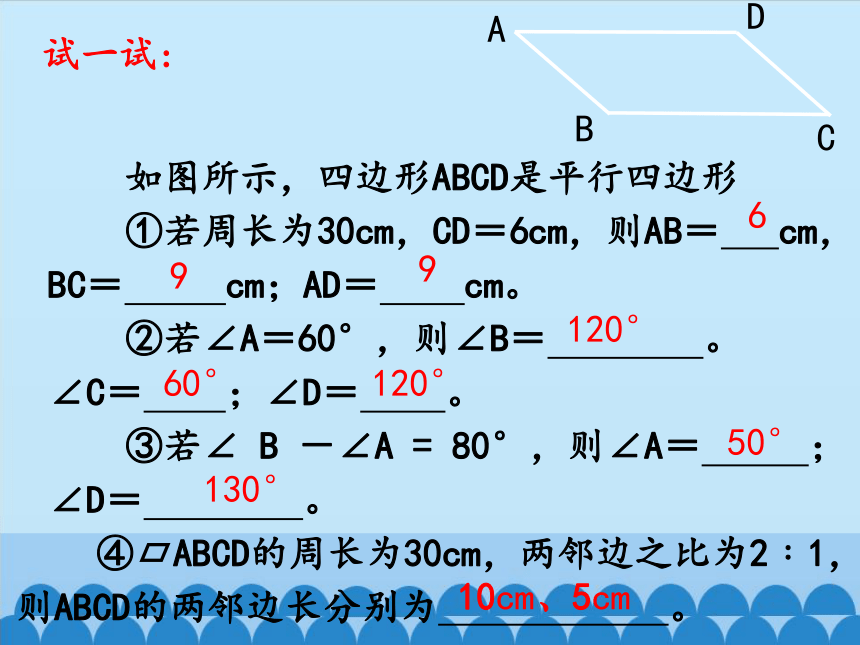
如图所示,四边形ABCD是平行四边形
①若周长为30cm,CD=6cm,则AB= cm,BC= cm;AD= cm。
②若∠A=60°,则∠B= 。
∠C= ;∠D= 。
③若∠ B -∠A = 80°,则∠A= ; ∠D= 。
④ ABCD的周长为30cm,两邻边之比为2﹕1,
则ABCD的两邻边长分别为 。
6
9
9
试一试:
C
D
A
B
120°
120°
60°
50°
130°
10cm、5cm
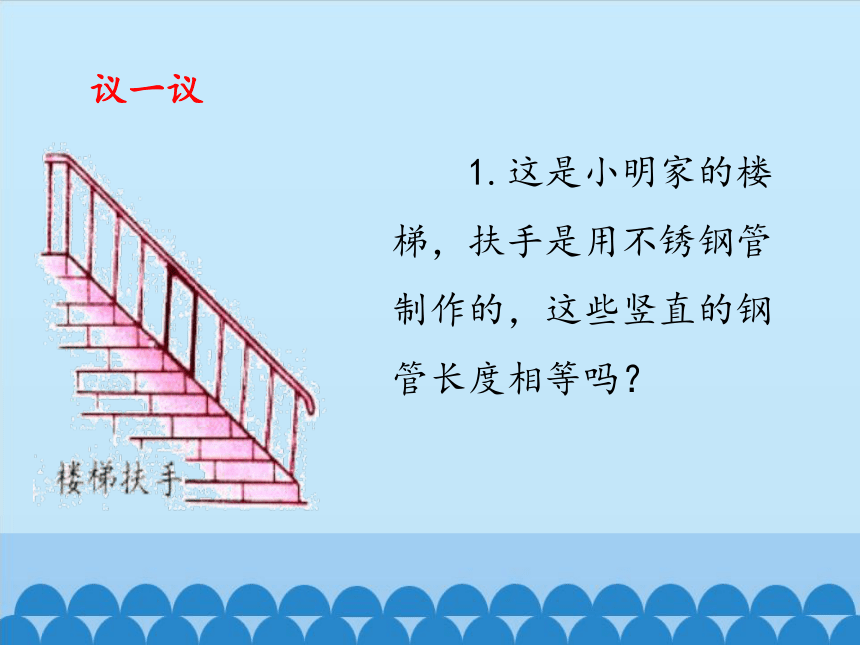
1.这是小明家的楼梯,扶手是用不锈钢管制作的,这些竖直的钢管长度相等吗?
议一议
2.在笔直的铁轨上,夹在两根铁轨之间的枕木是否一样长?
议一议
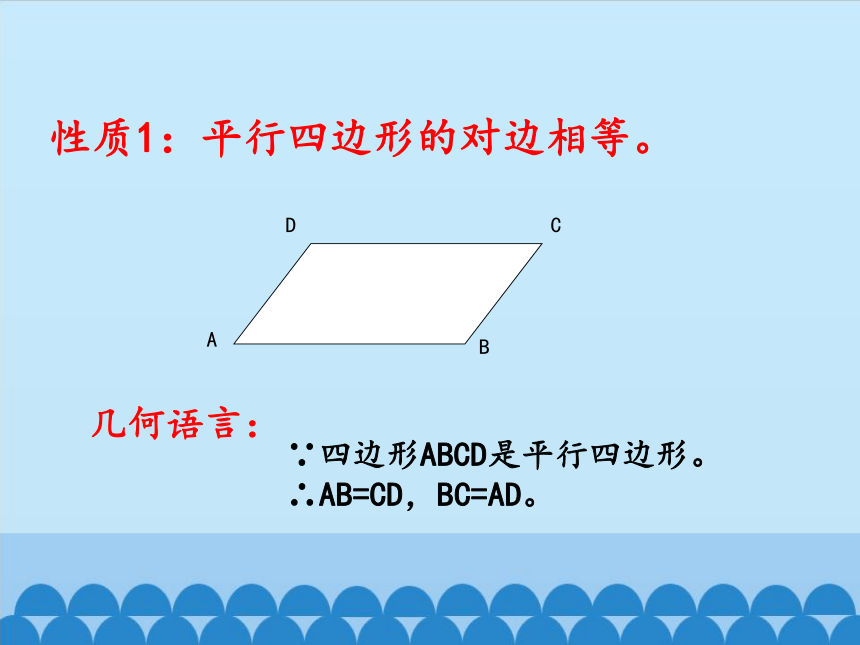
性质1:平行四边形的对边相等。
A
B
C
D
∵四边形ABCD是平行四边形。∴AB=CD,BC=AD。
几何语言:
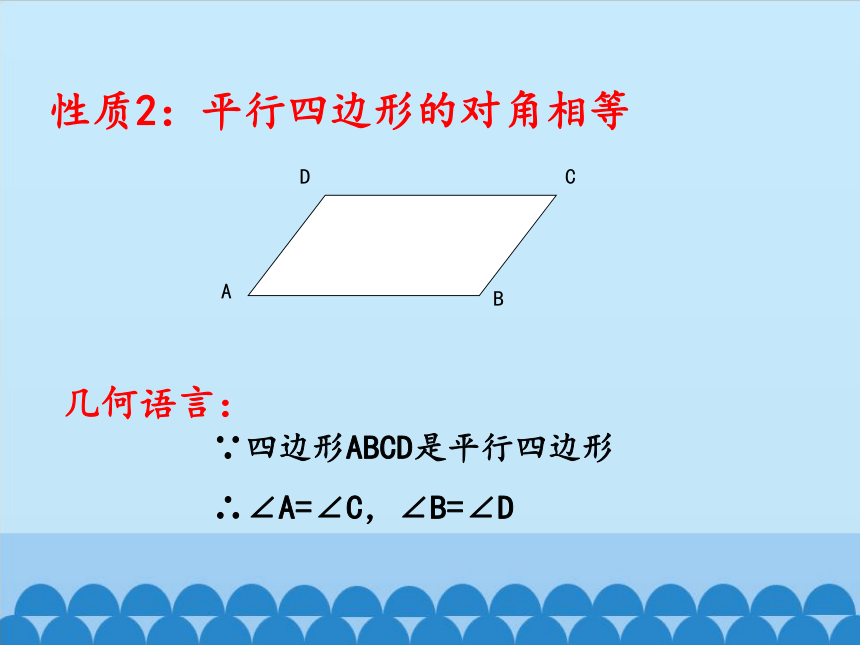
性质2:平行四边形的对角相等
A
B
C
D
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
几何语言:
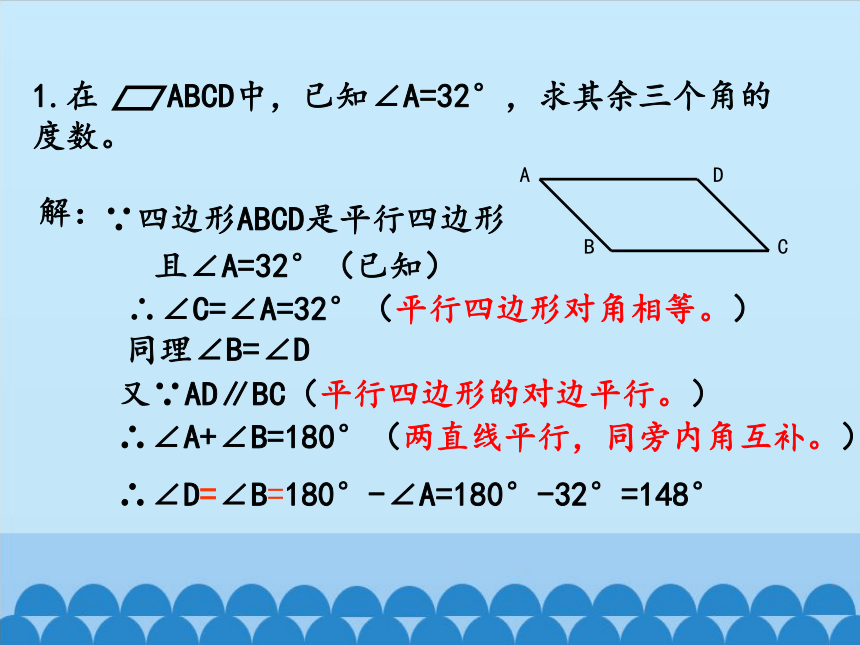
1.在 ABCD中,已知∠A=32°,求其余三个角的度数。
A
B
C
D
∵四边形ABCD是平行四边形
解:
且∠A=32°(已知)
∴∠C=∠A=32°(平行四边形对角相等。) 同理∠B=∠D
又∵AD∥BC(平行四边形的对边平行。)
∴∠A+∠B=180°(两直线平行,同旁内角互补。)
∴∠D=∠B=180°-∠A=180°-32°=148°
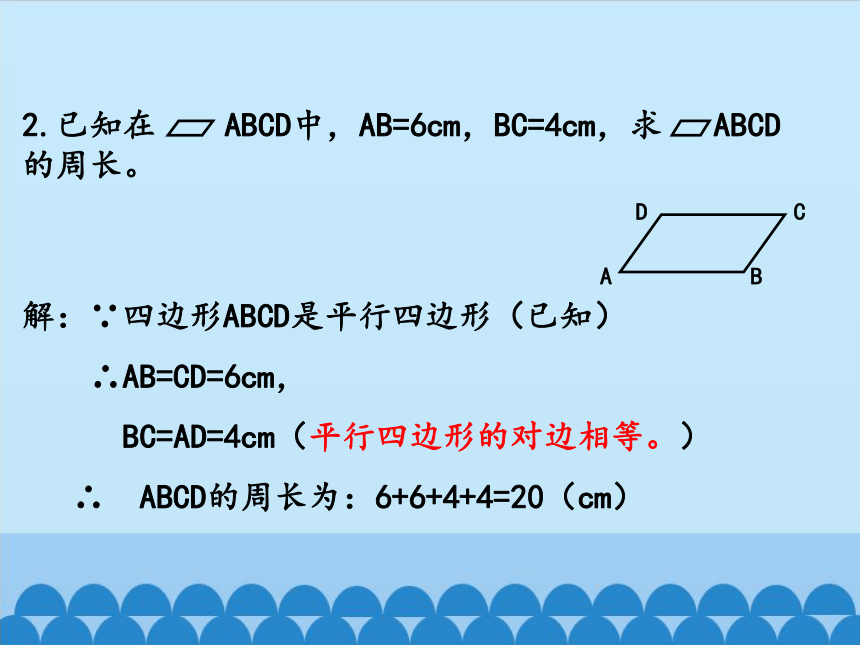
2.已知在 ABCD中,AB=6cm,BC=4cm,求 ABCD 的周长。
A
B
C
D
解:∵四边形ABCD是平行四边形(已知)
∴AB=CD=6cm,
BC=AD=4cm(平行四边形的对边相等。)
∴ ABCD的周长为:6+6+4+4=20(cm)
3.已知:如图,在 ABCD中,BE平分∠ABC交AD于点E
(1)如果AE=2,求CD的长;
(2)如果∠AED=40°,求∠C的度数。
解:(1)∵BE平分∠ABC,并且AD∥BC,
∴∠ABE=∠EBC=∠AEB,
∴AB=AE=2。
又∵CD=AB,∴CD=2。
B
C
D
A
E
(2)由(1)知∠ABE=∠AEB=40°,
∴∠A=180°-(40°+40°)=100°。
又∵∠C=∠A,
∴∠C=100°
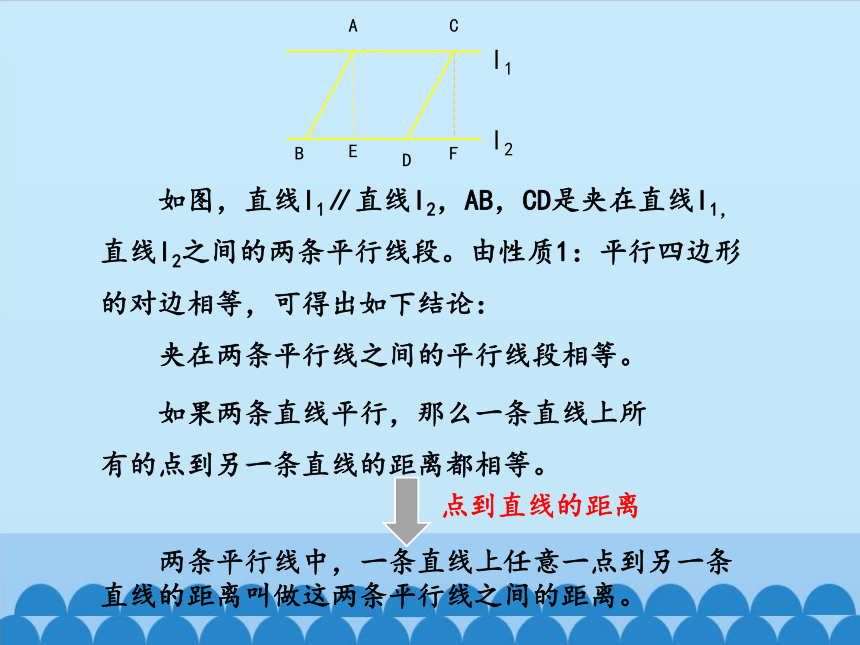
l1
l2
A
C
B
D
E
F
如图,直线l1∥直线l2,AB,CD是夹在直线l1,直线l2之间的两条平行线段。由性质1:平行四边形的对边相等,可得出如下结论:
夹在两条平行线之间的平行线段相等。
如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等。
点到直线的距离
两条平行线中,一条直线上任意一点到另一条直线的距离叫做这两条平行线之间的距离。
推论2:平行线间的距离处处相等。
a
b
A
B
D
C
a
b
A
B
C
D
∵ a // b
AB⊥b,CD⊥b
∴ AB=CD
推论1: 夹在两条平行线间的平行线段相等。
∵ a //b,AB//CD ∴ AB=CD
已知:如图,□ABCD中,AB=4,AD=5,∠B=45°。求直线AD和直线BC之间的距离,直线AB和直线DC之间的距离。
知识应用:
4
5
B
A
C
D
E
F
45°
4
5
B
A
C
D
E
F
45°
解:过点A作AE⊥BC,AF⊥CD,垂足分别为点E和点F,
∴线段AE,AF的长分别为点A到直线BC和直线CD的距离。
∴线段AE的长为直线AD和直线BC之间的距离,线段AF的长为直线AB和直线CD之间的距离。
∵在Rt△ABE中,∠AEB=90°,∠B=45°,AB=4,
∴ ∠B= ∠BAE。
又∵AE2 +AE2=AB2 ∴2AE2=16。
∴AE= 同理AE=
所以直线AD与直线BC之间的距离为 ,直线AB和直线CD之间的距离为 。
如图小明家有一块三角形鱼塘,今年他爸爸把鱼塘扩建,过△ABC的三个顶点,分别作对边的平行线,这三条直线两两相交,得△A′B′C′,这时小明发现并说 △ABC的顶点分别是△A′B′C′三边的中点,你能说明理由吗?
证明:∵AB∥CB′,BC∥AB′
∴AB′=BC
同理:AC′=BC
∴AB′=AC′
同理:BC′=BA′,CA′=CB′
∴△ABC的顶点A、B、C分别是△A′B′C′三边中点。
A
B
C
A′
B′
C′
∴ AD=BC,AD∥BC。
(平行四边形对边平行且相等)
A
C
D
B
已知:如图: ABCD的对角线AC、BD相交于点O。
求证:OA=OC,OB=OD。
O
证明:
∵四边形ABCD是平行四边形
∴∠1=∠2,∠3=∠4。
∴△AOD≌△COB(ASA)。
∴OA=OC,OB=OD。
3
2
4
1
平行四边形性质
性质3:平行四边形的对角线互相平分。
A
D
B
C
∵四边形ABCD是平行四边形。
∴AO=CO, BO=DO
0
几何语言:
已知:如图,在四边形ABCD中,AB=CD,AB∥CD
求证:四边形ABCD是平行四边形
B
C
A
D
证明:
连接DB,∵AB∥CD,
∴∠CDB=∠ABD
在△CDB与△ABD中
CD=AB(已知)
∠CDB=∠ABD(已证)
DB=BD(公共边)
∴△CDB≌△ABD(SAS)
∴∠ADB=∠CBD(全等三角形的对应角相等)
∴AD∥BC(内错角相等,两直线平行)
因此,四边形ABCD是平行四边行。
判定定理1:一组对边平行且相等的四边形是平行四边形。
已知:四边形ABCD,AB=CD,AD=BC
求证:四边形ABCD是平行四边形。
证明:连结AC,
∵在△ABC与△CDA中
AB=CD(已知)
AD=BC(已知)
AC=CA(公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形
B
D
A
C
2
1
3
4
定理2:两组对边分别相等的四边形是平行四边形。
已知:如图,四边形ABCD,AC、BD交于点O且OA=OC,OB=OD
求证:四边形ABCD是平行四边形。
B
D
A
C
O
4
2
1
3
证明:∵在△AOB与△COD中
AO=CO(已知)
∠1=∠2(已知)
BO=DO(已知)
∴△AOB≌△COD(SAS)
∴∠3=∠4
∴AB∥CD
同理AD∥BC
∴四边形ABCD是平行四边形。
定理3:对角线互相平分的四边形是平行四边形。
平行四边形的判定方法
定理1:一组对边平行且相等的四边形是平行四边形。
定理2:两组对边分别相等的四边形是平行四边形。
定理3:对角线互相平分的四边形是平行四边形。
B
C
A
D
已知如图,点E、F是平行四边形对角线AB上的两点,且AE=CF。求证:四边形BEDF是平行四边形。
E
F
O
证明:连接BD交AC于点O。
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO。
又∵AE=CF,
∴OE=OF。
∴四边形BEDF是平行四边形。
1.如图,在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC= cm,CD= cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,那么当AO= cm,DO= cm时,四边形ABCD为平行四边形。
巩固练习
2.如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,EM和FN有怎样的关系?为什么?
巩固练习
B
D
A
C
M
N
E
F
1.连接三角形两边中点的线段叫做三角形的中位线,一个三角形有 条中位线。
2.在练习本上画出一个三角形,并画出它的一条中位线。
三
自主学习
三角形中位线定理
三角形的中位线平行于第三边,且等于第三边的一半。
C
A
B
D
E
用符号语言表示
∵DE是△ABC的中位线
∴ DE∥BC,
数量关系
位置关系
(1)证明平行;
(2)证明一条线段是另一条线
段的2倍或 。
A
B
C
D
E
三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半。
三角形的中位线定理的主要用途:
第三边
1.如图, MN 为△ABC 的中位线,若∠ABC =61°则∠AMN = ,若MN =12 ,则BC = 。
A
M
B
C
N
61°
24
练一练
2.如图,△ABC中,D、E分别为AB、AC的中点,当BC=10㎝时,则DE= 。
A
D
B
C
E
5㎝
说说本节课你学到了什么?
课后练习。
谢 谢
平行四边形
两组对边分别平行的四边形叫做平行四边形。
学一学
A
B
C
D
∵ AD∥BC, AB∥CD
∴四边形ABCD是平行四边形。
几何语言:
用文字和几何语言叙述平行四边形的性质。
平行四边形的对边相等
平行四边形的对边平行
平行四边形的对角相等
平行四边形的邻角互补
A
B
D
C
O
AB=CD;AD=BC
AB∥CD;AD∥BC
∠ABC=∠ADC;∠BAD=∠BCD
∠ABC+∠BCD=180°
如图所示,四边形ABCD是平行四边形
①若周长为30cm,CD=6cm,则AB= cm,BC= cm;AD= cm。
②若∠A=60°,则∠B= 。
∠C= ;∠D= 。
③若∠ B -∠A = 80°,则∠A= ; ∠D= 。
④ ABCD的周长为30cm,两邻边之比为2﹕1,
则ABCD的两邻边长分别为 。
6
9
9
试一试:
C
D
A
B
120°
120°
60°
50°
130°
10cm、5cm
1.这是小明家的楼梯,扶手是用不锈钢管制作的,这些竖直的钢管长度相等吗?
议一议
2.在笔直的铁轨上,夹在两根铁轨之间的枕木是否一样长?
议一议
性质1:平行四边形的对边相等。
A
B
C
D
∵四边形ABCD是平行四边形。∴AB=CD,BC=AD。
几何语言:
性质2:平行四边形的对角相等
A
B
C
D
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
几何语言:
1.在 ABCD中,已知∠A=32°,求其余三个角的度数。
A
B
C
D
∵四边形ABCD是平行四边形
解:
且∠A=32°(已知)
∴∠C=∠A=32°(平行四边形对角相等。) 同理∠B=∠D
又∵AD∥BC(平行四边形的对边平行。)
∴∠A+∠B=180°(两直线平行,同旁内角互补。)
∴∠D=∠B=180°-∠A=180°-32°=148°
2.已知在 ABCD中,AB=6cm,BC=4cm,求 ABCD 的周长。
A
B
C
D
解:∵四边形ABCD是平行四边形(已知)
∴AB=CD=6cm,
BC=AD=4cm(平行四边形的对边相等。)
∴ ABCD的周长为:6+6+4+4=20(cm)
3.已知:如图,在 ABCD中,BE平分∠ABC交AD于点E
(1)如果AE=2,求CD的长;
(2)如果∠AED=40°,求∠C的度数。
解:(1)∵BE平分∠ABC,并且AD∥BC,
∴∠ABE=∠EBC=∠AEB,
∴AB=AE=2。
又∵CD=AB,∴CD=2。
B
C
D
A
E
(2)由(1)知∠ABE=∠AEB=40°,
∴∠A=180°-(40°+40°)=100°。
又∵∠C=∠A,
∴∠C=100°
l1
l2
A
C
B
D
E
F
如图,直线l1∥直线l2,AB,CD是夹在直线l1,直线l2之间的两条平行线段。由性质1:平行四边形的对边相等,可得出如下结论:
夹在两条平行线之间的平行线段相等。
如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等。
点到直线的距离
两条平行线中,一条直线上任意一点到另一条直线的距离叫做这两条平行线之间的距离。
推论2:平行线间的距离处处相等。
a
b
A
B
D
C
a
b
A
B
C
D
∵ a // b
AB⊥b,CD⊥b
∴ AB=CD
推论1: 夹在两条平行线间的平行线段相等。
∵ a //b,AB//CD ∴ AB=CD
已知:如图,□ABCD中,AB=4,AD=5,∠B=45°。求直线AD和直线BC之间的距离,直线AB和直线DC之间的距离。
知识应用:
4
5
B
A
C
D
E
F
45°
4
5
B
A
C
D
E
F
45°
解:过点A作AE⊥BC,AF⊥CD,垂足分别为点E和点F,
∴线段AE,AF的长分别为点A到直线BC和直线CD的距离。
∴线段AE的长为直线AD和直线BC之间的距离,线段AF的长为直线AB和直线CD之间的距离。
∵在Rt△ABE中,∠AEB=90°,∠B=45°,AB=4,
∴ ∠B= ∠BAE。
又∵AE2 +AE2=AB2 ∴2AE2=16。
∴AE= 同理AE=
所以直线AD与直线BC之间的距离为 ,直线AB和直线CD之间的距离为 。
如图小明家有一块三角形鱼塘,今年他爸爸把鱼塘扩建,过△ABC的三个顶点,分别作对边的平行线,这三条直线两两相交,得△A′B′C′,这时小明发现并说 △ABC的顶点分别是△A′B′C′三边的中点,你能说明理由吗?
证明:∵AB∥CB′,BC∥AB′
∴AB′=BC
同理:AC′=BC
∴AB′=AC′
同理:BC′=BA′,CA′=CB′
∴△ABC的顶点A、B、C分别是△A′B′C′三边中点。
A
B
C
A′
B′
C′
∴ AD=BC,AD∥BC。
(平行四边形对边平行且相等)
A
C
D
B
已知:如图: ABCD的对角线AC、BD相交于点O。
求证:OA=OC,OB=OD。
O
证明:
∵四边形ABCD是平行四边形
∴∠1=∠2,∠3=∠4。
∴△AOD≌△COB(ASA)。
∴OA=OC,OB=OD。
3
2
4
1
平行四边形性质
性质3:平行四边形的对角线互相平分。
A
D
B
C
∵四边形ABCD是平行四边形。
∴AO=CO, BO=DO
0
几何语言:
已知:如图,在四边形ABCD中,AB=CD,AB∥CD
求证:四边形ABCD是平行四边形
B
C
A
D
证明:
连接DB,∵AB∥CD,
∴∠CDB=∠ABD
在△CDB与△ABD中
CD=AB(已知)
∠CDB=∠ABD(已证)
DB=BD(公共边)
∴△CDB≌△ABD(SAS)
∴∠ADB=∠CBD(全等三角形的对应角相等)
∴AD∥BC(内错角相等,两直线平行)
因此,四边形ABCD是平行四边行。
判定定理1:一组对边平行且相等的四边形是平行四边形。
已知:四边形ABCD,AB=CD,AD=BC
求证:四边形ABCD是平行四边形。
证明:连结AC,
∵在△ABC与△CDA中
AB=CD(已知)
AD=BC(已知)
AC=CA(公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形
B
D
A
C
2
1
3
4
定理2:两组对边分别相等的四边形是平行四边形。
已知:如图,四边形ABCD,AC、BD交于点O且OA=OC,OB=OD
求证:四边形ABCD是平行四边形。
B
D
A
C
O
4
2
1
3
证明:∵在△AOB与△COD中
AO=CO(已知)
∠1=∠2(已知)
BO=DO(已知)
∴△AOB≌△COD(SAS)
∴∠3=∠4
∴AB∥CD
同理AD∥BC
∴四边形ABCD是平行四边形。
定理3:对角线互相平分的四边形是平行四边形。
平行四边形的判定方法
定理1:一组对边平行且相等的四边形是平行四边形。
定理2:两组对边分别相等的四边形是平行四边形。
定理3:对角线互相平分的四边形是平行四边形。
B
C
A
D
已知如图,点E、F是平行四边形对角线AB上的两点,且AE=CF。求证:四边形BEDF是平行四边形。
E
F
O
证明:连接BD交AC于点O。
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO。
又∵AE=CF,
∴OE=OF。
∴四边形BEDF是平行四边形。
1.如图,在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC= cm,CD= cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,那么当AO= cm,DO= cm时,四边形ABCD为平行四边形。
巩固练习
2.如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,EM和FN有怎样的关系?为什么?
巩固练习
B
D
A
C
M
N
E
F
1.连接三角形两边中点的线段叫做三角形的中位线,一个三角形有 条中位线。
2.在练习本上画出一个三角形,并画出它的一条中位线。
三
自主学习
三角形中位线定理
三角形的中位线平行于第三边,且等于第三边的一半。
C
A
B
D
E
用符号语言表示
∵DE是△ABC的中位线
∴ DE∥BC,
数量关系
位置关系
(1)证明平行;
(2)证明一条线段是另一条线
段的2倍或 。
A
B
C
D
E
三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半。
三角形的中位线定理的主要用途:
第三边
1.如图, MN 为△ABC 的中位线,若∠ABC =61°则∠AMN = ,若MN =12 ,则BC = 。
A
M
B
C
N
61°
24
练一练
2.如图,△ABC中,D、E分别为AB、AC的中点,当BC=10㎝时,则DE= 。
A
D
B
C
E
5㎝
说说本节课你学到了什么?
课后练习。
谢 谢
