北师大版八年级下册6.1.1平行四边形的性质课件(共17张PPT)
文档属性
| 名称 | 北师大版八年级下册6.1.1平行四边形的性质课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 06:33:23 | ||
图片预览



文档简介
(共17张PPT)
6.1平行四边形的性质(1)
课题
观察感知
以上图中有哪种我们熟悉的图形?你还能举出一些实例吗?
学生举例
还比如校园的伸缩门,楼梯的扶手,窗户等。
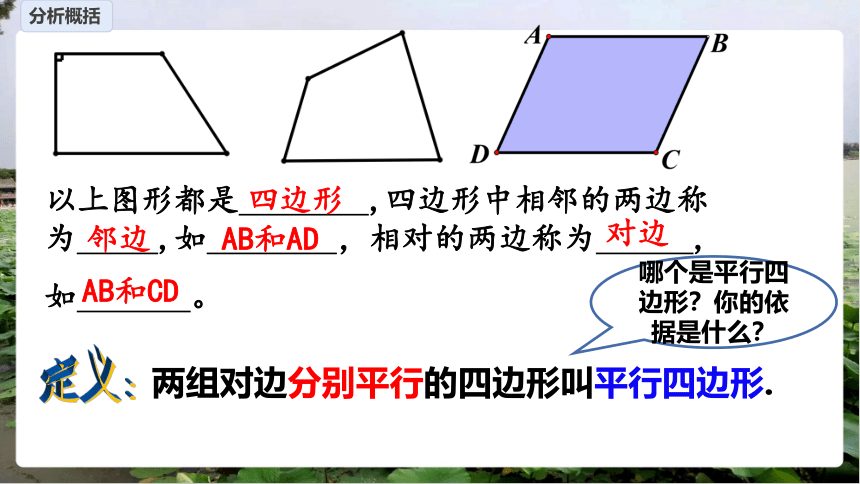
哪个是平行四边形?你的依据是什么?
分析概括
以上图形都是 ,四边形中相邻的两边称为 ,如 ,相对的两边称为 ,
如 。
两组对边分别平行的四边形叫平行四边形.
定义:
四边形
邻边
对边
AB和AD
AB和CD
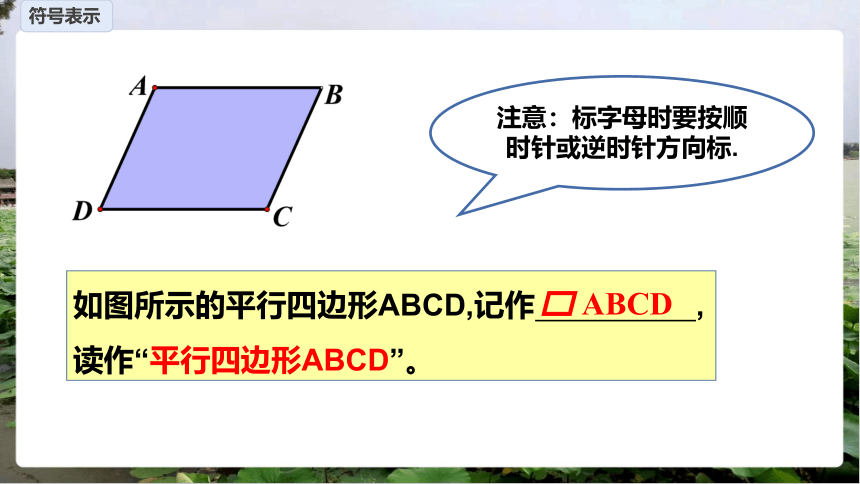
符号表示
如图所示的平行四边形ABCD,记作 ,读作“平行四边形ABCD”。
ABCD
注意:标字母时要按顺时针或逆时针方向标.
两组对边分别平行的四边形叫平行四边形.
定义:
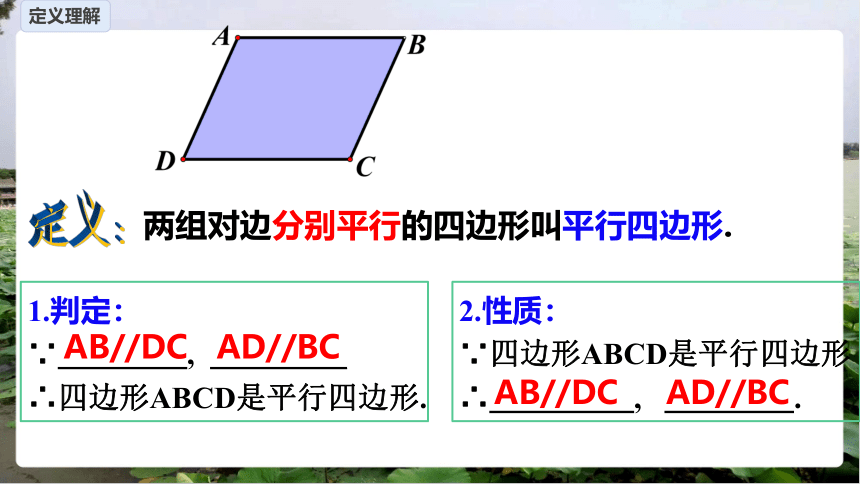
1.判定:
∵ , 。
∴四边形ABCD是平行四边形.
2.性质:
∵四边形ABCD是平行四边形
∴ , .
AB//DC AD//BC
定义理解
AB//DC AD//BC
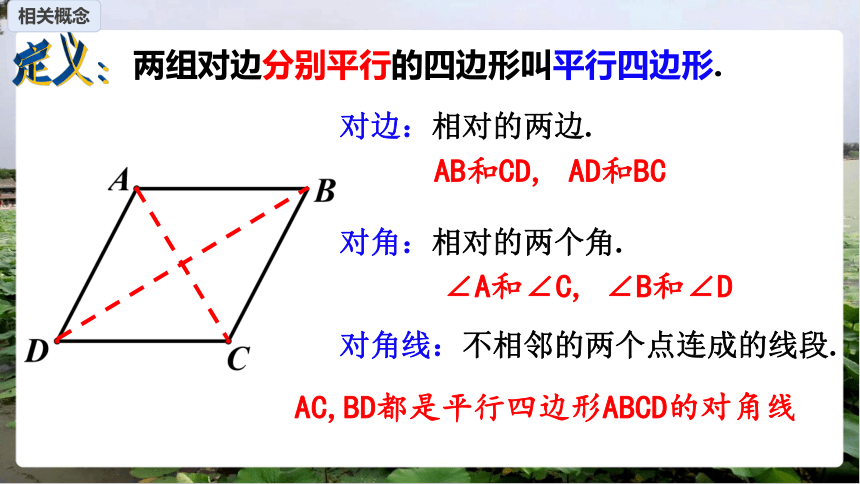
两组对边分别平行的四边形叫平行四边形.
定义:
对边:相对的两边.
对角:相对的两个角.
对角线:不相邻的两个点连成的线段.
相关概念
AB和CD,
AD和BC
∠A和∠C,
∠B和∠D
AC,BD都是平行四边形ABCD的对角线
证明:连接AC,∵ ABCD
∴ // , // ,
∴ = , = .
∴ .
∴ 在△ABC和△CDA中,
= , AC = CA , = .
∴ △ABC≌△CDA( )
∴ AB=DC, AD=CB, ∠B=∠D
1.探究一:平行四边的对边 ,对角 .
已知: ABCD,
求证:AB=CD,BC=AD,∠B=∠D,∠BAD=∠BCD
相等
AB DC AD BC
∠BAC ∠DCA
∠DAC ∠BCA
∠BAC ∠DCA
∠DAC ∠BCA
ASA
相等
∠BAD=∠BCD
(1)∵ ABCD ∴ , . (2)∵ ABCD
∴ , .
平行四边形的对边相等;
性质1:
对角相等.
性质2:
性质总结
符号表示
AB=DC
∠A=∠C
∠B=∠D
AD=BC
例1.如图,四边形ABCD是平行四边形。则(1)∠ADC=_______,∠BCD=_________;(2)AB=________,BC=__________。
70°
110°
40
50
学以致用
2.探究二:□ABCD是中心对称图形吗?如果是你能找出他的对称中心并验证你的结论吗?
平行四边形是________________图形,
对称中心是_______________________.
性质3:
中心对称
两条对角线的交点
对应点的连线经过对称中心,故对称中心是O.
例2.己知,在□ABCD中,E,F是对角线AC上的两点,且AE=CF,求证:DE=BF。证明:
在△ADE与△CBF中,
AD=BC
∠1=∠2
∴△ADE≌△CBF(SAS)
∴DE=BF
AE=CF
∴AD = BC
∵ ABCD
当堂练习
∴∠C=∠A=48°
∠B=∠D=180°-48°=132°
AD=BC=3cm
解:∵ ABCD
1.在平行四边形ABCD中,∠A=48°,BC=3cm,求∠B,∠C的度数及AD边的长度.
当堂练习
∴∠B=∠D=125°
∴∠CAB=∠ACD=180°-21°-125°=34°
AB//DC
解:∵ ABCD
2.如图,在平行四边形ABCD中,∠ADC=125°,∠CAD=21°,求∠ABC和∠CAB的度数。
当堂练习
AB=DC
∠B=∠D
∴△ABE≌△CDF(SAS)
∴AB = DC,
BE=DF
∠B = ∠D
在△ABE与△CDF中,
证明:∵ ABCD
3.已知:如图,在平行四边形ABCD中,E,F分别是 BC和AD上的点,且BE=DF.
求证:ΔABE≌ACDF
AD=BC
∴△ADF≌△CBE(SAS)
∴AF=CE
∴AD = BC,
∠A = ∠C,
∠ADC = ∠ABC,
又∵DF平分∠ADC,BE平分∠ABC,
∴∠ADF = ∠EBC,
∠A = ∠C,
∠ADF = ∠EBC,
∴AB-AF=DC-CE
AB = DC,
∴BF=DE
在△ADF与△CBE中,
4.已知:如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.求证:BF=DE.
证明:∵ ABCD
归纳总结
本节课你学到了什么?
平行四边形
定义:两组对边分别平行的四边形叫平行四边形.
记作: ABCD
性质:①对边平行且相等;
②对角相等.
6.1平行四边形的性质(1)
课题
观察感知
以上图中有哪种我们熟悉的图形?你还能举出一些实例吗?
学生举例
还比如校园的伸缩门,楼梯的扶手,窗户等。
哪个是平行四边形?你的依据是什么?
分析概括
以上图形都是 ,四边形中相邻的两边称为 ,如 ,相对的两边称为 ,
如 。
两组对边分别平行的四边形叫平行四边形.
定义:
四边形
邻边
对边
AB和AD
AB和CD
符号表示
如图所示的平行四边形ABCD,记作 ,读作“平行四边形ABCD”。
ABCD
注意:标字母时要按顺时针或逆时针方向标.
两组对边分别平行的四边形叫平行四边形.
定义:
1.判定:
∵ , 。
∴四边形ABCD是平行四边形.
2.性质:
∵四边形ABCD是平行四边形
∴ , .
AB//DC AD//BC
定义理解
AB//DC AD//BC
两组对边分别平行的四边形叫平行四边形.
定义:
对边:相对的两边.
对角:相对的两个角.
对角线:不相邻的两个点连成的线段.
相关概念
AB和CD,
AD和BC
∠A和∠C,
∠B和∠D
AC,BD都是平行四边形ABCD的对角线
证明:连接AC,∵ ABCD
∴ // , // ,
∴ = , = .
∴ .
∴ 在△ABC和△CDA中,
= , AC = CA , = .
∴ △ABC≌△CDA( )
∴ AB=DC, AD=CB, ∠B=∠D
1.探究一:平行四边的对边 ,对角 .
已知: ABCD,
求证:AB=CD,BC=AD,∠B=∠D,∠BAD=∠BCD
相等
AB DC AD BC
∠BAC ∠DCA
∠DAC ∠BCA
∠BAC ∠DCA
∠DAC ∠BCA
ASA
相等
∠BAD=∠BCD
(1)∵ ABCD ∴ , . (2)∵ ABCD
∴ , .
平行四边形的对边相等;
性质1:
对角相等.
性质2:
性质总结
符号表示
AB=DC
∠A=∠C
∠B=∠D
AD=BC
例1.如图,四边形ABCD是平行四边形。则(1)∠ADC=_______,∠BCD=_________;(2)AB=________,BC=__________。
70°
110°
40
50
学以致用
2.探究二:□ABCD是中心对称图形吗?如果是你能找出他的对称中心并验证你的结论吗?
平行四边形是________________图形,
对称中心是_______________________.
性质3:
中心对称
两条对角线的交点
对应点的连线经过对称中心,故对称中心是O.
例2.己知,在□ABCD中,E,F是对角线AC上的两点,且AE=CF,求证:DE=BF。证明:
在△ADE与△CBF中,
AD=BC
∠1=∠2
∴△ADE≌△CBF(SAS)
∴DE=BF
AE=CF
∴AD = BC
∵ ABCD
当堂练习
∴∠C=∠A=48°
∠B=∠D=180°-48°=132°
AD=BC=3cm
解:∵ ABCD
1.在平行四边形ABCD中,∠A=48°,BC=3cm,求∠B,∠C的度数及AD边的长度.
当堂练习
∴∠B=∠D=125°
∴∠CAB=∠ACD=180°-21°-125°=34°
AB//DC
解:∵ ABCD
2.如图,在平行四边形ABCD中,∠ADC=125°,∠CAD=21°,求∠ABC和∠CAB的度数。
当堂练习
AB=DC
∠B=∠D
∴△ABE≌△CDF(SAS)
∴AB = DC,
BE=DF
∠B = ∠D
在△ABE与△CDF中,
证明:∵ ABCD
3.已知:如图,在平行四边形ABCD中,E,F分别是 BC和AD上的点,且BE=DF.
求证:ΔABE≌ACDF
AD=BC
∴△ADF≌△CBE(SAS)
∴AF=CE
∴AD = BC,
∠A = ∠C,
∠ADC = ∠ABC,
又∵DF平分∠ADC,BE平分∠ABC,
∴∠ADF = ∠EBC,
∠A = ∠C,
∠ADF = ∠EBC,
∴AB-AF=DC-CE
AB = DC,
∴BF=DE
在△ADF与△CBE中,
4.已知:如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.求证:BF=DE.
证明:∵ ABCD
归纳总结
本节课你学到了什么?
平行四边形
定义:两组对边分别平行的四边形叫平行四边形.
记作: ABCD
性质:①对边平行且相等;
②对角相等.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
