9.2.4总体离散程度的估计 课件(共31张PPT)
文档属性
| 名称 | 9.2.4总体离散程度的估计 课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 06:58:49 | ||
图片预览








文档简介
(共31张PPT)
9.2.4 总体离散程度的估计
一、导入
上节课我们学均数、中位数、众数
1)平均数:如果有n个数据 那么这n个数的平均数
从频率分布直方图中估计平均数:
平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
一、导入
2)中位数:把一组数据按大小顺序排列,处在最中间的一个数据(或两个数据的平均数);
从频率分布直方图中估计中位数:中位数左右两边的直方图的面积相等.
3)众数:一组数据中重复出现次数最多的数;
从频率分布直方图中估计众数:众数是最高的矩形的中点.
一、导入
平均数、中位数和众数为我们提供了一组数据的集中趋势的信息,这是概括一组数据的特征的有效方法.
但仅知道集中趋势的信息,很多时候还不能使我们做出有效的决策.
这节课学习数据的另一大重要特征:离散程度
一、导入
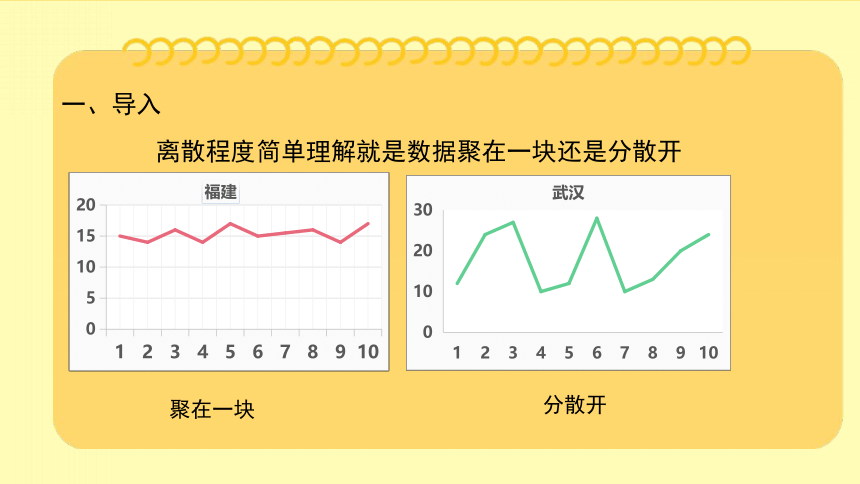
离散程度简单理解就是数据聚在一块还是分散开
聚在一块
分散开
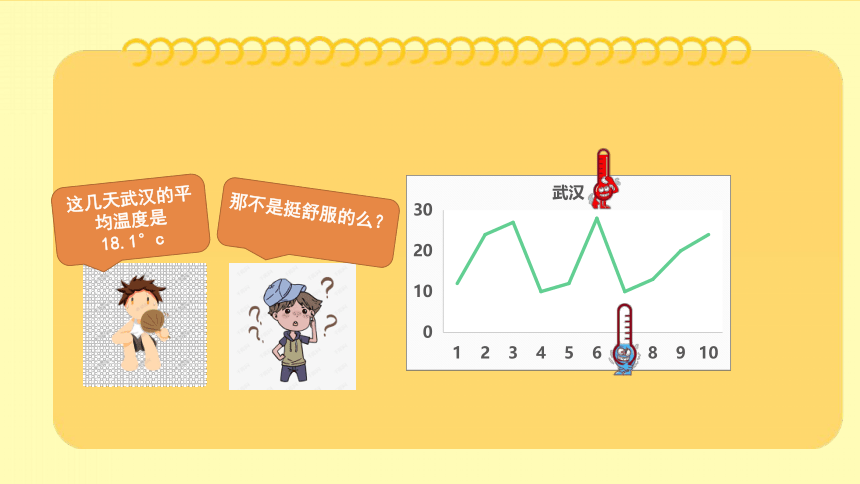
这几天武汉的平均温度是18.1°c
那不是挺舒服的么?
整齐
稳定
稳定,整齐就是离散程度低的意思
一、导入
初中用方差和标准差来衡量一组数据的离散程度
方差,标准差大
离散程度大
方差,标准差小
离散程度小
一、导入
计算方差和标准差:
1)求平均数
数据:
2)数据与平均数作差
3)平方
4)求平方的平均数
二、新课讲授
问题1:有两名射击队员在一次射击测试中各射靶10次,每次命中的环数如下:
甲 7 8 7 9 5 4 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
如果你是教练,你如何对两位运动员的射击情况作出评价?如果这是一次选拔性考核,你应当如何作出选择?
二、新课讲授
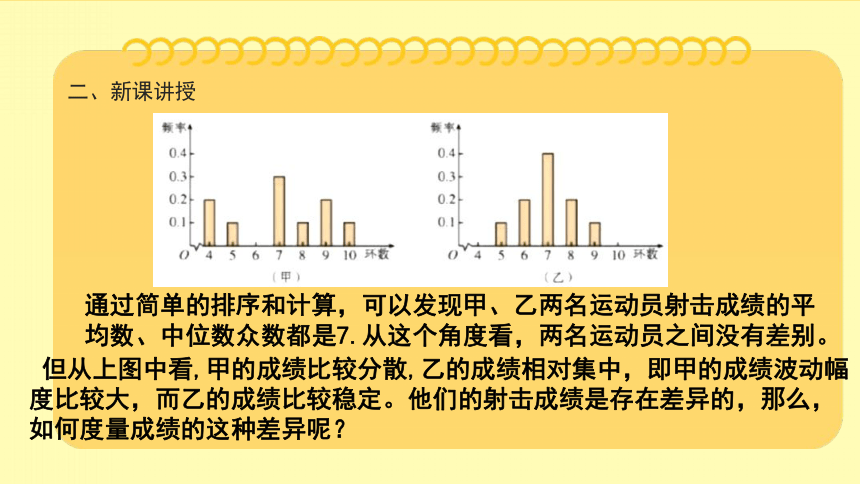
通过简单的排序和计算,可以发现甲、乙两名运动员射击成绩的平均数、中位数众数都是7.从这个角度看,两名运动员之间没有差别。
但从上图中看,甲的成绩比较分散,乙的成绩相对集中,即甲的成绩波动幅度比较大,而乙的成绩比较稳定。他们的射击成绩是存在差异的,那么,如何度量成绩的这种差异呢?
二、新课讲授
一种简单的度量数据离散程度的方法就是用极差。
根据甲、乙运动员的10次射击成绩,可以得到
甲命中环数的极差=10-4=6
乙命中环数的极差=9-5=4
可以发现甲的成绩波动范围比乙大。极差在一定程度上刻画了数据的离散程度,但因为极差只使用了数据中最大、最小两个值的信息,对其他数据的取值情况没有涉及,所以极差所含的信息量很少。
二、新课讲授
你还能想出其他刻画数据离散程度的办法么?
二、新课讲授
我们知道,如果射击的成绩很稳定,那么大多数的射击成绩离平均成绩不会太远;
相反,如果射击的成绩波动幅度很大,那么大多数的射击成绩离平均成绩会比较远。
因此,我们可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度。
二、新课讲授
如何定义“平均距离”?
二、新课讲授
假设一组数据是 ,用 表示这组数据的平均数。
用每个数据与平均数的差的绝对值作为“距离”,即
则这组数据到 的“平均距离”为
为了避免式中含有绝对值,通常改用平方来代替,即
我们将其定义为这组数据的方差:
二、新课讲授
有时为了计算方差的方便,我们还把方差写成以下形式
二、新课讲授
由于方差的单位是原始数据的单位的平方,与原始数据不一致。为了使二者单位一致,我们对方差开方,取它的算数平方根,即
我们称其为这组数据的标准差
二、新课讲授
1.总体方差和总体标准差
(1)若总体中所有个体的变量值分别为Y1,Y2,…,YN,总体的平均
数为 ,则称 为总体方差, 为总体标准差.
(2)总体方差的加权形式:如果总体的N个变量值中,不同的值共有k(k≤N)个,可以记为Y1,Y2,…,Yk,其中Yi出现的频数为
fi(i=1,2,…,k),则总体方差为
二、新课讲授
2.样本方差和样本标准差
若一个样本中个体的变量值分别为y1,y2,....,yn,
总体平均数为 ,则称
为样本方差,
为样本标准差
标准差刻画了数据的数据的离散程度或波动幅度,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小; 显然,在刻画数据的分散程度上,方差和标准差是一样的,但在解决实际问题中,一般多采用标准差。
二、新课讲授
问题1:有两名射击队员在一次射击测试中各射靶10次,每次命中的环数如下:
甲 7 8 7 9 5 4 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
如果你是教练,你如何对两位运动员的射击情况作出评价?如果这是一次选拔性考核,你应当如何作出选择?
即乙比甲的射击成绩稳定
例1 甲、乙两机床同时加工直径为100 cm的零件,为检验质量,从中抽取6件测量数据为(单位:cm):
甲:99 100 98 100 100 103
乙:99 100 102 99 100 100
(1) 分别计算两组数据的平均数及方差;
(2) 根据计算说明哪台机床加工零件的质量更稳定.
变式1 样本数均为9的四组数据,它们的平均数都是5,条形图如图所示,则标准差最大的一组是( )
A.第一组 B.第二组 C.第三组 D.第四组
总结:平均数、方差性质
总结:平均数、方差性质
归纳小结,回顾重点
9.2.4 总体离散程度的估计
一、导入
上节课我们学均数、中位数、众数
1)平均数:如果有n个数据 那么这n个数的平均数
从频率分布直方图中估计平均数:
平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
一、导入
2)中位数:把一组数据按大小顺序排列,处在最中间的一个数据(或两个数据的平均数);
从频率分布直方图中估计中位数:中位数左右两边的直方图的面积相等.
3)众数:一组数据中重复出现次数最多的数;
从频率分布直方图中估计众数:众数是最高的矩形的中点.
一、导入
平均数、中位数和众数为我们提供了一组数据的集中趋势的信息,这是概括一组数据的特征的有效方法.
但仅知道集中趋势的信息,很多时候还不能使我们做出有效的决策.
这节课学习数据的另一大重要特征:离散程度
一、导入
离散程度简单理解就是数据聚在一块还是分散开
聚在一块
分散开
这几天武汉的平均温度是18.1°c
那不是挺舒服的么?
整齐
稳定
稳定,整齐就是离散程度低的意思
一、导入
初中用方差和标准差来衡量一组数据的离散程度
方差,标准差大
离散程度大
方差,标准差小
离散程度小
一、导入
计算方差和标准差:
1)求平均数
数据:
2)数据与平均数作差
3)平方
4)求平方的平均数
二、新课讲授
问题1:有两名射击队员在一次射击测试中各射靶10次,每次命中的环数如下:
甲 7 8 7 9 5 4 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
如果你是教练,你如何对两位运动员的射击情况作出评价?如果这是一次选拔性考核,你应当如何作出选择?
二、新课讲授
通过简单的排序和计算,可以发现甲、乙两名运动员射击成绩的平均数、中位数众数都是7.从这个角度看,两名运动员之间没有差别。
但从上图中看,甲的成绩比较分散,乙的成绩相对集中,即甲的成绩波动幅度比较大,而乙的成绩比较稳定。他们的射击成绩是存在差异的,那么,如何度量成绩的这种差异呢?
二、新课讲授
一种简单的度量数据离散程度的方法就是用极差。
根据甲、乙运动员的10次射击成绩,可以得到
甲命中环数的极差=10-4=6
乙命中环数的极差=9-5=4
可以发现甲的成绩波动范围比乙大。极差在一定程度上刻画了数据的离散程度,但因为极差只使用了数据中最大、最小两个值的信息,对其他数据的取值情况没有涉及,所以极差所含的信息量很少。
二、新课讲授
你还能想出其他刻画数据离散程度的办法么?
二、新课讲授
我们知道,如果射击的成绩很稳定,那么大多数的射击成绩离平均成绩不会太远;
相反,如果射击的成绩波动幅度很大,那么大多数的射击成绩离平均成绩会比较远。
因此,我们可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度。
二、新课讲授
如何定义“平均距离”?
二、新课讲授
假设一组数据是 ,用 表示这组数据的平均数。
用每个数据与平均数的差的绝对值作为“距离”,即
则这组数据到 的“平均距离”为
为了避免式中含有绝对值,通常改用平方来代替,即
我们将其定义为这组数据的方差:
二、新课讲授
有时为了计算方差的方便,我们还把方差写成以下形式
二、新课讲授
由于方差的单位是原始数据的单位的平方,与原始数据不一致。为了使二者单位一致,我们对方差开方,取它的算数平方根,即
我们称其为这组数据的标准差
二、新课讲授
1.总体方差和总体标准差
(1)若总体中所有个体的变量值分别为Y1,Y2,…,YN,总体的平均
数为 ,则称 为总体方差, 为总体标准差.
(2)总体方差的加权形式:如果总体的N个变量值中,不同的值共有k(k≤N)个,可以记为Y1,Y2,…,Yk,其中Yi出现的频数为
fi(i=1,2,…,k),则总体方差为
二、新课讲授
2.样本方差和样本标准差
若一个样本中个体的变量值分别为y1,y2,....,yn,
总体平均数为 ,则称
为样本方差,
为样本标准差
标准差刻画了数据的数据的离散程度或波动幅度,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小; 显然,在刻画数据的分散程度上,方差和标准差是一样的,但在解决实际问题中,一般多采用标准差。
二、新课讲授
问题1:有两名射击队员在一次射击测试中各射靶10次,每次命中的环数如下:
甲 7 8 7 9 5 4 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
如果你是教练,你如何对两位运动员的射击情况作出评价?如果这是一次选拔性考核,你应当如何作出选择?
即乙比甲的射击成绩稳定
例1 甲、乙两机床同时加工直径为100 cm的零件,为检验质量,从中抽取6件测量数据为(单位:cm):
甲:99 100 98 100 100 103
乙:99 100 102 99 100 100
(1) 分别计算两组数据的平均数及方差;
(2) 根据计算说明哪台机床加工零件的质量更稳定.
变式1 样本数均为9的四组数据,它们的平均数都是5,条形图如图所示,则标准差最大的一组是( )
A.第一组 B.第二组 C.第三组 D.第四组
总结:平均数、方差性质
总结:平均数、方差性质
归纳小结,回顾重点
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
