第6章 实数 复习课件(共32张PPT)
图片预览










文档简介
(共32张PPT)
沪科版 七年级下册
第6章 实数 复习课件
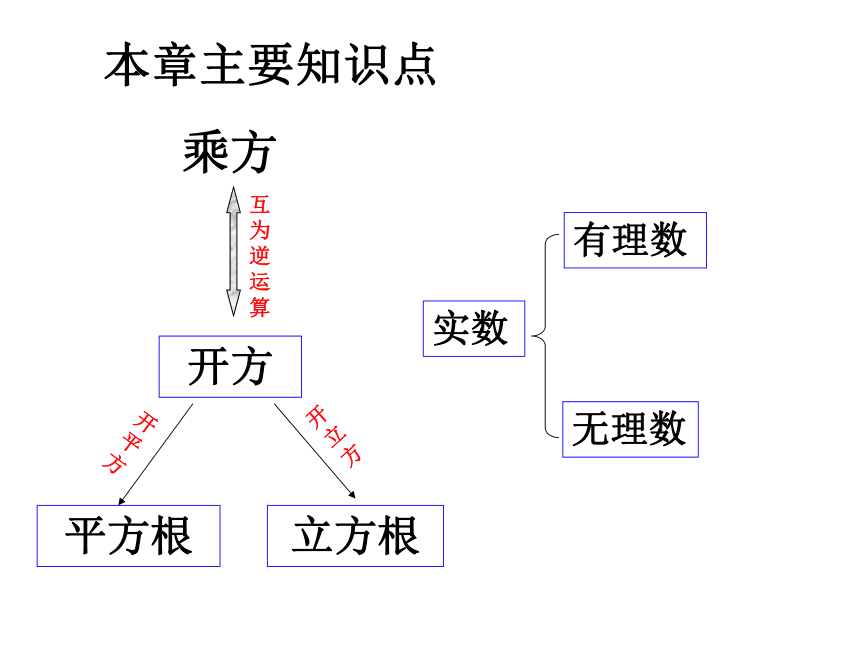
乘方
开方
平方根
立方根
实数
有理数
无理数
互为逆运算
开平方
开立方
本章主要知识点
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根,这就是说,如果x2=a,那么x叫做a的平方根.
1.平方根定义
x= 中,a≥0, ≥0。
非负数a的平方根用符号“± ” 表示,读作:“正、负根号a”。
一般地,如果一个正数x 的平方等于a,即 x2=a,那么这个正数x 叫做a的算术平方根.
a的算术平方根记为:
读作:“根号a”, a叫做被开方数.
2.算术平方根
规定:0 的算术平方根是 0.
也就是说,负数不存在算术平方根。
正数有两个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根.
3.平方根的性质:
4.平方根的记法:
(1) 表示非负数a的正的平方根,
- 表示非负数a的负的平方根;
(2)± 表示非负数a的平方根,
与 - 互为相反数;
(3) 在± 中,a≥0。
一般地,如果一个数的立方等于 a,那么这个数就叫做 a 的立方根或三次方根。即:如果 x3 = a,那么x叫做 a 的立方根.
33 =27,所以3是27的立方根.
5.立方根的定义:
如果 x3 = a ,则 x 叫做 a 的立方根。
记作:x= , 读作“三次根号a”.
6.立方根的性质:
注意: (1)任何数的立方根有且只有一个; (2)一个数a与 同号; (3)互为相反数的两个数的立方根也互为相反数。
a>0,则 >0
a<0,则 <0;
a=0,则 =0。
正数的立方根是正数;
负数的立方根是负数;
0的立方根是0。
算术平方根、平方根、立方根联系和区别
算术平方根 平方根 立方根
表示方法
a的取值
性
质
开方
a≥0
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
是本身
0,1
0
0,1,-1
a≥0
a是任何数
a
a
3
a
±
7.实数的分类
实数
整数
分数
正整数
负整数
负分数
正分数
正无理数
负无理数
有限小数或循环小数
无限不循环小数
有理数
无理数
实数还可分为正实数、0、负实数。
无理数含3类:1.一般形式;2.特殊结构;3.特定含义
0
(一)算术平方根、平方根、立方根典型例析
例1.已知2m -1的平方根是±3,3m+n-1的算术平方根是4,求n-2m的立方根.
∵2m-1的平方根是± 3,
解:
而9的平方根是± 3,
∴2m-1=9,
∴m=5.
∵3m+n-1的算术平方根是4,
而16的算术平方根是4,
∴3m+n-1=16,
∴3×5+n-1=16,
∴n=2
∴n-2m=2-2×5
=-8
∵-8的立方根是-2,
∴n-2m的立方根为-2.
例2.已知: 2m-1 + m+7 =0,
求-2m的平方根.
3
3
∵ 互为相反数的和为0,
∴2m-1 + m+7 =0.
∴m=-2.
∴-2m=4.
∵4平方根是± 2,
∴-2m的平方根为±2.
解:
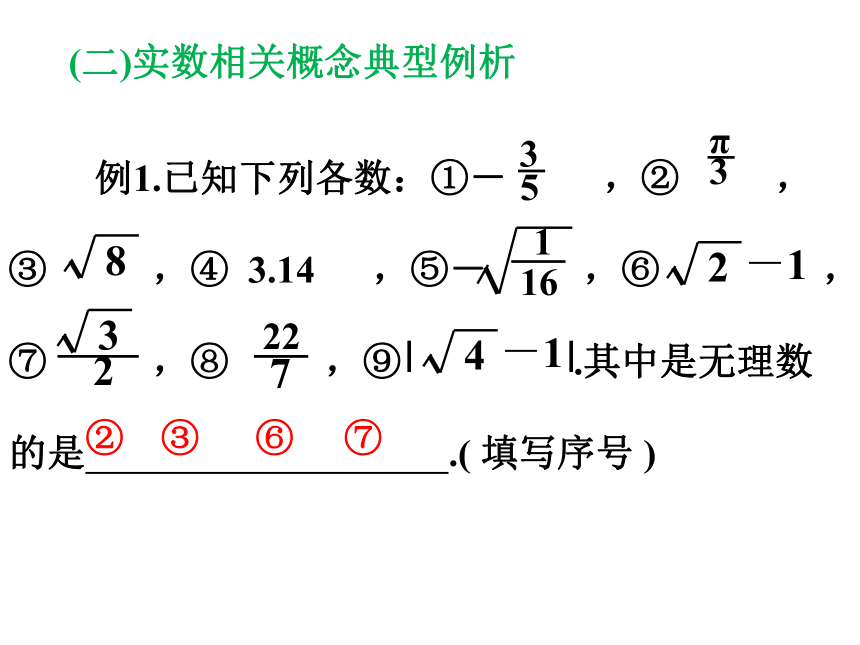
(二)实数相关概念典型例析
例1.已知下列各数:①- ,② ,
③ ,④ 3.14 ,⑤- ,⑥ ,⑦ ,⑧ ,⑨ .其中是无理数的是 .( 填写序号 )
3
5
π
3
1
16
2
-1
3
2
8
22
7
4
-1
| |
②
③
⑥
⑦
例2.比较 与 大小:
解:
3
5
2
5
-
1
3
5
>
∴
2
5
-
1
解法一,作差法
∵125>121,
∴
125
121,
>
∴5
5
11,
>
∴5
5
-11 ,
>0
2
5
-
1
∴
-
3
5
=
10
-
6
10
5
5
-5
=
10
5
5
-11
>0
例2.比较 与 大小:
解:
3
5
2
2.236
-
1
2
5
-
1
≈
≈0.618
3
5
=0.6
2
5
-
1
3
5
>
∴
2
5
-
1
解法二,利用计算器
例3.已知 的整数部分为a,小数部分为b.
求代数式a2-a-b的值.
13
解:
∵
13
3<
<4,
∴a=3,
b= -3
13
∴a2-a-b=
32
-3
-(
13
-3)
=9
-3
13
+3
-
=9-
13
(三)实数的运算典型例析
计算:(1) 3
2
(精确到0.01);
+
5
-
1
2
π
解:
原式≈
3×1.414
+2.236
- ×3.142
1
2
=4.242
+2.236
-1.571
=4.907
≈4.91
(注意:取无理数的近似值时,一般要比要求的精确度多取一位小数)
(三)实数的运算典型例析
计算:(2) -
49
+
2
1
4
64
3
+
解:
原式=
-7
+
3
2
+
4
=
-
3
2
已知
+ =0,
a+b-3
2a-b+6
求 a,b 的值.
(四)实数的非负性典型例析
解:
∵
+ =0,
a+b-3
2a-b+6
∴
2a-b+6=0
a+b-3=0
∴
2a-b=-6
a+b=3
∴
b=4
a=-1
64
±8
8
-4
3.
2.
1.
5.
6.
如果一个数的平方根为a+1和2a-7,
这个数为 .
9
4.
知识点过关练习
A .无限小数是无理数 ;
B .绝对值等于本身的数是正数;
C .实数和数轴上的点一一对应;
D .带根号的数是无理数.
7.下列叙述正确的是( )
C
8.下列说法中,错误的个数是 ( )
①无理数都是无限小数;
②无理数都是开方开不尽的数;
③带根号的都是无理数;
④无限小数都是无理数。
A.1个 B.2个 C.3个 D.4个
C
9.已知按规律排列的一列数: , , , ,
, , …,那么第6个数是 ,
在前6个数中,无理数共有 个
3
6
9
12
15
5
10.适合- < a<
的整数有 .
6
18
5
-2,-1,0,1,2
11.小明编写了一个程序:
输入x →x2 →立方根 → 倒数→
算术平方根 → ,则x为 .
1
2
12.若n= -6,则估计的值所在范围,
下列最接近的是( ).
8
A.4<
<5
n
B.3<
<4
n
C.2<
<3
n
D.1<
<2
n
59
D
13.已知正实数a的平方根是2m+3和n-4,且m-2n=3.求m的值.
正实数a的平方根是2m+3和n-4
解:
∴2m+3+n-4=0
∴2m+n=1
∴
m-2n=3
2m+n=1
∴
m=1
14.已知a是最大的负整数,b是 的小数部分,
c是 的相反数,d没有倒数.
求 的值.
3
2022
3
| a-b |+-
3
2
cd
解:
∵a是最大的负整数,
∴a= -1,
∵b是 的小数部分,
∵c是 的相反数,
∵d没有倒数,
∴c=- ,
∴d=0 .
∴| a-b |+ cd
3
2
∴b= -1,
3
2022
3
2022
3
|-1-( -1)|+ ×(- )×0
3
2
=
2022
3
3
3
=
3
15.设2 + 的整数部分为a,小数部分为b.
(1)求2a+1的平方根;(2)化简:
6
解:(1)
∵
6
2<
<3,
∴a=4,
b= -2
6
| b-2 |.
∴2 +2
<
2+
6
<3+2
∴4<
2+
6
<5
∴2a+1=2 ×4 +1
=9
∵9平方根是±3,
∴2a+1的平方根是±3.
15.设2 + 的整数部分为a,小数部分为b.
(1)求2a+1的平方根;(2)化简:
6
解:(2)
∵
b= -2
6
| b-2 |.
∴| b-2 |=
| -2 -2 |
6
=| -4 |
6
=4-
6
16.计算:
解:(1)
(1)
3
2
×
16
+
1
3
×
144
-
1000
3
原式=
3
2
×4
+
1
3
×12
-10
=6+4-10
=0
(2)
8
- 4
=7
+3
(2)原式=
17.若实数a、b在数轴上的位置如图所示,
化简
0
a
b
| a-b|
-
|a|.
解:
∴a<0,
∴b>0,
∴a-b<0,
∴| a-b|
-
|a|=
b-a
-(a)
=b.
∵点a在数轴原点的左边,
∵点b在数轴原点的右边,
今天作业
课本P19页第2、10题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 七年级下册
第6章 实数 复习课件
乘方
开方
平方根
立方根
实数
有理数
无理数
互为逆运算
开平方
开立方
本章主要知识点
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根,这就是说,如果x2=a,那么x叫做a的平方根.
1.平方根定义
x= 中,a≥0, ≥0。
非负数a的平方根用符号“± ” 表示,读作:“正、负根号a”。
一般地,如果一个正数x 的平方等于a,即 x2=a,那么这个正数x 叫做a的算术平方根.
a的算术平方根记为:
读作:“根号a”, a叫做被开方数.
2.算术平方根
规定:0 的算术平方根是 0.
也就是说,负数不存在算术平方根。
正数有两个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根.
3.平方根的性质:
4.平方根的记法:
(1) 表示非负数a的正的平方根,
- 表示非负数a的负的平方根;
(2)± 表示非负数a的平方根,
与 - 互为相反数;
(3) 在± 中,a≥0。
一般地,如果一个数的立方等于 a,那么这个数就叫做 a 的立方根或三次方根。即:如果 x3 = a,那么x叫做 a 的立方根.
33 =27,所以3是27的立方根.
5.立方根的定义:
如果 x3 = a ,则 x 叫做 a 的立方根。
记作:x= , 读作“三次根号a”.
6.立方根的性质:
注意: (1)任何数的立方根有且只有一个; (2)一个数a与 同号; (3)互为相反数的两个数的立方根也互为相反数。
a>0,则 >0
a<0,则 <0;
a=0,则 =0。
正数的立方根是正数;
负数的立方根是负数;
0的立方根是0。
算术平方根、平方根、立方根联系和区别
算术平方根 平方根 立方根
表示方法
a的取值
性
质
开方
a≥0
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
是本身
0,1
0
0,1,-1
a≥0
a是任何数
a
a
3
a
±
7.实数的分类
实数
整数
分数
正整数
负整数
负分数
正分数
正无理数
负无理数
有限小数或循环小数
无限不循环小数
有理数
无理数
实数还可分为正实数、0、负实数。
无理数含3类:1.一般形式;2.特殊结构;3.特定含义
0
(一)算术平方根、平方根、立方根典型例析
例1.已知2m -1的平方根是±3,3m+n-1的算术平方根是4,求n-2m的立方根.
∵2m-1的平方根是± 3,
解:
而9的平方根是± 3,
∴2m-1=9,
∴m=5.
∵3m+n-1的算术平方根是4,
而16的算术平方根是4,
∴3m+n-1=16,
∴3×5+n-1=16,
∴n=2
∴n-2m=2-2×5
=-8
∵-8的立方根是-2,
∴n-2m的立方根为-2.
例2.已知: 2m-1 + m+7 =0,
求-2m的平方根.
3
3
∵ 互为相反数的和为0,
∴2m-1 + m+7 =0.
∴m=-2.
∴-2m=4.
∵4平方根是± 2,
∴-2m的平方根为±2.
解:
(二)实数相关概念典型例析
例1.已知下列各数:①- ,② ,
③ ,④ 3.14 ,⑤- ,⑥ ,⑦ ,⑧ ,⑨ .其中是无理数的是 .( 填写序号 )
3
5
π
3
1
16
2
-1
3
2
8
22
7
4
-1
| |
②
③
⑥
⑦
例2.比较 与 大小:
解:
3
5
2
5
-
1
3
5
>
∴
2
5
-
1
解法一,作差法
∵125>121,
∴
125
121,
>
∴5
5
11,
>
∴5
5
-11 ,
>0
2
5
-
1
∴
-
3
5
=
10
-
6
10
5
5
-5
=
10
5
5
-11
>0
例2.比较 与 大小:
解:
3
5
2
2.236
-
1
2
5
-
1
≈
≈0.618
3
5
=0.6
2
5
-
1
3
5
>
∴
2
5
-
1
解法二,利用计算器
例3.已知 的整数部分为a,小数部分为b.
求代数式a2-a-b的值.
13
解:
∵
13
3<
<4,
∴a=3,
b= -3
13
∴a2-a-b=
32
-3
-(
13
-3)
=9
-3
13
+3
-
=9-
13
(三)实数的运算典型例析
计算:(1) 3
2
(精确到0.01);
+
5
-
1
2
π
解:
原式≈
3×1.414
+2.236
- ×3.142
1
2
=4.242
+2.236
-1.571
=4.907
≈4.91
(注意:取无理数的近似值时,一般要比要求的精确度多取一位小数)
(三)实数的运算典型例析
计算:(2) -
49
+
2
1
4
64
3
+
解:
原式=
-7
+
3
2
+
4
=
-
3
2
已知
+ =0,
a+b-3
2a-b+6
求 a,b 的值.
(四)实数的非负性典型例析
解:
∵
+ =0,
a+b-3
2a-b+6
∴
2a-b+6=0
a+b-3=0
∴
2a-b=-6
a+b=3
∴
b=4
a=-1
64
±8
8
-4
3.
2.
1.
5.
6.
如果一个数的平方根为a+1和2a-7,
这个数为 .
9
4.
知识点过关练习
A .无限小数是无理数 ;
B .绝对值等于本身的数是正数;
C .实数和数轴上的点一一对应;
D .带根号的数是无理数.
7.下列叙述正确的是( )
C
8.下列说法中,错误的个数是 ( )
①无理数都是无限小数;
②无理数都是开方开不尽的数;
③带根号的都是无理数;
④无限小数都是无理数。
A.1个 B.2个 C.3个 D.4个
C
9.已知按规律排列的一列数: , , , ,
, , …,那么第6个数是 ,
在前6个数中,无理数共有 个
3
6
9
12
15
5
10.适合- < a<
的整数有 .
6
18
5
-2,-1,0,1,2
11.小明编写了一个程序:
输入x →x2 →立方根 → 倒数→
算术平方根 → ,则x为 .
1
2
12.若n= -6,则估计的值所在范围,
下列最接近的是( ).
8
A.4<
<5
n
B.3<
<4
n
C.2<
<3
n
D.1<
<2
n
59
D
13.已知正实数a的平方根是2m+3和n-4,且m-2n=3.求m的值.
正实数a的平方根是2m+3和n-4
解:
∴2m+3+n-4=0
∴2m+n=1
∴
m-2n=3
2m+n=1
∴
m=1
14.已知a是最大的负整数,b是 的小数部分,
c是 的相反数,d没有倒数.
求 的值.
3
2022
3
| a-b |+-
3
2
cd
解:
∵a是最大的负整数,
∴a= -1,
∵b是 的小数部分,
∵c是 的相反数,
∵d没有倒数,
∴c=- ,
∴d=0 .
∴| a-b |+ cd
3
2
∴b= -1,
3
2022
3
2022
3
|-1-( -1)|+ ×(- )×0
3
2
=
2022
3
3
3
=
3
15.设2 + 的整数部分为a,小数部分为b.
(1)求2a+1的平方根;(2)化简:
6
解:(1)
∵
6
2<
<3,
∴a=4,
b= -2
6
| b-2 |.
∴2 +2
<
2+
6
<3+2
∴4<
2+
6
<5
∴2a+1=2 ×4 +1
=9
∵9平方根是±3,
∴2a+1的平方根是±3.
15.设2 + 的整数部分为a,小数部分为b.
(1)求2a+1的平方根;(2)化简:
6
解:(2)
∵
b= -2
6
| b-2 |.
∴| b-2 |=
| -2 -2 |
6
=| -4 |
6
=4-
6
16.计算:
解:(1)
(1)
3
2
×
16
+
1
3
×
144
-
1000
3
原式=
3
2
×4
+
1
3
×12
-10
=6+4-10
=0
(2)
8
- 4
=7
+3
(2)原式=
17.若实数a、b在数轴上的位置如图所示,
化简
0
a
b
| a-b|
-
|a|.
解:
∴a<0,
∴b>0,
∴a-b<0,
∴| a-b|
-
|a|=
b-a
-(a)
=b.
∵点a在数轴原点的左边,
∵点b在数轴原点的右边,
今天作业
课本P19页第2、10题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
