冀教版数学七年级下册 11.3 公式法 课件(共19张PPT)
文档属性
| 名称 | 冀教版数学七年级下册 11.3 公式法 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 767.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
公式法
运用公式法
把乘法公式反过来用,可以把符合公式
特点的多项式因式分解,这种方法叫公式法.
(1)平方差公式:a2-b2=(a+b)(a-b)
(2)完全平方公式:
a2+2ab+b2=(a+b)2 a2-2ab+b2=(a-b)2
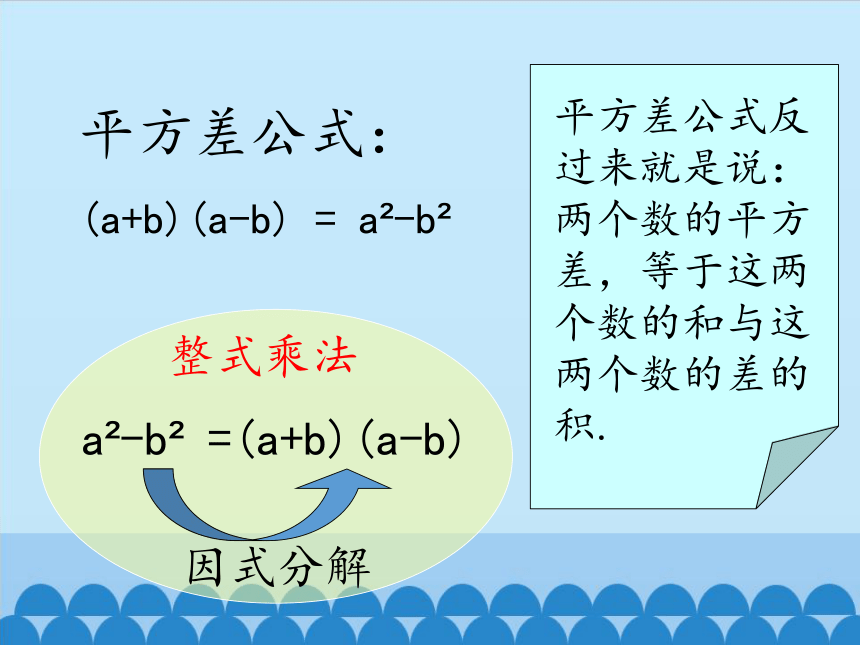
平方差公式反过来就是说:两个数的平方差,等于这两个数的和与这两个数的差的积.
a -b =(a+b)(a-b)
因式分解
平方差公式:
(a+b)(a-b) = a -b
整式乘法
将下面的多项式分解因式
1)m -16 2)4x -9y
m -16= m -4 =(m+4)(m-4)
a -b =(a+b)(a-b)
4x -9y =(2x) -(3y) =(2x+3y)(2x-3y)
(1)4x2-9y2; (2)(3m-1)2-9.
解:(1)4x2-9y2
=(2x)2-(3y)2
=(2x+3y)(2x-3y).
例1 把下列各式分解因式:
(2)(3m-1)2-9
=(3m-1)2-32
=(3m-1+3)(3m-1-3)
=(3m+2)(3m-4).
(1)a3-16a; (2)2ab3-2ab.
解:(1)a3-16a
=a(a2-16)
=a(a+4)(a-4).
例2 把下列各式分解因式:
(2)2ab3-2ab
=2ab(b2-1)
=2ab(b+1)(b-1).
巩固练习:
1.选择题:
(1)下列各式能用平方差公式分解因式的是( ).
4x +y B.4x-(-y) C.-4x -y D.-x +y
(2)-4a +1分解因式的结果应是 ( ).
-(4a+1)(4a-1) B.-(2a-1)(2a-1)
-(2a+1)(2a+1) D.-(2a+1)(2a-1)
2. 把下列各式分解因式:
1)18-2b 2)x4–1
D
D
解(1)原式=2(3+b)(3-b)
(2)原式=(x +1)(x+1)(x-1)
完全平方公式
现在我们把这个公式反过来
很显然,我们可以运用以上这个公式来分解因式了,我们把它称为“完全平方公式”.
我们把以上两个式子叫做完全平方式.
“头” 平方, “尾” 平方, “头” “尾”两倍中间放.
(1)t2+22t+121;
解:(1)t2+22t+121
=t2+2×11t+112
=(t+11)2.
例3 把下列各式分解因式:
(2)学生尝试解答
(1)ax2+2a2x+a3; (2)(x+y)2-4(x+y)+4;
解:(1)ax2+2a2x+a3
=a(x2+2ax+a2)
=a(x+a)2.
例4 把下列各式分解因式:
解:(2)(x+y)2-4(x+y)+4
=(x+y)2·2(x+y)·2+22
=(x+y-2)2.
判别下列各式是不是完全平方式.
是
是
是
是
完全平方式的特点:
1、必须是三项式
2、有两个平方的“项”
3、有这两平方“项”底数的2倍或-2倍
请补上一项,使下列多项式成为
完全平方式.
我们可以通过以上公式把“完全平方式”分解因式.
我们称之为:运用完全平方公式分解因式.
把下列式子分解因式
4x2+12xy+9y2
=(首±尾)2
b
a
将一个正方形的一角剪去一个小正方形,观察剪剩下的部分,你能在只能剪一刀的情况下,将剩余部分重新拼接成一个特殊四边形吗?
动手实践
=
a2-b2
(a+b)(a-b)
谢 谢
公式法
运用公式法
把乘法公式反过来用,可以把符合公式
特点的多项式因式分解,这种方法叫公式法.
(1)平方差公式:a2-b2=(a+b)(a-b)
(2)完全平方公式:
a2+2ab+b2=(a+b)2 a2-2ab+b2=(a-b)2
平方差公式反过来就是说:两个数的平方差,等于这两个数的和与这两个数的差的积.
a -b =(a+b)(a-b)
因式分解
平方差公式:
(a+b)(a-b) = a -b
整式乘法
将下面的多项式分解因式
1)m -16 2)4x -9y
m -16= m -4 =(m+4)(m-4)
a -b =(a+b)(a-b)
4x -9y =(2x) -(3y) =(2x+3y)(2x-3y)
(1)4x2-9y2; (2)(3m-1)2-9.
解:(1)4x2-9y2
=(2x)2-(3y)2
=(2x+3y)(2x-3y).
例1 把下列各式分解因式:
(2)(3m-1)2-9
=(3m-1)2-32
=(3m-1+3)(3m-1-3)
=(3m+2)(3m-4).
(1)a3-16a; (2)2ab3-2ab.
解:(1)a3-16a
=a(a2-16)
=a(a+4)(a-4).
例2 把下列各式分解因式:
(2)2ab3-2ab
=2ab(b2-1)
=2ab(b+1)(b-1).
巩固练习:
1.选择题:
(1)下列各式能用平方差公式分解因式的是( ).
4x +y B.4x-(-y) C.-4x -y D.-x +y
(2)-4a +1分解因式的结果应是 ( ).
-(4a+1)(4a-1) B.-(2a-1)(2a-1)
-(2a+1)(2a+1) D.-(2a+1)(2a-1)
2. 把下列各式分解因式:
1)18-2b 2)x4–1
D
D
解(1)原式=2(3+b)(3-b)
(2)原式=(x +1)(x+1)(x-1)
完全平方公式
现在我们把这个公式反过来
很显然,我们可以运用以上这个公式来分解因式了,我们把它称为“完全平方公式”.
我们把以上两个式子叫做完全平方式.
“头” 平方, “尾” 平方, “头” “尾”两倍中间放.
(1)t2+22t+121;
解:(1)t2+22t+121
=t2+2×11t+112
=(t+11)2.
例3 把下列各式分解因式:
(2)学生尝试解答
(1)ax2+2a2x+a3; (2)(x+y)2-4(x+y)+4;
解:(1)ax2+2a2x+a3
=a(x2+2ax+a2)
=a(x+a)2.
例4 把下列各式分解因式:
解:(2)(x+y)2-4(x+y)+4
=(x+y)2·2(x+y)·2+22
=(x+y-2)2.
判别下列各式是不是完全平方式.
是
是
是
是
完全平方式的特点:
1、必须是三项式
2、有两个平方的“项”
3、有这两平方“项”底数的2倍或-2倍
请补上一项,使下列多项式成为
完全平方式.
我们可以通过以上公式把“完全平方式”分解因式.
我们称之为:运用完全平方公式分解因式.
把下列式子分解因式
4x2+12xy+9y2
=(首±尾)2
b
a
将一个正方形的一角剪去一个小正方形,观察剪剩下的部分,你能在只能剪一刀的情况下,将剩余部分重新拼接成一个特殊四边形吗?
动手实践
=
a2-b2
(a+b)(a-b)
谢 谢
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
