勾股定理教案
图片预览
文档简介
勾股定理(一)导学案
一、学习目标:
1、了解多种拼图方法,验证勾股定理,感受解决同一个问题方法的多样性。
2、通过实例进一步了解勾股定理,应用勾股定理进行简单的计算和证明。,
3、进一步体会数形结合的思想以及数学知识之间内在联系。
二、学习重点:
通过自主学习验证归纳勾股定理。并进行应用。
三、学习过程:
(一)、学前准备:
1、每位同学准备四个全等的直角三角形。
2、查阅资料,网络搜索有关勾股定理的知识。
3、自主阅读课本本节内容。
(二)、自学、合作探究:
活动一:各小组成员选择自己最喜欢的拼图方法,验证勾股定理,
活动二:各小组派代表上来展示自己的拼图,并说出它的特点。
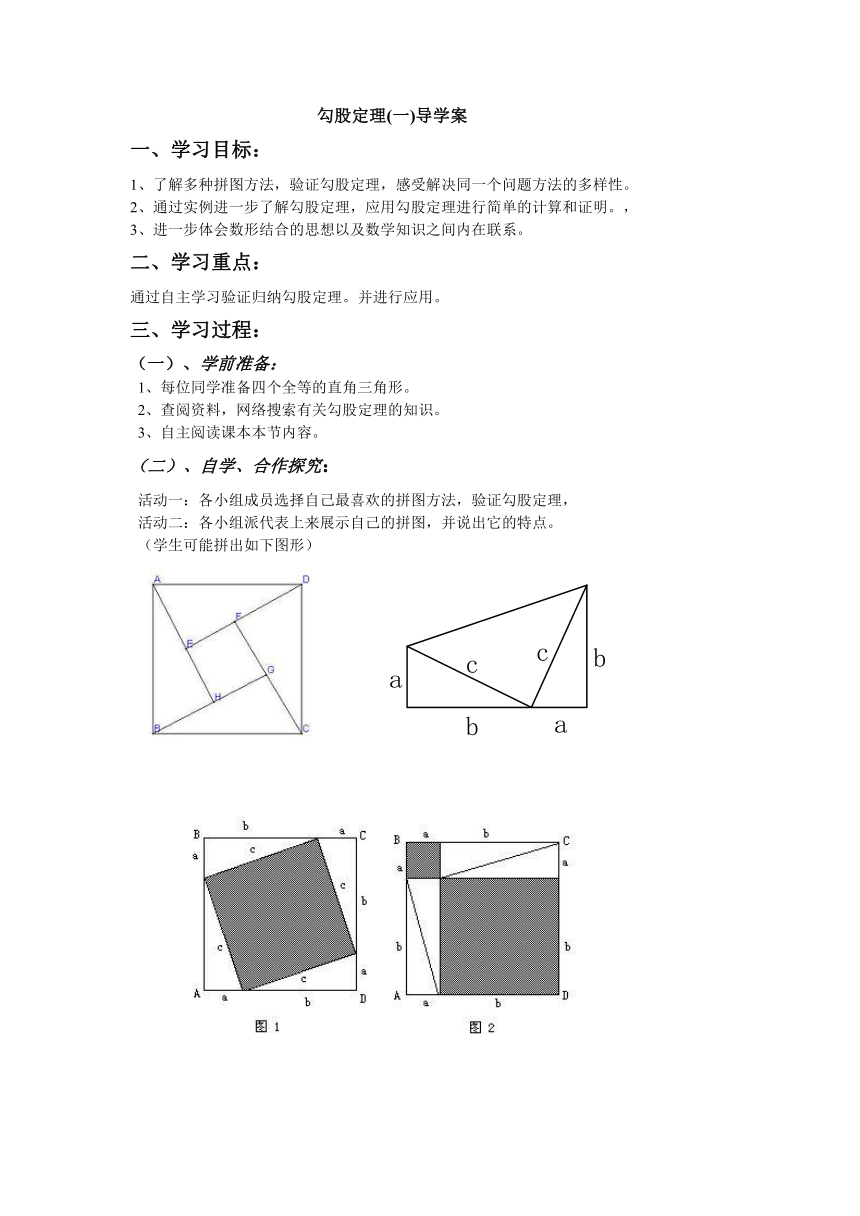
(学生可能拼出如下图形)
活动三、从你所拼的图形的面积构造等式验证勾股定理
看是否能得出 :c2=a2+b2
每一小组选一种图形写出验证的过程,小组间进行交流。
(三).归纳定理:
① 用语言表达勾股定理
② 用式子表达勾股定理
③ 运用勾股定理时该注意些什么
(四).定理应用:
例 1、在Rt△ABC中,∠C=90°
(1)若a=5,b=12,则c=________;
(2)b=8,c=17,则S△ABC=________。
(提示先构好图)
例2、下列各图中所示的线段的长度或正方形的面积为多少。(注:下列各图中的三角形均为直角三角形)
提示:正方形是以直角三角形的一边作为边,故面积可表达为
例3、如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
提示:
① AD 与BD有何关系?
② 设CD=x,则AD=
③ 在△ACD中根据勾股定理可列出
构造方程来解。
(五)课堂小结:
⑴ 我们通过什么方法来推导勾股定理的?
⑵ 拼图法证明勾股定理用了什么数学思想?
⑶ 勾股定理可以用来解决那些问题?
(六) 作业布置 :
课本习题:(2),(3),(4),(5).
一、学习目标:
1、了解多种拼图方法,验证勾股定理,感受解决同一个问题方法的多样性。
2、通过实例进一步了解勾股定理,应用勾股定理进行简单的计算和证明。,
3、进一步体会数形结合的思想以及数学知识之间内在联系。
二、学习重点:
通过自主学习验证归纳勾股定理。并进行应用。
三、学习过程:
(一)、学前准备:
1、每位同学准备四个全等的直角三角形。
2、查阅资料,网络搜索有关勾股定理的知识。
3、自主阅读课本本节内容。
(二)、自学、合作探究:
活动一:各小组成员选择自己最喜欢的拼图方法,验证勾股定理,
活动二:各小组派代表上来展示自己的拼图,并说出它的特点。
(学生可能拼出如下图形)
活动三、从你所拼的图形的面积构造等式验证勾股定理
看是否能得出 :c2=a2+b2
每一小组选一种图形写出验证的过程,小组间进行交流。
(三).归纳定理:
① 用语言表达勾股定理
② 用式子表达勾股定理
③ 运用勾股定理时该注意些什么
(四).定理应用:
例 1、在Rt△ABC中,∠C=90°
(1)若a=5,b=12,则c=________;
(2)b=8,c=17,则S△ABC=________。
(提示先构好图)
例2、下列各图中所示的线段的长度或正方形的面积为多少。(注:下列各图中的三角形均为直角三角形)
提示:正方形是以直角三角形的一边作为边,故面积可表达为
例3、如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
提示:
① AD 与BD有何关系?
② 设CD=x,则AD=
③ 在△ACD中根据勾股定理可列出
构造方程来解。
(五)课堂小结:
⑴ 我们通过什么方法来推导勾股定理的?
⑵ 拼图法证明勾股定理用了什么数学思想?
⑶ 勾股定理可以用来解决那些问题?
(六) 作业布置 :
课本习题:(2),(3),(4),(5).
