第18章勾股定理 复习课件(共23张PPT)
文档属性
| 名称 | 第18章勾股定理 复习课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 17:58:20 | ||
图片预览





文档简介
(共23张PPT)
第18章 勾股定理 复习课件
沪科版 八年级下册
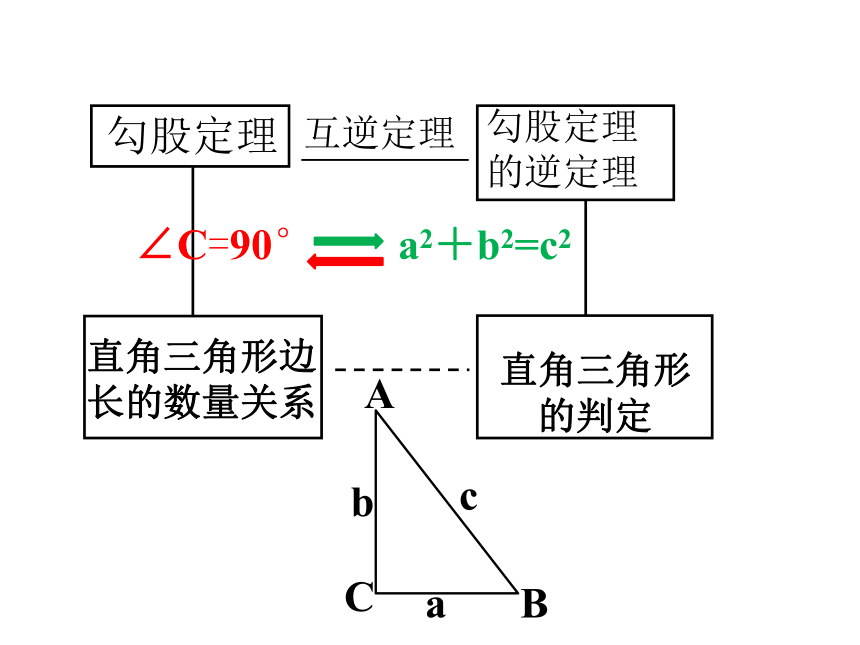
a2+b2=c2
勾股定理
直角三角形边
长的数量关系
勾股定理
的逆定理
直角三角形
的判定
互逆定理
∠C=90°
a
b
c
A
B
C
勾股定理的逆定理:
如果三角形的三边长a,b,c 满足
a2+b2= c2,那么这个三角形是直角三角形.
勾股定理:
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
b2-a2
1.如图,已知在△ABC 中,∠B=90°,一直角边为a,斜边为b,则另一直角边c满足c2 = .
为什么不是 ?
第一组练习: 勾股定理的直接应用
(一)知两边或一边一角型
a
b
c
A
C
B
c2=a2+b2
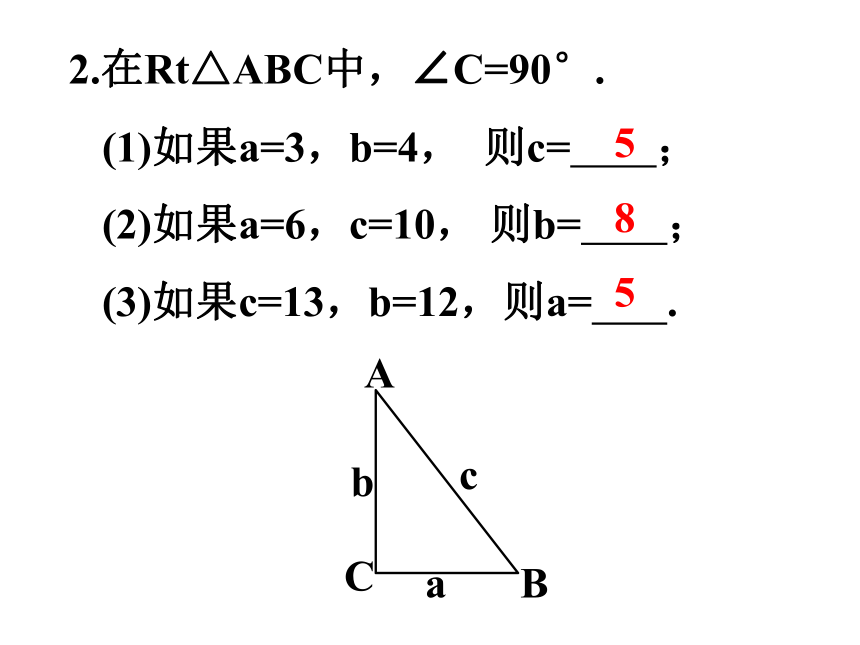
2.在Rt△ABC中,∠C=90°.
(1)如果a=3,b=4, 则c= ;
(2)如果a=6,c=10, 则b= ;
(3)如果c=13,b=12,则a= .
5
8
5
a
b
c
A
B
C
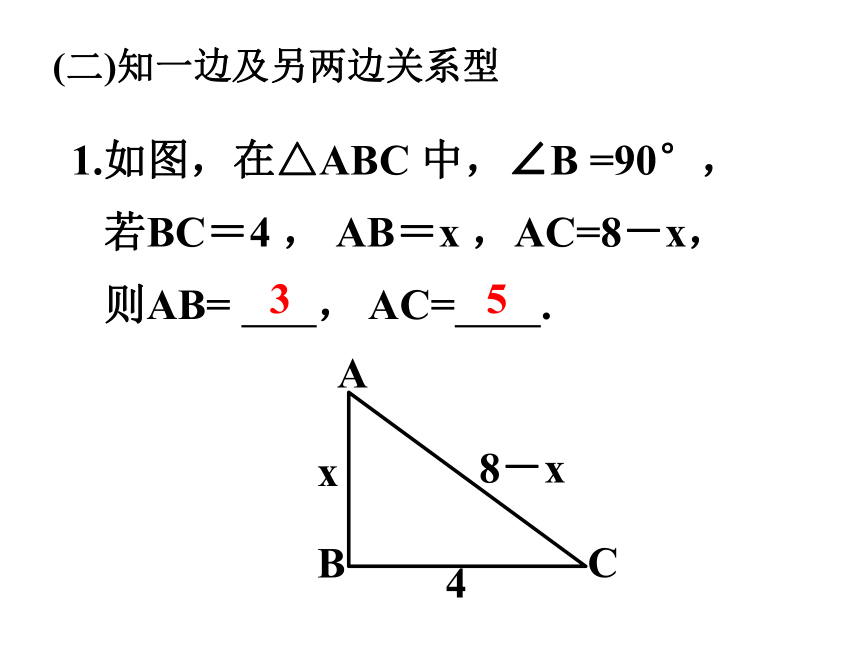
1.如图,在△ABC 中,∠B =90°,
若BC=4 , AB=x ,AC=8-x,
则AB= , AC= .
(二)知一边及另两边关系型
4
x
8-x
A
B
C
3
5
2.在Rt△ABC 中,∠B=90°,b=34,
a:c=8:15,则a= , c = .
(二)知一边及另两边关系型
16
30
∴(8x)2+(15x)2=342
设a=8x,
则c=15x.
∴ 64x2+225x2=(17×2)2
∴ x2=22
∴ 289x2=(17×2)2
∴ x=±2
∴ 8x=16.
∴(17)2x2=172×22
解:
∵a2+c2=b2
(注意那条边是斜边)
(三)分类讨论的题型
1. 对三角形边的分类.
1.一个直角三角形的两边长分别为4、5,
那么第三条边长为 .
3
41
或
注意:边长5可能是斜边,也可能是直角边
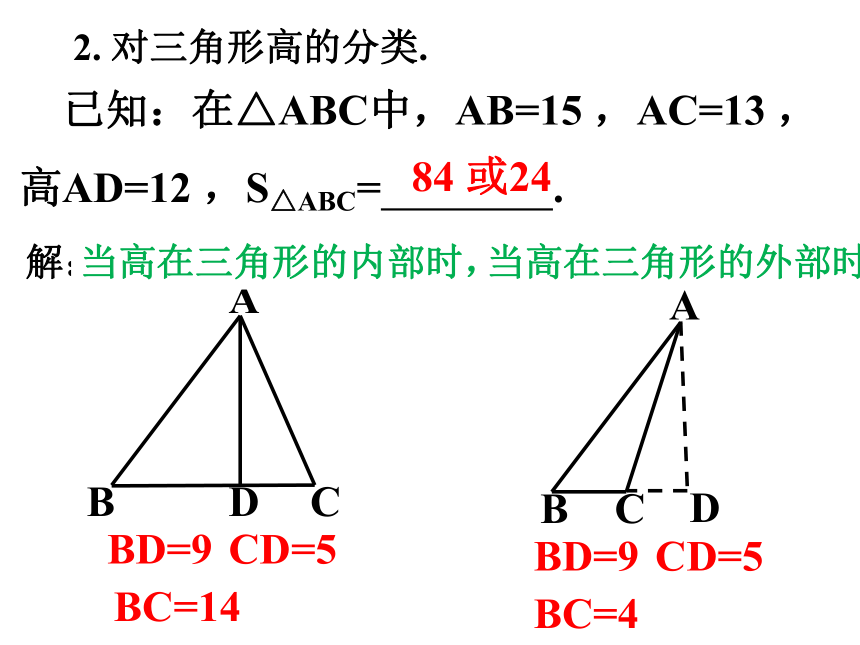
已知:在△ABC中,AB=15 ,AC=13 ,高AD=12 ,S△ABC= .
2. 对三角形高的分类.
A
B
D
C
A
B
C
或24
84
D
BD=9
CD=5
BC=4
BD=9
CD=5
BC=14
解:
当高在三角形的内部时,
当高在三角形的外部时,
1.在一块平地上,张大爷家屋前9米远处有一棵大树.在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米.出门在外的张大爷担心自己的房子被倒下的大树砸到.大树倒下时能砸到张大爷的房子吗?( )
A.一定不会 B.可能会
C.一定会 D.以上答案都不对
第二组练习: 用勾股定理解决简单的实际问题
A
2.小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多1 m,当他把绳子的下端拉开5 m后,发现下端刚好接触地面,则旗杆的高为( ).
A.8 m B.10 m C.12 m D.14 m
C
5
1
x+1
x
设旗杆的高为xm
3.如图, 楼梯的高度为2m,楼梯坡面的长度为4m,要在楼梯的表面铺上地毯,那么地毯的长度至少需要多少米?
地毯的长度为
BC
+AC
B
A
C
分析:
3.如图, 楼梯的高度为2m,楼梯坡面的长度为4m,要在楼梯的表面铺上地毯,那么地毯的长度至少需要多少米?
B
A
C
∴BC+AC=
解:
在Rt△ABC中,
AC2=AB2-BC2
=42-22=12.
∴AC=
12
=
3
2
2+
3
2
=2+2 × 1.73
≈5.5(m)
答:地毯的长度至少需要5.5米.
1.证明线段相等.
已知:如图,AD是△ABC的高AB=10,AD=8,BC=12 . 求证: △ABC是等腰三角形.
第三组练习: 会用勾股定理解决较综合的问题
A
B
D
C
∵BD2=AB2-AD2
证明:
Rt△ABC 中,
=102-82=62
∴BD=6,
∵BC=12,
∴DC=BC-BD=12-10=6
∴BD=CD.
∴AB=AC,
∵AD⊥BC,
∴△ABC是等腰三角形.
2.解决折叠的问题.
已知:如图,将长方形的一边BC沿CE折叠,使得点B落在AD边的点F处,若AB=8,BC=10, 求BE的长.
B
C
D
A
E
F
由折叠的性质可知△EBC≌EFC,
∴FC=BC=10,
∵四边形ABCD是长方形,
∴∠D=90°,
∵CD=8,
∴DF2=CF2-CD2
=102-82
∴DF=6.
解:
=62
BE=EF.
B
C
D
A
E
F
x
x
4
8-x
由折叠的性质可知△EBC≌EFC,
∴FC=BC=10,
∵四边形ABCD是长方形,
∴∠D=90°,
∵CD=8,
∴DF2=CF2-CD2
=102-82
∴DF=6.
解:
∴AF=AD-DF=4,
设BE=x,则EF=
BE=x,
∴AE=AB-BE=8-x,
解得:x=5,
∴线段BE的长度是5.
∵EF2=AF2+AE2,
∴x2=42+(8-x)2,
=62
BE=EF.
3.做高线,构造直角三角形.
已知:如图,在△ABC中,∠B=45°,∠C=60°,AB=6.则BC 的长为 .
A
B
C
D
6
∴(2CD)2=AD2+CD2,
∴AD=BD,
∵AD⊥BC,
∠B=45°,
∴∠BAD=45°,
∴∠BAD=∠B,
∴2AD2=2BD2=62
∴AD=BD
2
=3
∵AD⊥BC,
∠C=60°,
∴∠CAD=30°,
∴AC=CD,
∵AB2=AD2+BD2,
∴CD= .
6
2
3
6
+
解:
1.分别以下列四组数为一个三角形的边长:
①3,4,5; ②5,12,13;
③8,15,17; ④4,5,6.
其中能构成直角三角形的有 .
①
②
③
第四组练习: 勾股定理及其逆定理的综合应用
2.正方形ABCD的边长AB=10.点E在正方形ABCD内,且AE=6,BE=8,则阴影部分的面积是( ).
A.48 B.60 C.76 D.80
A
B
C
D
E
C
3.已知:如图,四边形ABCD,AB=1,BC=2,CD=2,AD=3,且AB⊥BC.求四边形ABCD的面积.
A
B
C
D
1
2
5
2
3
=1
5
+
∵AB⊥BC,
∴∠ABC=90°,
∴AC2=AB2+BC2
=12+22
=5
∴AC=
5
∵AC2+CD2=
5+22
=9
=32
=AD2
∴∠ACD=90°,
∴SABCD
=S△ABC+S△ACD
解:
=
1
2
AB·BC
+
1
2
AC·CD
今天作业
课本P136页第9、10题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第18章 勾股定理 复习课件
沪科版 八年级下册
a2+b2=c2
勾股定理
直角三角形边
长的数量关系
勾股定理
的逆定理
直角三角形
的判定
互逆定理
∠C=90°
a
b
c
A
B
C
勾股定理的逆定理:
如果三角形的三边长a,b,c 满足
a2+b2= c2,那么这个三角形是直角三角形.
勾股定理:
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
b2-a2
1.如图,已知在△ABC 中,∠B=90°,一直角边为a,斜边为b,则另一直角边c满足c2 = .
为什么不是 ?
第一组练习: 勾股定理的直接应用
(一)知两边或一边一角型
a
b
c
A
C
B
c2=a2+b2
2.在Rt△ABC中,∠C=90°.
(1)如果a=3,b=4, 则c= ;
(2)如果a=6,c=10, 则b= ;
(3)如果c=13,b=12,则a= .
5
8
5
a
b
c
A
B
C
1.如图,在△ABC 中,∠B =90°,
若BC=4 , AB=x ,AC=8-x,
则AB= , AC= .
(二)知一边及另两边关系型
4
x
8-x
A
B
C
3
5
2.在Rt△ABC 中,∠B=90°,b=34,
a:c=8:15,则a= , c = .
(二)知一边及另两边关系型
16
30
∴(8x)2+(15x)2=342
设a=8x,
则c=15x.
∴ 64x2+225x2=(17×2)2
∴ x2=22
∴ 289x2=(17×2)2
∴ x=±2
∴ 8x=16.
∴(17)2x2=172×22
解:
∵a2+c2=b2
(注意那条边是斜边)
(三)分类讨论的题型
1. 对三角形边的分类.
1.一个直角三角形的两边长分别为4、5,
那么第三条边长为 .
3
41
或
注意:边长5可能是斜边,也可能是直角边
已知:在△ABC中,AB=15 ,AC=13 ,高AD=12 ,S△ABC= .
2. 对三角形高的分类.
A
B
D
C
A
B
C
或24
84
D
BD=9
CD=5
BC=4
BD=9
CD=5
BC=14
解:
当高在三角形的内部时,
当高在三角形的外部时,
1.在一块平地上,张大爷家屋前9米远处有一棵大树.在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米.出门在外的张大爷担心自己的房子被倒下的大树砸到.大树倒下时能砸到张大爷的房子吗?( )
A.一定不会 B.可能会
C.一定会 D.以上答案都不对
第二组练习: 用勾股定理解决简单的实际问题
A
2.小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多1 m,当他把绳子的下端拉开5 m后,发现下端刚好接触地面,则旗杆的高为( ).
A.8 m B.10 m C.12 m D.14 m
C
5
1
x+1
x
设旗杆的高为xm
3.如图, 楼梯的高度为2m,楼梯坡面的长度为4m,要在楼梯的表面铺上地毯,那么地毯的长度至少需要多少米?
地毯的长度为
BC
+AC
B
A
C
分析:
3.如图, 楼梯的高度为2m,楼梯坡面的长度为4m,要在楼梯的表面铺上地毯,那么地毯的长度至少需要多少米?
B
A
C
∴BC+AC=
解:
在Rt△ABC中,
AC2=AB2-BC2
=42-22=12.
∴AC=
12
=
3
2
2+
3
2
=2+2 × 1.73
≈5.5(m)
答:地毯的长度至少需要5.5米.
1.证明线段相等.
已知:如图,AD是△ABC的高AB=10,AD=8,BC=12 . 求证: △ABC是等腰三角形.
第三组练习: 会用勾股定理解决较综合的问题
A
B
D
C
∵BD2=AB2-AD2
证明:
Rt△ABC 中,
=102-82=62
∴BD=6,
∵BC=12,
∴DC=BC-BD=12-10=6
∴BD=CD.
∴AB=AC,
∵AD⊥BC,
∴△ABC是等腰三角形.
2.解决折叠的问题.
已知:如图,将长方形的一边BC沿CE折叠,使得点B落在AD边的点F处,若AB=8,BC=10, 求BE的长.
B
C
D
A
E
F
由折叠的性质可知△EBC≌EFC,
∴FC=BC=10,
∵四边形ABCD是长方形,
∴∠D=90°,
∵CD=8,
∴DF2=CF2-CD2
=102-82
∴DF=6.
解:
=62
BE=EF.
B
C
D
A
E
F
x
x
4
8-x
由折叠的性质可知△EBC≌EFC,
∴FC=BC=10,
∵四边形ABCD是长方形,
∴∠D=90°,
∵CD=8,
∴DF2=CF2-CD2
=102-82
∴DF=6.
解:
∴AF=AD-DF=4,
设BE=x,则EF=
BE=x,
∴AE=AB-BE=8-x,
解得:x=5,
∴线段BE的长度是5.
∵EF2=AF2+AE2,
∴x2=42+(8-x)2,
=62
BE=EF.
3.做高线,构造直角三角形.
已知:如图,在△ABC中,∠B=45°,∠C=60°,AB=6.则BC 的长为 .
A
B
C
D
6
∴(2CD)2=AD2+CD2,
∴AD=BD,
∵AD⊥BC,
∠B=45°,
∴∠BAD=45°,
∴∠BAD=∠B,
∴2AD2=2BD2=62
∴AD=BD
2
=3
∵AD⊥BC,
∠C=60°,
∴∠CAD=30°,
∴AC=CD,
∵AB2=AD2+BD2,
∴CD= .
6
2
3
6
+
解:
1.分别以下列四组数为一个三角形的边长:
①3,4,5; ②5,12,13;
③8,15,17; ④4,5,6.
其中能构成直角三角形的有 .
①
②
③
第四组练习: 勾股定理及其逆定理的综合应用
2.正方形ABCD的边长AB=10.点E在正方形ABCD内,且AE=6,BE=8,则阴影部分的面积是( ).
A.48 B.60 C.76 D.80
A
B
C
D
E
C
3.已知:如图,四边形ABCD,AB=1,BC=2,CD=2,AD=3,且AB⊥BC.求四边形ABCD的面积.
A
B
C
D
1
2
5
2
3
=1
5
+
∵AB⊥BC,
∴∠ABC=90°,
∴AC2=AB2+BC2
=12+22
=5
∴AC=
5
∵AC2+CD2=
5+22
=9
=32
=AD2
∴∠ACD=90°,
∴SABCD
=S△ABC+S△ACD
解:
=
1
2
AB·BC
+
1
2
AC·CD
今天作业
课本P136页第9、10题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
